Unitarity (physics)
Encyclopedia
In quantum physics, unitarity is a restriction on the allowed evolution of quantum systems that insures the sum of probabilities of all possible outcomes of any event is always 1.
More precisely, the operator which describes the progress of a physical system in time must be a unitary operator
. When the Hamiltonian
is time-independent the unitary operator is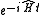 .
.
Similarly, the S-matrix that describes how the physical system changes in a scattering
process must be a unitary operator
as well; this implies the optical theorem
.
In quantum field theory
one usually uses a mathematical description which includes unphysical fundamental particles, such as a longitudinal
photon
s. These particles must not appear as the end-states of a scattering
process. Unitarity of the S-matrix and the optical theorem
in particular implies that such unphysical particles must not appear as virtual particle
s in intermediate states. The mathematical machinery which is used to ensure this includes gauge symmetry and sometimes also Faddeev–Popov ghosts.
Since unitarity of a theory is necessary for its consistency, the term is sometimes also used as a synonym for consistency, and is sometimes used for other necessary conditions for consistency, in particular the condition that the Hamiltonian is bounded from below. This means that there is a state of minimal energy
(called the ground state
or vacuum state
). This is needed for the second law of thermodynamics
to hold.
In theoretical physics
, a unitarity bound is any inequality that follows from the unitarity of the evolution operator, i.e. from the statement that probabilities are numbers between 0 and 1 whose sum is conserved. Unitarity implies, among other things, the optical theorem
. According to the optical theorem, the imaginary part of a probability amplitude
Im(M) of a 2-body forward scattering is related to the total cross section
, up to some numerical factors. Because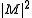 for the forward scattering process is one of the terms that contributes to the total cross section, it cannot exceed the total cross section i.e. Im(M). The inequality
for the forward scattering process is one of the terms that contributes to the total cross section, it cannot exceed the total cross section i.e. Im(M). The inequality
implies that the complex number
M must belong to a certain disk in the complex plane. Similar unitarity bounds imply that the amplitudes and cross section cannot increase too much with energy or they must decrease as quickly as a certain formula dictates.
More precisely, the operator which describes the progress of a physical system in time must be a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
. When the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is time-independent the unitary operator is
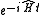 .
.Similarly, the S-matrix that describes how the physical system changes in a scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
process must be a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
as well; this implies the optical theorem
Optical theorem
In physics, the optical theorem is a general law of wave scattering theory, which relates the forward scattering amplitude to the total cross section of the scatterer...
.
In quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
one usually uses a mathematical description which includes unphysical fundamental particles, such as a longitudinal
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. These particles must not appear as the end-states of a scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
process. Unitarity of the S-matrix and the optical theorem
Optical theorem
In physics, the optical theorem is a general law of wave scattering theory, which relates the forward scattering amplitude to the total cross section of the scatterer...
in particular implies that such unphysical particles must not appear as virtual particle
Virtual particle
In physics, a virtual particle is a particle that exists for a limited time and space. The energy and momentum of a virtual particle are uncertain according to the uncertainty principle...
s in intermediate states. The mathematical machinery which is used to ensure this includes gauge symmetry and sometimes also Faddeev–Popov ghosts.
Since unitarity of a theory is necessary for its consistency, the term is sometimes also used as a synonym for consistency, and is sometimes used for other necessary conditions for consistency, in particular the condition that the Hamiltonian is bounded from below. This means that there is a state of minimal energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
(called the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
or vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
). This is needed for the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
to hold.
In theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, a unitarity bound is any inequality that follows from the unitarity of the evolution operator, i.e. from the statement that probabilities are numbers between 0 and 1 whose sum is conserved. Unitarity implies, among other things, the optical theorem
Optical theorem
In physics, the optical theorem is a general law of wave scattering theory, which relates the forward scattering amplitude to the total cross section of the scatterer...
. According to the optical theorem, the imaginary part of a probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
Im(M) of a 2-body forward scattering is related to the total cross section
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
, up to some numerical factors. Because
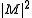 for the forward scattering process is one of the terms that contributes to the total cross section, it cannot exceed the total cross section i.e. Im(M). The inequality
for the forward scattering process is one of the terms that contributes to the total cross section, it cannot exceed the total cross section i.e. Im(M). The inequalityimplies that the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
M must belong to a certain disk in the complex plane. Similar unitarity bounds imply that the amplitudes and cross section cannot increase too much with energy or they must decrease as quickly as a certain formula dictates.
See also
- Stone's theorem on one-parameter unitary groupsStone's theorem on one-parameter unitary groupsIn mathematics, Stone's theorem on one-parameter unitary groups is a basic theorem of functional analysis which establishes a one-to-one correspondence between self-adjoint operators on a Hilbert space H and one-parameter families of unitary operators...
- Probability axiomsProbability axiomsIn probability theory, the probability P of some event E, denoted P, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov, which are described below....
- Antiunitary operator
- Wigner's theoremWigner's theoremWigner's theorem, proved by Eugene Wigner in 1931, is a cornerstone of the mathematical formulation of quantum mechanics. The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states....