
Uniform boundedness principle
Encyclopedia
In mathematics
, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis
. Together with the Hahn–Banach theorem
and the open mapping theorem
, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators (and thus bounded operators) whose domain is a Banach space
, pointwise boundedness is equivalent to uniform boundedness in operator norm.
The theorem was first published in 1927 by Stefan Banach
and Hugo Steinhaus
but it was also proven independently by Hans Hahn
.
Theorem. Let X be a Banach space
and Y be a normed vector space
. Suppose that F is a collection of continuous linear operators from X to Y.
The uniform boundedness principle states that if for all x in X we have
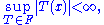
then
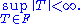
The completeness of X enables the following short proof, using the Baire category theorem
:
Proof.
A direct consequence is:
Corollary. If a sequence of bounded operators (Tn) converges pointwise, that is, lim Tn(x) exists for all x in X, then these pointwise limits define a bounded operator T.
Note it is not claimed above that Tn converges to T in operator norm, i.e. uniformly on bounded sets. (However, since {Tn} is bounded in operator norm, and the limit operator T is continuous, a standard "3-ε" estimate shows that Tn converges to T uniformly on compact sets.)
Another corollary is that any weakly bounded subset S in a normed space Y is bounded; indeed, the elements of S define a pointwise bounded family of continuous linear forms on the Banach space X = Y∗, continuous dual of Y. By the uniform boundedness principle, the norms of elements of S, as functionals on X, that is, norms in the second dual Y∗∗, are bounded. But for every s ∈ S, the norm in the second dual coincides with the norm in Y, by a consequence of the Hahn–Banach theorem
.
Let L(X, Y) denote the continuous operators from X to Y, with the operator norm. If the collection F is unbounded in L(X, Y), then by the uniform boundedness principle, the set
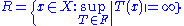
is not empty. In fact, it is dense in X. The complement of R in X is the countable union of closed sets ∪Xn. By the argument used in proving the theorem, each Xn is nowhere dense, i.e. the subset ∪Xn is of first category. Therefore R is the complement of a subset of first category in a Baire space. By definition of a Baire space, such sets (called residual sets) are dense. Such reasoning leads to the principle of condensation of singularities, which can be formulated as follows:
Theorem. Let X be a Banach space, {Yn} a sequence of normed vector spaces, and Fn a unbounded family in L(X, Yn). Then the set
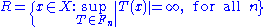
is dense in X.
Proof.
For ƒ in C(T), its Fourier series
is defined by
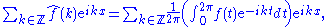
and the N-th symmetric partial sum is
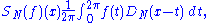
where DN is the N-th Dirichlet kernel. Fix x in T and consider the convergence of {SN(ƒ)(x)}. The functional φN, x : C(T) → C defined by
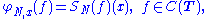
is bounded. The norm of φN, x, in the dual of C(T), is the norm of the signed measure (2π)−1DN(x−t) dt, namely
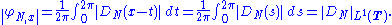
One can verify that

So the collection {φN, x} is unbounded in C(T)∗, the dual of C(T). Therefore by the uniform boundedness principle, for any x in T, the set of continuous functions whose Fourier series diverges at x is dense in C(T).
More can be concluded by applying the principle of condensation of singularities. Let {xm} be a dense sequence in T. Define
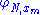
in the similar way as above. The principle of condensation of singularities then says that the set of continuous functions whose Fourier series diverges at each xm is dense in C(T) (however, the Fourier series of a continuous function ƒ converges to ƒ(x) for almost every x ∈ T, by Carleson's theorem
).
where the following generalized version of the theorem holds :
Alternatively, the statement also holds whenever X is a Baire space
and Y is a locally convex space .
proves a weaker form of this theorem with Fréchet space
s rather than the usual Banach spaces. Specifically,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. Together with the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
and the open mapping theorem
Open mapping theorem (functional analysis)
In functional analysis, the open mapping theorem, also known as the Banach–Schauder theorem , is a fundamental result which states that if a continuous linear operator between Banach spaces is surjective then it is an open map...
, it is considered one of the cornerstones of the field. In its basic form, it asserts that for a family of continuous linear operators (and thus bounded operators) whose domain is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, pointwise boundedness is equivalent to uniform boundedness in operator norm.
The theorem was first published in 1927 by Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
and Hugo Steinhaus
Hugo Steinhaus
Władysław Hugo Dionizy Steinhaus was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the University of Lwów, where he helped establish what later became known as the Lwów School of Mathematics...
but it was also proven independently by Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
.
Uniform boundedness principle
The precise statement of the result is:Theorem. Let X be a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
and Y be a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
. Suppose that F is a collection of continuous linear operators from X to Y.
The uniform boundedness principle states that if for all x in X we have
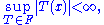
then
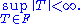
The completeness of X enables the following short proof, using the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
:
Proof.
- Define the closed sets Xn with n = 1, 2, 3, … by
- By hypothesis, the union of all the Xn is X. Since X is a Baire spaceBaire spaceIn mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
, one of the Xn, say Xm, has an interior point (Xn are closed sets), i.e., there exists a δ > 0 and a y in X such that all x ∈ X with ||x − y|| < δ are elements of Xm. Now, choose an arbitrary z in X with ||z|| < δ. Then, y and y + z are elements of Xm and hence, for every operator T in the family F, ||T(z)|| ≤ ||T(y + z)|| + ||T(y)|| ≤ m + m = 2m. Since z is arbitrary in the ball of radius δ, it follows that ||T|| ≤ 2m / δ for all T in F, which proves the theorem.
A direct consequence is:
Corollary. If a sequence of bounded operators (Tn) converges pointwise, that is, lim Tn(x) exists for all x in X, then these pointwise limits define a bounded operator T.
Note it is not claimed above that Tn converges to T in operator norm, i.e. uniformly on bounded sets. (However, since {Tn} is bounded in operator norm, and the limit operator T is continuous, a standard "3-ε" estimate shows that Tn converges to T uniformly on compact sets.)
Another corollary is that any weakly bounded subset S in a normed space Y is bounded; indeed, the elements of S define a pointwise bounded family of continuous linear forms on the Banach space X = Y∗, continuous dual of Y. By the uniform boundedness principle, the norms of elements of S, as functionals on X, that is, norms in the second dual Y∗∗, are bounded. But for every s ∈ S, the norm in the second dual coincides with the norm in Y, by a consequence of the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
.
Let L(X, Y) denote the continuous operators from X to Y, with the operator norm. If the collection F is unbounded in L(X, Y), then by the uniform boundedness principle, the set
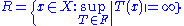
is not empty. In fact, it is dense in X. The complement of R in X is the countable union of closed sets ∪Xn. By the argument used in proving the theorem, each Xn is nowhere dense, i.e. the subset ∪Xn is of first category. Therefore R is the complement of a subset of first category in a Baire space. By definition of a Baire space, such sets (called residual sets) are dense. Such reasoning leads to the principle of condensation of singularities, which can be formulated as follows:
Theorem. Let X be a Banach space, {Yn} a sequence of normed vector spaces, and Fn a unbounded family in L(X, Yn). Then the set
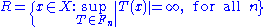
is dense in X.
Proof.
- The complement of R is the countable union
- of sets of first category. Therefore its residual set R is dense.
An example: pointwise convergence of Fourier series
Let T be the circle, and let C(T) be the Banach space of continuous functions on T, with the uniform norm. Using the uniform boundedness principle, one can show that the Fourier series, "typically", does not converge pointwise for elements in C(T).For ƒ in C(T), its Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
is defined by
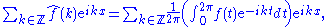
and the N-th symmetric partial sum is
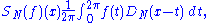
where DN is the N-th Dirichlet kernel. Fix x in T and consider the convergence of {SN(ƒ)(x)}. The functional φN, x : C(T) → C defined by
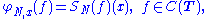
is bounded. The norm of φN, x, in the dual of C(T), is the norm of the signed measure (2π)−1DN(x−t) dt, namely
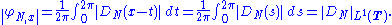
One can verify that

So the collection {φN, x} is unbounded in C(T)∗, the dual of C(T). Therefore by the uniform boundedness principle, for any x in T, the set of continuous functions whose Fourier series diverges at x is dense in C(T).
More can be concluded by applying the principle of condensation of singularities. Let {xm} be a dense sequence in T. Define
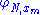
in the similar way as above. The principle of condensation of singularities then says that the set of continuous functions whose Fourier series diverges at each xm is dense in C(T) (however, the Fourier series of a continuous function ƒ converges to ƒ(x) for almost every x ∈ T, by Carleson's theorem
Carleson's theorem
Carleson's theorem is a fundamental result in mathematical analysis establishing the pointwise almost everywhere convergence of Fourier series of L2 functions, proved by...
).
Generalizations
The least restrictive setting for the uniform boundedness principle is a barrelled spaceBarrelled space
In functional analysis and related areas of mathematics, barrelled spaces are Hausdorff topological vector spaces for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set which is convex, balanced,...
where the following generalized version of the theorem holds :
- Given a barrelled space X and a locally convex space Y, then any family of pointwise bounded continuous linear mappings from X to Y is equicontinuous (even uniformly equicontinuous).
Alternatively, the statement also holds whenever X is a Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
and Y is a locally convex space .
proves a weaker form of this theorem with Fréchet space
Fréchet space
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s rather than the usual Banach spaces. Specifically,
- Let X be a Fréchet space, Y a normed space, and H a set of continuous linear mappings of X into Y. If
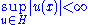 for every x∈X, then the family H is equicontinuous.
for every x∈X, then the family H is equicontinuous.
See also
- Barrelled spaceBarrelled spaceIn functional analysis and related areas of mathematics, barrelled spaces are Hausdorff topological vector spaces for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set which is convex, balanced,...
, a topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
with minimum requirements for the Banach Steinhaus theorem to hold



