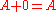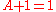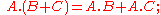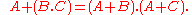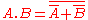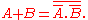Two-element Boolean algebra
Encyclopedia
In mathematics
and abstract algebra
, the two-element Boolean algebra is the Boolean algebra whose underlying set (or universe
or carrier) B is the Boolean domain
. The elements of the Boolean domain are 1 and 0 by convention, so that B = {0, 1}. Paul Halmos
's name for this algebra "2" has some following in the literature, and will be employed here.
.
An operation
of arity
n is a mapping
from Bn to B. Boolean algebra consists of two binary operation
s and unary
complementation. The binary operations have been named and notated in various ways. Here they are called 'sum' and 'product', and notated by infix '+' and '.', respectively. Sum and product commute
and associate
, as in the usual algebra of real numbers
. As for the order of operations
, brackets are decisive if present. Otherwise '.' precedes '+'. Hence A.B + C is parsed as (A.B) + C and not as A.(B + C). Complementation is denoted by writing an overbar over its argument. The numerical analog of the complement of X is 1 − X. In the language of universal algebra
, a Boolean algebra is a
algebra
of type
.
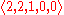Either one-to-one correspondence between {0,1} and {True,False} yields classical bivalent logic in equational form, with complementation read as NOT. If 1 is read as True, '+' is read as OR, and '.' as AND, and vice versa if 1 is read as False.
Note that:
This Boolean arithmetic suffices to verify any equation of 2, including the axioms, by examining every possible assignment of 0s and 1s to each variable (see decision procedure).
The following equations may now be verified:
Each of '+' and '.' distributes
over the other:
That '.' distributes over '+' agrees with elementary algebra
, but not '+' over '.'. For this and other reasons, a sum of products (leading to a NAND
synthesis) is more commonly employed than a product of sums (leading to a NOR
synthesis).
Each of '+' and '.' can be defined in terms of the other and complementation:
We only need one binary operation, and concatenation
suffices to denote it. Hence concatenation and overbar suffice to notate 2. This notation is also that of Quine
's Boolean term schemata. Letting (X) denote the complement of X and "" denote either 0 or 1 yields the syntax
of the primary algebra
.
A basis for 2 is a set of equations, called axiom
s, from which all of the above equations (and more) can be derived. There are many known bases for all Boolean algebras and hence for 2. An elegant basis notated using only concatenation and overbar is:
If 0=1, (1)-(3) are the axioms for an abelian group
.
(1) only serves to prove that concatenation commutes and associates. First assume that (1) associates from either the left or the right, then prove commutativity. Then prove association from the other direction. Associativity is simply association from the left and right combined.
This basis makes for an easy approach to proof, called calculation
, that proceeds by simplifying expressions to 0 or 1, by invoking axioms (2)–(4), and the elementary identities AA = A,
, 1+A = 1, and the distributive law.
the result is logically equivalent
to what you started with. Repeated application of De Morgan's theorem to parts of a function can be used to drive all complements down to the individual variables.
A powerful and nontrivial metatheorem
states that any theorem of 2 holds for all Boolean algebras. Conversely, an identity that holds for an arbitrary nontrivial Boolean algebra also holds in 2. Hence all the mathematical content of Boolean algebra is captured by 2. This theorem is useful because any equation in 2 can be verified by a decision procedure. Logicians refer to this fact as "2 is decidable
". All known decision procedures require a number of steps that is an exponential function
of the number of variables N appearing in the equation to be verified. Whether there exists a decision procedure whose steps are a polynomial function of N falls under the P = NP conjecture.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the two-element Boolean algebra is the Boolean algebra whose underlying set (or universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
or carrier) B is the Boolean domain
Boolean domain
In mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include false and true...
. The elements of the Boolean domain are 1 and 0 by convention, so that B = {0, 1}. Paul Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
's name for this algebra "2" has some following in the literature, and will be employed here.
Definition
B is a partially ordered set and the elements of B are also its boundsBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
.
An operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of arity
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
n is a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from Bn to B. Boolean algebra consists of two binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s and unary
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
complementation. The binary operations have been named and notated in various ways. Here they are called 'sum' and 'product', and notated by infix '+' and '.', respectively. Sum and product commute
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and associate
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, as in the usual algebra of real numbers
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
. As for the order of operations
Order of operations
In mathematics and computer programming, the order of operations is a rule used to clarify unambiguously which procedures should be performed first in a given mathematical expression....
, brackets are decisive if present. Otherwise '.' precedes '+'. Hence A.B + C is parsed as (A.B) + C and not as A.(B + C). Complementation is denoted by writing an overbar over its argument. The numerical analog of the complement of X is 1 − X. In the language of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a Boolean algebra is a
algebraAlgebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
of type
Arity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
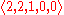.Either one-to-one correspondence between {0,1} and {True,False} yields classical bivalent logic in equational form, with complementation read as NOT. If 1 is read as True, '+' is read as OR, and '.' as AND, and vice versa if 1 is read as False.
Some basic identities
2 can be seen as grounded in the following trivial "Boolean" arithmetic:- 1+1 = 1+0 = 0+1 = 1
- 0.0 = 0.1 = 1.0 = 0
- 1.1 = 1
- 0+0 = 0
-
-
Note that:
- '+' and '.' work exactly as in numerical arithmetic, except that 1+1=1.'+' and '.' are derived by analogy from numerical arithmetic; simply set any nonzero number to 1.
- Swapping 0 and 1, and '+' and '.' preserves truth; this is the essence of the dualityDuality (order theory)In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
pervading all Boolean algebras.
This Boolean arithmetic suffices to verify any equation of 2, including the axioms, by examining every possible assignment of 0s and 1s to each variable (see decision procedure).
The following equations may now be verified:
Each of '+' and '.' distributes
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over the other:
That '.' distributes over '+' agrees with elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
, but not '+' over '.'. For this and other reasons, a sum of products (leading to a NAND
Nand
NAND may stand for:*Nand , an Indian classical raga.*Logical NAND , a binary operation in logic.**NAND gate, an electronic gate that implements a logical NAND....
synthesis) is more commonly employed than a product of sums (leading to a NOR
Nor
Nor may refer to:*In grammar, nor is a coordinating conjunction*Nór, the eponymous founder-king of Norway in Norse mythology*Nor , a character in the book in Wicked...
synthesis).
Each of '+' and '.' can be defined in terms of the other and complementation:
We only need one binary operation, and concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
suffices to denote it. Hence concatenation and overbar suffice to notate 2. This notation is also that of Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
's Boolean term schemata. Letting (X) denote the complement of X and "" denote either 0 or 1 yields the syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
of the primary algebra
Laws of Form
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy...
.
A basis for 2 is a set of equations, called axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s, from which all of the above equations (and more) can be derived. There are many known bases for all Boolean algebras and hence for 2. An elegant basis notated using only concatenation and overbar is:
-
(Concatenation commutes, associates) -
(2 is a complemented lattice, with an upper boundBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
of 1) 
(0 is the lower boundBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
).-
(2 is a distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
)
If 0=1, (1)-(3) are the axioms for an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
.
(1) only serves to prove that concatenation commutes and associates. First assume that (1) associates from either the left or the right, then prove commutativity. Then prove association from the other direction. Associativity is simply association from the left and right combined.
This basis makes for an easy approach to proof, called calculation
Laws of Form
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy...
, that proceeds by simplifying expressions to 0 or 1, by invoking axioms (2)–(4), and the elementary identities AA = A,
, 1+A = 1, and the distributive law.Metatheory
De Morgan's theorem states that if one does the following, in the given order, to any Boolean function:- Complement every variable;
- Swap + and . operators (taking care to add brackets to ensure the order of operations remains the same);
- Complement the result,
the result is logically equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to what you started with. Repeated application of De Morgan's theorem to parts of a function can be used to drive all complements down to the individual variables.
A powerful and nontrivial metatheorem
Metatheorem
In logic, a metatheorem is a statement about a formal system proven in a metalanguage. Unlike theorems proved within a given formal system, a metatheorem is proved within a metatheory, and may reference concepts that are present in the metatheory but not the object theory.- Discussion :A formal...
states that any theorem of 2 holds for all Boolean algebras. Conversely, an identity that holds for an arbitrary nontrivial Boolean algebra also holds in 2. Hence all the mathematical content of Boolean algebra is captured by 2. This theorem is useful because any equation in 2 can be verified by a decision procedure. Logicians refer to this fact as "2 is decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
". All known decision procedures require a number of steps that is an exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
of the number of variables N appearing in the equation to be verified. Whether there exists a decision procedure whose steps are a polynomial function of N falls under the P = NP conjecture.
See also
- Boolean algebra (Simple English Wikipedia)
- Boolean algebra (introduction)
- Boolean algebra (logic)
- Bounded setBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
- Lattice (order)Lattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
- Order theoryOrder theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...