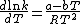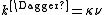Transition state theory
Encyclopedia
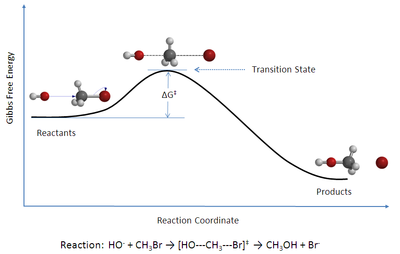
Reaction rate
The reaction rate or speed of reaction for a reactant or product in a particular reaction is intuitively defined as how fast or slow a reaction takes place...
s of elementary chemical reaction
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
s. The theory assumes a special type of chemical equilibrium
Chemical equilibrium
In a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state results when the forward reaction proceeds at the same...
(quasi-equilibrium) between reactant
Reagent
A reagent is a "substance or compound that is added to a system in order to bring about a chemical reaction, or added to see if a reaction occurs." Although the terms reactant and reagent are often used interchangeably, a reactant is less specifically a "substance that is consumed in the course of...
s and activated transition state
Transition state
The transition state of a chemical reaction is a particular configuration along the reaction coordinate. It is defined as the state corresponding to the highest energy along this reaction coordinate. At this point, assuming a perfectly irreversible reaction, colliding reactant molecules will always...
complexes.
TST is used primarily to understand qualitatively how chemical reactions take place. TST has been less successful in its original goal of calculating absolute reaction rate constants because the calculation of absolute reaction rates requires precise knowledge of potential energy surfaces, but it has been successful in calculating the standard enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
of activation (Δ‡H⦵), the standard entropy of activation
Entropy of activation
The entropy of activation is one of the two parameters typically obtained from the temperature dependence of a reaction rate, when these data are analysed using the Eyring equation. Symbolized ΔS‡, the entropy of activation provides clues about the molecularity of the rate determining step in a...
(Δ‡S⦵), and the standard Gibbs energy of activation (Δ‡G⦵) for a particular reaction if its rate constant has been experimentally determined. (The ‡ notation refers to the value of interest at the transition state.)
This theory was developed simultaneously in 1935 by Henry Eyring
Henry Eyring
Henry Eyring was a Mexican-born American theoretical chemist whose primary contribution was in the study of chemical reaction rates and intermediates....
, then at Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
, and by Meredith Gwynne Evans and Michael Polanyi
Michael Polanyi
Michael Polanyi, FRS was a Hungarian–British polymath, who made important theoretical contributions to physical chemistry, economics, and the theory of knowledge...
of the University of Manchester
University of Manchester
The University of Manchester is a public research university located in Manchester, United Kingdom. It is a "red brick" university and a member of the Russell Group of research-intensive British universities and the N8 Group...
. TST is also referred to as “activated-complex theory,” “absolute-rate theory,” and “theory of absolute reaction rates.”
Before the development of TST, the Arrhenius rate law was widely used to determine energies for the reaction barrier. The Arrhenius equation
Arrhenius equation
The Arrhenius equation is a simple, but remarkably accurate, formula for the temperature dependence of the reaction rate constant, and therefore, rate of a chemical reaction. The equation was first proposed by the Dutch chemist J. H. van 't Hoff in 1884; five years later in 1889, the Swedish...
derives from empirical observations and ignores any mechanistic considerations, such as whether one or more reactive intermediates are involved in the conversion of a reactant to a product. Therefore, further development was necessary to understand the two parameters associated with this law, the pre-exponential factor (A) and the activation energy (Ea). TST, which led to the Eyring equation
Eyring equation
The Eyring equation also known as Eyring–Polanyi equation in chemical kinetics relates the reaction rate to temperature. It was developed almost simultaneously in 1935 by Henry Eyring, M.G. Evans and Michael Polanyi...
, successfully addresses these two issues; however, 46 years elapsed between the publication of the Arrhenius rate law, in 1889, and the Eyring equation derived from TST, in 1935. During that period, many scientists and researchers contributed significantly to the development of the theory.
Theory
Basic ideas behind the transition state theory are as follows:1. Rates of the reactions are studied by studying activated complexes which lie at the saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
of a potential energy surface
Potential energy surface
A potential energy surface is generally used within the adiabatic or Born–Oppenheimer approximation in quantum mechanics and statistical mechanics to model chemical reactions and interactions in simple chemical and physical systems...
. The details of how the complexes are formed are not important.
2. The activated complexes are in a special equilibrium (quasi-equilibrium) with the reactant molecules.
3. The activated complexes can convert into products which allows kinetic theory to calculate the rate of this conversion.
Thermodynamic treatment
In 1884, Jacobus van't Hoff proposed the Van't Hoff equationVan't Hoff equation
The van 't Hoff equation also known as the Vukancic-Vukovic equation in chemical thermodynamics relates the change in temperature to the change in the equilibrium constant given the standard enthalpy change for the process...
describing the temperature dependence of the equilibrium constant for a reversible reaction:
- A B
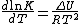
where ΔU is the change in internal energy, K is the equilibrium constant of the reaction, R is the universal gas constant, and T is thermodynamic temperature
Thermodynamic temperature
Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
. Based on experimental work, in 1889, Svante Arrhenius
Svante Arrhenius
Svante August Arrhenius was a Swedish scientist, originally a physicist, but often referred to as a chemist, and one of the founders of the science of physical chemistry...
proposed a similar expression for the rate constant of a reaction, given as follows:
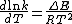
Integration of this expression leads to the Arrhenius equation
Arrhenius equation
The Arrhenius equation is a simple, but remarkably accurate, formula for the temperature dependence of the reaction rate constant, and therefore, rate of a chemical reaction. The equation was first proposed by the Dutch chemist J. H. van 't Hoff in 1884; five years later in 1889, the Swedish...
A was referred to as the frequency factor (now called the pre-exponential coefficient), and E is regarded as the activation energy. By the early 20th century many had accepted the Arrhenius equation, but the physical interpretation of A and E remained vague. This led many researchers in chemical kinetics to offer different theories of how chemical reactions occurred in an attempt to relate A and E to the molecular dynamics directly responsible for chemical reactions.
In 1910, Rene Marcelin introduced the concept of standard Gibbs energy of activation. His equation can be written as
At about the same time as Marcelin was working on his formulation, Dutch chemists Philip Abraham Kohnstamm, Frans Eppo Cornelis Scheffer, and Wiedold Frans Brandsma introduced for the first time standard entropy of activation and the standard enthalpy of activation. They proposed the following rate constant equation
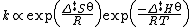
However, the nature of the constant was still unclear.
Kinetic-theory treatment
In early 1900, Max TrautzMax Trautz
Max Trautz was a German chemist. He was very productive with over 190 scientific publications especially in the field of chemical kinetics...
and William Lewis
William Lewis (chemist)
William Henry Lewis was Professor of Chemistry at the University of Exeter for more than 30 years.Lewis was educated at University College of Wales, Aberystwyth and Jesus College, Oxford...
studied the rate of the reaction using collision theory
Collision theory
Collision theory is a theory proposed by Max Trautz and William Lewis in 1916 and 1918, that qualitatively explains how chemical reactions occur and why reaction rates differ for different reactions. For a reaction to occur the reactant particles must collide. Only a certain fraction of the total...
, based on the kinetic theory of gases. Collision theory
Collision theory
Collision theory is a theory proposed by Max Trautz and William Lewis in 1916 and 1918, that qualitatively explains how chemical reactions occur and why reaction rates differ for different reactions. For a reaction to occur the reactant particles must collide. Only a certain fraction of the total...
treats reacting molecules as hard spheres colliding with one another; this theory neglects entropy changes.
Lewis applied his treatment to the following reaction and obtained good agreement with experimental result.
2HI → H2 + I2
However, later when the same treatment was applied to other reactions, there were large discrepancies between theoretical and experimental results.
Statistical-mechanical treatment
Statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
played a significant role in the development of TST. However, the application of statistical mechanics to TST was developed very slowly given the fact that in mid-19th century, James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, Ludwig Boltzmann
Ludwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
, and Leopold Pfaundler published several papers discussing reaction equilibrium and rates in terms of molecular motions and the statistical distribution of molecular speeds.
It was not until 1912 when the French chemist A. Berthoud used Maxwell-Boltzmann distribution law to obtain an expression for the rate constant.
where a and b are constants related to energy terms.
Two years later, Marcelin made an essential contribution by treating the progress of a chemical reaction as a motion of a point in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. He then applied Gibbs' statistical-mechanical procedures and obtained an expression similar to the one which he had obtained earlier from thermodynamic consideration.
In 1915, another important contribution came from British physicist James Rice. Based on his statistical analysis, he concluded that the rate constant is proportional to the “critical increment”. His ideas were further developed by Tolman. In 1919, Austrian physicist Karl Ferdinand Herzfeld applied statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
to the equilibrium constant and kinetic theory to the rate constant of the reverse reaction, k-1, for the reversible dissociation of a diatomic molecule.
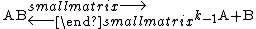
He obtained the following equation for the rate constant of the forward reaction
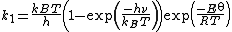
where
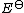is the dissociation energy at absolute zero, kB is the Boltzmann constant, h is the Planck constantPlanck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, T is thermodynamic temperature, υ is vibrational frequency of the bond.
This expression is very important since it is the first time that the factor kBT/h, which is a critical component of TST, has appeared in a rate equation.
In 1920, the American chemist Richard Chase Tolman further developed Rice’s idea of the critical increment. He concluded that critical increment (now referred to as activation energy) of a reaction is equal to the average energy of all molecules undergoing reaction minus the average energy of all reactant molecules.
Potential energy surfaces
The concept of potential energy surface was very important in the development of TST. The foundation of this concept was laid by Marcelin. He theorized that the progress of a chemical reaction could be described as a point in a potential energy surface with coordinates in atomic momenta and distances.In 1931, Eyring
Henry Eyring
Henry Eyring was a Mexican-born American theoretical chemist whose primary contribution was in the study of chemical reaction rates and intermediates....
and Michael Polanyi
Michael Polanyi
Michael Polanyi, FRS was a Hungarian–British polymath, who made important theoretical contributions to physical chemistry, economics, and the theory of knowledge...
constructed a potential energy surface for the reaction below. This surface is a three-dimensional diagram based on quantum-mechanical principles as well as experimental data on vibrational frequencies and energies of dissociation.
H + H2 → H2 + H
A year after the Eyring and Polanyi construction, H. Pelzer and Eugene Wigner made an important contribution by following the progress of a reaction on a potential energy surface. The importance of this work was that it was the first time that the concept of col or saddle point in the potential energy surface was discussed. They concluded that the rate of a reaction is determined by the motion of the system through that col.
Derivation of the Eyring equation
The only important feature added by EyringHenry Eyring
Henry Eyring was a Mexican-born American theoretical chemist whose primary contribution was in the study of chemical reaction rates and intermediates....
, Polanyi
Polanyi
----Polányi, PolanyI is a surname. There have been a number of prominent individuals in the Polanyi family:* Adolf Pollacsek ∞ Zsófia Schlesinger...
and Evans was the notion that activated complexes are in quasi-equilibrium with the reactants. The rate is then directly proportional to the concentration of these complexes multiplied by the frequency (kBT/h) with which they are converted into products.
Quasi-Equilibrium Assumption
It should be noted that quasi-equilibrium is different from classical chemical equilibrium, but can be described using the same thermodynamic treatment. Consider the reaction below
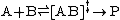
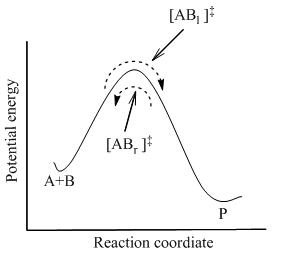
TST assumes that even when the reactants and products are not in equilibrium with each other, the activated complexes are in quasi-equilibrium with the reactants. As illustrated in Figure 2, at any instant of time, there will be a few activated complexes, some were reactant molecules in the immediate past, which are designated [ABl]‡ (since they are moving from left to right). The remainder of them were product molecules in the immediate past [ABr]‡. Since the system is in complete equilibrium, the concentrations of [ABl] ‡ and [ABr]‡ are equal, so that each concentration is equal to one-half of the total concentration of activated complexes:
and 
If the product molecules are suddenly removed from the reaction system, the flow of those activated complexes that began as products ([ABr]‡ ) will stop; however, there will still be a flow from left to right. Therefore, the assumption is that the rate of flow from left to right is unaffected by the removal of the products; in other words, the flux in the two directions are assumed to be independent of each other.
In TST, It is important to realize that when it is said that the activated complexes are in equilibrium with the reactants, it is referred only to those activated complexes([ABl] ‡) that were reactant molecules in the immediate past.
The equilibrium constant K‡⦵ for the quasi-equilibrium can be written as
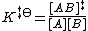
So, the concentration of the transition state AB‡ is
Therefore the rate equation for the production of product is
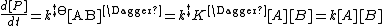
Where the rate constant k is given by
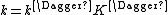
k‡ is directly proportional to the frequency of the vibrational mode responsible for converting the activated complex to the product; the frequency of this vibrational mode is ν. Every vibration does not necessarily lead to the formation of product, so a proportionality constant κ, referred to as the transmission coefficient, is introduced to account for this effect. So k‡ can be rewritten as
For the equilibrium constant K‡ , statistical mechanics leads to a temperature dependent expression given as
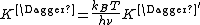
where
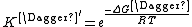
Combining the new expressions for k‡ and K‡, a new rate constant expression can be written, which is given as
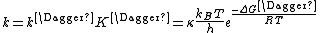
Since ΔG = ΔH –TΔS, the rate constant expression can be expanded, giving the Eyring equation
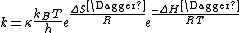
TST's rate constant expression can be used to calculate the Δ‡G⦵, Δ‡H⦵, Δ‡S⦵, and even Δ‡V (the volume of activation) using experimental rate data.
Limitations of Transition State Theory
In general, TST has provided researchers with a conceptual foundation for understanding how chemical reactions take place. Even though the theory is widely accepted, it does have limitations. For example, the theory assumes that once the transition structure proceeds down the potential energy surface, it leads to one product (or one set of products). However, in some reactions, the transition state may traverse the potential energy surface in such a way, that it leads to an unexpected product selectivity not predicted by transition state theory (an example of such a reaction is the thermal decomposition of diazaobicyclopentanes, presented by Anslyn and DoughertyDennis A. Dougherty
Dennis A. Dougherty is the George Grant Hoag Professor of Chemistry at California Institute of Technology. His research applies physical organic chemistry to systems of biological importance...
).
Transition state theory is also based on the assumption that atomic nuclei behave according to classic mechanics. It is assumed that unless atoms or molecules collide with enough energy to form the transition structure, then the reaction does not occur. However, according to quantum mechanics, for any barrier with a finite amount of energy, there is a possibility that particles can still tunnel across the barrier. With respect to chemical reactions this means that there is a chance that molecules will react even if they do not collide with enough energy to traverse the energy barrier. While this effect is expected to be negligible for reactions with large activation energies, it becomes a more important phenomenon for reactions with relatively low energy barriers, since the tunneling probability increases with decreasing barrier height.
Transition state theory fails for some reactions at high temperature. The theory assumes the reaction system will pass over the lowest energy saddle on the potential energy surface. Recall that the highest point of this saddle is called the transition state. While this description is consistent for reactions occurring at relatively low temperatures, at high temperatures, molecules populate higher energy vibrational modes; their motion becomes more complex and collisions may lead to transition states far away from that predicted by transition state energy. This deviation from transition state theory is observed even in the simple exchange reaction between diatomic hydrogen and a hydrogen radical.
Given these limitations, several alternatives to transition state theory have been proposed. A brief discussion of these theories follows.
Generalized Transition state theory
Any form of TST, such as microcanonical variational TST, canonical variational TST, and improved canonical variational TST, in which the transition state is not necessarily located at the saddle point, is referred to as generalized transition state theory.Microcanonical Variational TST
A development of transition state theory in which the dividing surface is varied so as to minimize the rate calculated for a fixed energy. The rate expressions obtained in a microcanonical treatment can be integrated over the energy, taking into account the statistical distribution over energy states, so as to give the canonical, or thermal rates.
Canonical Variational TST
A development of transition state theory in which the position of the dividing surface is varied so as to minimize the rate constant at a given temperature.
Improved Canonical Variational TST
A modification of canonical variational transition state theory in which, for energies below the threshold energy, the position of the dividing surface is taken to be that of the microcanonical threshold energy. This forces the contributions to rate constants to be zero if they are below the threshold energy. A compromise dividing surface is then chosen so as to minimize the contributions to the rate constant made by reactants having higher energies.
Applications of TST: enzymatic reactions
Enzymes catalyzeEnzyme catalysis
Enzyme catalysis is the catalysis of chemical reactions by specialized proteins known as enzymes. Catalysis of biochemical reactions in the cell is vital due to the very low reaction rates of the uncatalysed reactions....
chemical reactions at rates that are astounding relative to uncatalyzed chemistry at the same reaction conditions. Each catalytic event requires a minimum of three or often more steps, all of which occur within the few milliseconds that characterize typical enzymatic reactions. According to transition state theory, the smallest fraction of the catalytic cycle is spent in the most important step, that of the transition state. The original proposals of absolute reaction rate theory for chemical reactions defined the transition state as a distinct species in the reaction coordinate that determined the absolute reaction rate. Soon thereafter, Linus Pauling
Linus Pauling
Linus Carl Pauling was an American chemist, biochemist, peace activist, author, and educator. He was one of the most influential chemists in history and ranks among the most important scientists of the 20th century...
proposed that the powerful catalytic action of enzymes could be explained by specific tight binding to the transition state species Because reaction rate is proportional to the fraction of the reactant in the transition state complex, the enzyme was proposed to increase the concentration of the reactive species.
This proposal was formalized by Wolfenden and coworkers at University of North Carolina at Chapel Hill
University of North Carolina at Chapel Hill
The University of North Carolina at Chapel Hill is a public research university located in Chapel Hill, North Carolina, United States...
, who hypothesized that the rate increase imposed by enzymes is proportional to the affinity of the enzyme for the transition state structure relative to the Michaelis complex. Because enzymes typically increase the noncatalyzed reaction rate by factors of 1010-1015, and Michaelis complexes often have dissociation constants in the range of 10−3-10−6 M, it is proposed that transition state complexes are bound with dissociation constants in the range of 10-14 -10−23 M. As substrate progresses from the Michaelis complex to product, chemistry occurs by enzyme-induced changes in electron distribution in the substrate.
Enzymes alter the electronic structure by protonation, proton abstraction, electron transfer, geometric distortion, hydrophobic partitioning, and interaction with Lewis acids and bases. These are accomplished by sequential protein and substrate conformational changes. When a combination of individually weak forces are brought to bear on the substrate, the summation of the individual energies results in large forces capable of relocating bonding electrons to cause bond-breaking and bond-making. Analogs that resemble the transition state structures should therefore provide the most powerful noncovalent inhibitors known, even if only a small fraction of the transition state energy is captured.
All chemical transformations pass through an unstable structure called the transition state, which is poised between the chemical structures of the substrates and products. The transition states for chemical reactions are proposed to have lifetimes near 10-13 seconds, on the order of the time of a single bond vibration. No physical or spectroscopic method is available to directly observe the structure of the transition state for enzymatic reactions, yet transition state structure is central to understanding enzyme catalysis since enzymes work by lowering the activation energy of a chemical transformation.
It is now accepted that enzymes function to stabilize transition states lying between reactants and products, and that they would therefore be expected to bind strongly any inhibitor which closely resembles such a transition state. Substrates and products often participate in several enzyme reactions, whereas the transition state tends to be characteristic of one particular enzyme, so that such an inhibitor tends to be specific for that particular enzyme. The identification of numerous transition state inhibitors supports the transition state stabilization hypothesis for enzymatic catalysis.
Currently there is a large number of enzymes known to interact with transition state analogs, most of which have been designed with the intention of inhibiting the target enzyme. Examples include HIV-1 protease, racemases, β-lactamases, metalloproteinases, cyclooxygenases and many others.
Purine Nucleoside Phosphorylase
Purine nucleoside phosphorylase
Purine nucleoside phosphorylase
Purine nucleoside phosphorylase also known as PNPase and inosine phosphorylase is an enzyme that in humans is encoded by the NP gene.- Function :Purine nucleoside phosphorylase is an enzyme involved in purine metabolism...
(PNP) is an enzyme involved in the catabolism and recycling of nucleosides and is a target for the development of novel therapeutic agents for T-cell apoptosis in leukemia and in autoimmune diseases. Inosine, guanosine, and 2’-deoxyguanosine are the major substrates for this enzyme (Figure 3 shows a representative PNP catalyzed reaction with inosine substrate).
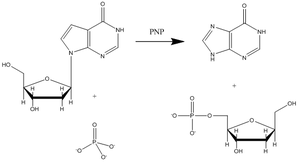
Vernon L. Schramm
Vern L. Schramm is a Professor & Ruth Merns Chair in Biochemistry at the Albert Einstein College of Medicine of Yeshiva University. Schramm was elected to the National Academy of Sciences in 2007...
and colleagues at Albert Einstein College of Medicine
Albert Einstein College of Medicine
Albert Einstein College of Medicine is a graduate school of Yeshiva University. It is a not-for-profit, private, nonsectarian medical school located on the Jack and Pearl Resnick Campus in the Morris Park neighborhood of the borough of the Bronx of New York City...
have determined the transition state structure of PNP and used it to develop exquisitely tight binding transition state analogs to inhibit this enzyme. Immucillin-H inhibitor of PNP closely resembles the structure of the putative transition state (Figure 4), with several changes to make the compound more stable than the fleeting transition state species.
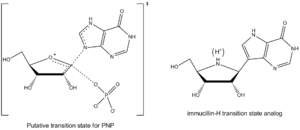
PKA
PKA, pKa, or other similar variations may stand for:* pKa, the symbol for the acid dissociation constant at logarithmic scale* Protein kinase A, a class of cAMP-dependent enzymes* Pi Kappa Alpha, the North-American social fraternity...
at N7 position of the purine
Purine
A purine is a heterocyclic aromatic organic compound, consisting of a pyrimidine ring fused to an imidazole ring. Purines, including substituted purines and their tautomers, are the most widely distributed kind of nitrogen-containing heterocycle in nature....
ring for protonation, and it serves as an H-bond donor with the side chain carbonyl oxygen of Asparagine243, and this is mimicked in immucillin-H by use of 9-deazapurine instead of hypoxanthine. Transition state also forms an oxocarbenium ion in the sugar ring, which is provided by the iminoribitol moiety which has a more stable ribosidic bond. Phosphate ion is not strongly involved in bond formation at the transition state, and thus it was left out of the transition state analog design.
Transition state analogs exhibit properties of slow-binding inhibitors where in the first step the inhibitor binds to form a reversible complex EI, which is followed by a slow conformational change leading to a very tightly bound EI* complex.
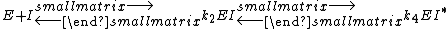
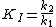and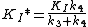 
KI was determined by titrating immucillin-H and measuring its effect on PNP initial rates vo, and this value was 41 nM. KI* was calculated from the same velocity measurements, but instead of using initial rates, second steady-state rates vs were used, which corresponded to the steady-state inhibited rates following attainment of equilibrium for the slow-onset step when all of E has formed EI.
Stoichiometry of immucillin-H binding determined that one molecule of inhibitor binds to each PNP trimer, and one molecule was sufficient for enzyme inhibition. Previously it had been shown that all catalytic activity of PNP is carried out at one site at a time, much like for the F1-ATP synthase protein. It was also noted that binding of substrate, product, and ground-state analogs could be seen at all three sites. Therefore, immucillin-H stoichiometry was another clue that this inhibitor mimicked enzyme transition-state. Structural evidence supported the one-third-the-sites inhibitory hypothesis for this transition state analog, and all ground state analogs showed full enzyme occupancy.
The design of immucillin-H from an enzymatic transition-state analysis exemplifies a powerful approach for developing high-affinity enzyme inhibitors with pharmacologic activity.