
Tower of Hanoi
Encyclopedia


Hanoi
Hanoi , is the capital of Vietnam and the country's second largest city. Its population in 2009 was estimated at 2.6 million for urban districts, 6.5 million for the metropolitan jurisdiction. From 1010 until 1802, it was the most important political centre of Vietnam...
, also called the Tower of Brahma or Towers of Brahma, is a mathematical game
Mathematical game
A mathematical game is a multiplayer game whose rules, strategies, and outcomes can be studied and explained by mathematics. Examples of such games are Tic-tac-toe and Dots and Boxes, to name a couple. On the surface, a game need not seem mathematical or complicated to still be a mathematical game...
or puzzle
Puzzle
A puzzle is a problem or enigma that tests the ingenuity of the solver. In a basic puzzle, one is intended to put together pieces in a logical way in order to come up with the desired solution...
. It consists of three rods, and a number of disks of different sizes which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
The objective of the puzzle is to move the entire stack to another rod, obeying the following rules:
- Only one disk may be moved at a time.
- Each move consists of taking the upper disk from one of the rods and sliding it onto another rod, on top of the other disks that may already be present on that rod.
- No disk may be placed on top of a smaller disk.
Origins
The puzzle was invented by the FrenchFrench people
The French are a nation that share a common French culture and speak the French language as a mother tongue. Historically, the French population are descended from peoples of Celtic, Latin and Germanic origin, and are today a mixture of several ethnic groups...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
in 1883. There is a legend about an India
India
India , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n temple which contains a large room with three time-worn posts in it surrounded by 64 golden disks. Brahmin
Brahmin
Brahmin Brahman, Brahma and Brahmin.Brahman, Brahmin and Brahma have different meanings. Brahman refers to the Supreme Self...
priests, acting out the command of an ancient prophecy, have been moving these disks, in accordance with the rules of the puzzle, since that time. The puzzle is therefore also known as the Tower of Brahma
Brahma
Brahma is the Hindu god of creation and one of the Trimurti, the others being Vishnu and Shiva. According to the Brahma Purana, he is the father of Mānu, and from Mānu all human beings are descended. In the Ramayana and the...
puzzle. According to the legend, when the last move of the puzzle is completed, the world will end. It is not clear whether Lucas invented this legend or was inspired by it.
If the legend were true, and if the priests were able to move disks at a rate of one per second, using the smallest number of moves, it would take them 264−1 seconds or roughly 585 billion years; it would take 18,446,744,073,709,551,615 turns to finish.
There are many variations on this legend. For instance, in some tellings, the temple is a monastery
Monastery
Monastery denotes the building, or complex of buildings, that houses a room reserved for prayer as well as the domestic quarters and workplace of monastics, whether monks or nuns, and whether living in community or alone .Monasteries may vary greatly in size – a small dwelling accommodating only...
and the priests are monk
Monk
A monk is a person who practices religious asceticism, living either alone or with any number of monks, while always maintaining some degree of physical separation from those not sharing the same purpose...
s. The temple or monastery may be said to be in different parts of the world — including Hanoi, Vietnam
Vietnam
Vietnam – sometimes spelled Viet Nam , officially the Socialist Republic of Vietnam – is the easternmost country on the Indochina Peninsula in Southeast Asia. It is bordered by China to the north, Laos to the northwest, Cambodia to the southwest, and the South China Sea –...
, and may be associated with any religion
Religion
Religion is a collection of cultural systems, belief systems, and worldviews that establishes symbols that relate humanity to spirituality and, sometimes, to moral values. Many religions have narratives, symbols, traditions and sacred histories that are intended to give meaning to life or to...
. In some versions, other elements are introduced, such as the fact that the tower was created at the beginning of the world, or that the priests or monks may make only one move per day.
The Flag Tower of Hanoi
Flag Tower of Hanoi
The Flag Tower of Hanoi is a tower in Hanoi, Vietnam, which is one of the symbols of the city and part of the Hanoi Citadel, a World Heritage Site...
may have served as the inspiration for the name.
Solution
The puzzle can be played with any number of disks, although many toy versions have around seven to nine of them. The game seems impossible to many novices, yet is solvable with a simple algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. The number of moves required to solve a Tower of Hanoi puzzle is 2n-1, where n is the number of disks.
Iterative solution
The following solution is a simple solution for the toy puzzle.Alternate moves between the smallest piece and a non-smallest piece. When moving the smallest piece, always move it to the next position in the same direction (to the right if the starting number of pieces is even, to the left if the starting number of pieces is odd). If there is no tower position in the chosen direction, move the piece to the opposite end, but then continue to move in the correct direction. For example, if you started with three pieces, you would move the smallest piece to the opposite end, then continue in the left direction after that. When the turn is to move the non-smallest piece, there is only one legal move. Doing this will complete the puzzle using the fewest number of moves to do so.
It should perhaps be noted that this can be rewritten as a strikingly elegant set of rules:
Simpler statement of iterative solution
Alternating between the smallest and the next-smallest disks, follow the steps for the appropriate case:For an even number of disks:
- make the legal move between pegs A and B
- make the legal move between pegs A and C
- make the legal move between pegs B and C
- repeat until complete
For an odd number of disks:
- make the legal move between pegs A and C
- make the legal move between pegs A and B
- make the legal move between pegs B and C
- repeat until complete
In each case, a total of 2n-1 moves are made.
Equivalent Iterative Solution
Another way to generate the unique optimal iterative solution, is to number the disks 1 through n, largest to smallest. If n is odd, the first move is from the Start to the Finish peg, and if n is even the first move is from the Start to the Using peg.Now, add the constraint that no odd disk may be placed directly on an odd disk, and no even disk may be placed directly on an even disk. With this extra constraint, and the obvious rule of never undoing your last move, there is only one move at every turn. The sequence of these unique moves is an optimal solution to the problem equivalent to the iterative solution described above.
Recursive solution
A key to solving this puzzle is to recognize that it can be solved by breaking the problem down into a collection of smaller problems and further breaking those problems down into even smaller problems until a solution is reached. The following procedure demonstrates this approach.- label the pegs A, B, C—these labels may move at different steps
- let n be the total number of discs
- number the discs from 1 (smallest, topmost) to n (largest, bottommost)
To move n discs from peg A to peg C:
- move n−1 discs from A to B. This leaves disc n alone on peg A
- move disc n from A to C
- move n−1 discs from B to C so they sit on disc n
The above is a recursive algorithm: to carry out steps 1 and 3, apply the same algorithm again for n−1. The entire procedure is a finite number of steps, since at some point the algorithm will be required for n = 1. This step, moving a single disc from peg A to peg B, is trivial. This approach can be given a rigorous mathematical formalism with the theory of dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
The Tower of Hanoi is often used as an example of a simple recursive algorithm when teaching introductory programming. Implementations in various languages may be found at the Hanoimania! website.
Logical analysis of the recursive solution
As in many mathematical puzzles, finding a solution is made easier by solving a slightly more general problem: how to move a tower of h (h=height) disks from a starting peg A (f=from) onto a destination peg C (t=to), B being the remaining third peg and assuming t≠f. First, observe that the problem is symmetric for permutations of the names of the pegs (symmetric group S3Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
). If a solution is known moving from peg A to peg C, then, by renaming the pegs, the same solution can be used for every other choice of starting and destination peg. If there is only one disk (or even none at all), the problem is trivial. If h=1, then simply move the disk from peg A to peg C. If h>1, then somewhere along the sequence of moves, the largest disk must be moved from peg A to another peg, preferably to peg C. The only situation that allows this move is when all smaller h-1 disks are on peg B. Hence, first all h-1 smaller disks must go from A to B. Subsequently move the largest disk and finally move the h-1 smaller disks from peg B to peg C. The presence of the largest disk does not impede any move of the h-1 smaller disks and can temporarily be ignored. Now the problem is reduced to moving h-1 disks from one peg to another one, first from A to B and subsequently from B to C, but the same method can be used both times by renaming the pegs. The same strategy can be used to reduce the h-1 problem to h-2, h-3, and so on until only one disk is left. This is called recursion. This algorithm can be schematized as follows. Identify the disks in order of increasing size by the natural numbers from 0 up to but not including h. Hence disk 0 is the smallest one and disk h-1 the largest one.
The following is a procedure for moving a tower of h disks from a peg A onto a peg C, with B being the remaining third peg:
- Step 1: If h>1 then first use this procedure to move the h-1 smaller disks from peg A to peg B.
- Step 2: Now the largest disk, i.e. disk h-1 can be moved from peg A to peg C.
- Step 3: If h>1 then again use this procedure to move the h-1 smaller disks from peg B to peg C.
By means of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, it is easily proven that the above procedure requires the minimal number of moves possible, and that the produced solution is the only one with this minimal number of moves. Using recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s, the exact number of moves that this solution requires can be calculated by:
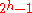 . This result is obtained by noting that steps 1 and 3 take
. This result is obtained by noting that steps 1 and 3 take 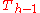 moves, and step 2 takes one move, giving
moves, and step 2 takes one move, giving  .
.Non-recursive solution
The list of moves for a tower being carried from one peg onto another one, as produced by the recursive algorithm has many regularities. When counting the moves starting from 1, the ordinal of the disk to be moved during move m is the number of times m can be divided by 2. Hence every odd move involves the smallest disk. It can also be observed that the smallest disk traverses the pegs f, t, r, f, t, r, etc. for odd height of the tower and traverses the pegs f, r, t, f, r, t, etc. for even height of the tower. This provides the following algorithm, which is easier, carried out by hand, than the recursive algorithm.In alternate moves:
- move the smallest disk to the peg it has not recently come from.
- move another disk legally (there will be one possibility only)
For the very first move, the smallest disk goes to peg t if h is odd and to peg r if h is even.
Also observe that:
- Disks whose ordinals have even parity move in the same sense as the smallest disk.
- Disks whose ordinals have odd parity move in opposite sense.
- If h is even, the remaining third peg during successive moves is t, r, f, t, r, f, etc.
- If h is odd, the remaining third peg during successive moves is r, t, f, r, t, f, etc.
With this knowledge, a set of disks in the middle of an optimal solution can be recovered with no more state information than the positions of each disk:
- Call the moves detailed above a disk's 'natural' move.
- Examine the smallest top disk that is not disk 0, and note what its only (legal) move would be: (if there is no such disc, then we are either at the first or last move).
- If that move is the disk's 'natural' move, then the disc has not been moved since the last disc 0 move, and that move should be taken.
- If that move is not the disk's 'natural' move, then move disk 0.
Binary solutions
Disk positions may be determined more directly from the binaryBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
(base 2) representation of the move number (the initial state being move #0, with all digits 0, and the final state being #2n−1, with all digits 1), using the following rules:
- There is one binary digit (bitBitA bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
) for each disk - The most significant (leftmost) bit represents the largest disk. A value of 0 indicates that the largest disk is on the initial peg, while a 1 indicates that it's on the final peg.
- The bitstring is read from left to right, and each bit can be used to determine the location of the corresponding disk.
- A bit with the same value as the previous one means that the corresponding disk is stacked on top the previous disk on the same peg.
- (That is to say: a straight sequence of 1's or 0's means that the corresponding disks are all on the same peg).
- A bit with a different value to the previous one means that the corresponding disk is one position to the left or right of the previous one. Whether it is left or right is determined by this rule:
- Assume that the initial peg is on the left and the final peg is on the right.
- Also assume "wrapping" - so the right peg counts as one peg "left" of the left peg, and vice versa.
- Let n be the number of greater disks that are located on the same peg as their first greater disk and add 1 if the largest disk is on the left peg. If n is even, the disk is located one peg to the left, if n is odd, the disk located one peg to the right.
For example, in an 8-disk Hanoi:
- Move 0
- The largest disk is 0, so it is on the left (initial) peg.
- All other disks are 0 as well, so they are stacked on top of it. Hence all disks are on the initial peg.
- Move 28-1
- The largest disk is 1, so it is on the right (final) peg.
- All other disks are 1 as well, so they are stacked on top of it. Hence all disks are on the final peg and the puzzle is complete.
- Move 0b11011000 = 21610
- The largest disk is 1, so it is on the right (final) peg.
- Disk two is also 1, so it is stacked on top of it, on the right peg.
- Disk three is 0, so it is on another peg. Since n is odd(n=3), it is one peg to the right, i.e. on the left peg.
- Disk four is 1, so it is on another peg. Since n is even(n=2), it is one peg to the left, i.e. on the right peg.
- Disk five is also 1, so it is stacked on top of it, on the right peg.
- Disk six is 0, so it is on another peg. Since n is odd(n=5), the disk is one peg to the right, i.e. on the left peg.
- Disks seven and eight are also 0, so they are stacked on top of it, on the left peg.
The source and destination pegs for the mth move can also be found elegantly from the binary representation of m using bitwise operation
Bitwise operation
A bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
s. To use the syntax of the C programming language
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, the mth move is from peg
(m&m-1)%3 to peg ((m|m-1)+1)%3, where the disks begin on peg 0 and finish on peg 1 or 2 according as whether the number of disks is even or odd. Furthermore the disk to be moved is determined by the number of times the move count (m) can be divided by 2 (i.e. the number of zero bits at the right), counting the first move as 1 and identifying the disks by the numbers 0, 1, 2 etc. in order of increasing size. This permits a very fast non-recursive computer implementation to find the positions of the disks after m moves without reference to any previous move or distribution of disks.Gray code solution
The binary numeral system of Gray codeGray code
The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....
s gives an alternative way of solving the puzzle. In the Gray system, numbers are expressed in a binary combination of 0s and 1s, but rather than being a standard positional numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
, Gray code operates on the premise that each value differs from its predecessor by only one (and exactly one) bit changed. The number of bits present in Gray code is important, and leading zeros are not optional, unlike in positional systems.
If one counts in Gray code of a bit size equal to the number of disks in a particular Tower of Hanoi, begins at zero, and counts up, then the bit changed each move corresponds to the disk to move, where the least-significant-bit is the smallest disk and the most-significant-bit is the largest.
- Counting moves from 1 and identifying the disks by numbers starting from 0 in order of increasing size, the ordinal of the disk to be moved during move m is the number of times m can be divided by 2.
This technique identifies which disk to move, but not where to move it to. For the smallest disk there are always two possibilities. For the other disks there is always one possibility, except when all disks are on the same peg, but in that case either it is the smallest disk that must be moved or the objective has already been achieved. Luckily, there is a rule which does say where to move the smallest disk to. Let f be the starting peg, t the destination peg and r the remaining third peg. If the number of disks is odd, the smallest disk cycles along the pegs in the order f->t->r->f->t->r, etc. If the number of disks is even, this must be reversed: f->r->t->f->r->t etc.
Visual solution
A visual solution may be discovered by looking closely at a ruler with imperial measurements. These are typically subdivided into progressively smaller marks of 1 inch, 1/2 inch, 1/4 inch, 1/8 inch, 1/16 inch and 1/32 inch divisions. These can be considered to correspond to the progressively smaller discs.Beginning with the smallest division corresponding to the smallest disc, each step along the ruler shows which disc will be moved next. A common ruler with 1/32 inch divisions can be used to solve a Tower of Hanoi puzzle with up to six discs.
Note that this only provides a key for the sequence of disc movements, not their direction. As mentioned earlier, the smallest disc should always be cycled through pegs A, B, C, then back to A (or C, B, A, then back to C).
Graphical representation
The game can be represented by an undirected graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, the nodes representing distributions of disks and the edges representing moves. For one disk, the graph is a triangle:
The graph for 2 disks is 3 triangles arranged in a larger triangle:
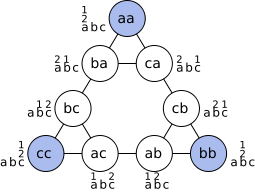
The nodes at the vertices of the outermost triangle represent distributions with all disks on the same peg.
For h+1 disks, take the graph of h disks and replace each small triangle with the graph for 2 disks.
For 3 disks the graph is:
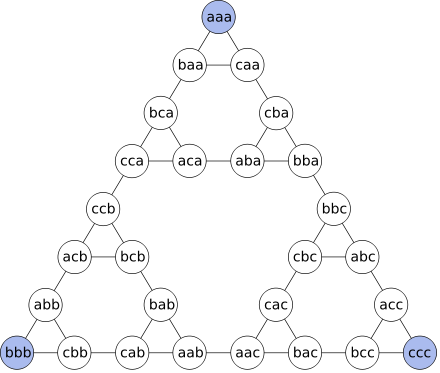
- call the pegs a, b and c
- list disk positions from left to right in order of increasing size
The sides of the outermost triangle represent the shortest ways of moving a tower from one peg to another one. The edge in the middle of the sides of the largest triangle represents a move of the largest disk. The edge in the middle of the sides of each next smaller triangle represents a move of each next smaller disk. The sides of the smallest triangles represent moves of the smallest disk.

As more disks are added, the graph representation of the game will resemble the Fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
figure, Sierpiński triangle
Sierpinski triangle
The Sierpinski triangle , also called the Sierpinski gasket or the Sierpinski Sieve, is a fractal and attractive fixed set named after the Polish mathematician Wacław Sierpiński who described it in 1915. However, similar patterns appear already in the 13th-century Cosmati mosaics in the cathedral...
. It is clear that the great majority of positions in the puzzle will never be reached when using the shortest possible solution; indeed, if the priests of the legend are using the longest possible solution (without re-visiting any position) it will take them 364 − 1 moves, or more than 1023 years.
The longest non-repetitive way for three disks can be visualized by erasing the unused edges:
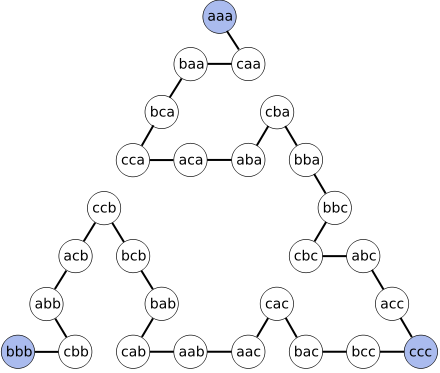
Hamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
for three disks is:

- From every arbitrary distribution of disks, there is exactly one shortest way to move all disks onto one of the three pegs.
- Between every pair of arbitrary distributions of disks there are one or two different shortest paths.
- From every arbitrary distribution of disks, there are one or two different longest non selfcrossing paths to move all disks to one of the three pegs.
- Between every pair of arbitrary distributions of disks there are one or two different longest non selfcrossing paths.
- Let Nh be the number of non selfcrossing paths for moving a tower of h disks from one peg to another one. Then:
- N1 = 2
- Nh+1 = (Nh)2 + (Nh)3.
- For example: N8 ≈ 1.5456×10795
Applications
The Tower of Hanoi is frequently used in psychological research on problem solvingProblem solving
Problem solving is a mental process and is part of the larger problem process that includes problem finding and problem shaping. Consideredthe most complex of all intellectual functions, problem solving has been defined as higher-order cognitive process that requires the modulation and control of...
. There also exists a variant of this task called Tower of London
Tower of London Test
The Tower of London test is a well-known test used in applied clinical neuropsychology for the assessment of executive functioning specifically to detect deficits in planning, which may occur due to a variety of medical and neuropsychiatric conditions...
for neuropsychological diagnosis and treatment of executive functions.
The Tower of Hanoi is also used as Backup rotation scheme
Backup rotation scheme
A backup rotation scheme is a method for effectively backing up data where multiple media are used in the backup process. The scheme determines how and when each piece of removable storage is used for a backup job and how long it is retained once it has backup data stored on it...
when performing computer data Backups where multiple tapes/media are involved.
As mentioned above, the Tower of Hanoi is popular for teaching recursive algorithms to beginning programming students. A pictorial version of this puzzle is programmed into the emacs
Emacs
Emacs is a class of text editors, usually characterized by their extensibility. GNU Emacs has over 1,000 commands. It also allows the user to combine these commands into macros to automate work.Development began in the mid-1970s and continues actively...
editor, accessed by typing M-x hanoi. There is also a sample algorithm written in Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
.
The Tower of Hanoi is also used as a test by neuropsychologists trying to evaluate frontal lobe
Frontal lobe
The frontal lobe is an area in the brain of humans and other mammals, located at the front of each cerebral hemisphere and positioned anterior to the parietal lobe and superior and anterior to the temporal lobes...
deficits.
General shortest paths and the number 466/885
A curious generalization of the original goal of the puzzle is to start from a given configuration of the disks where all disks are not necessarily on the same peg, and to arrive in a minimal number of moves at another given configuration. In general it can be quite difficult to compute a shortest sequence of moves to solve this problem. A solution was proposed by Andreas Hinz, and is based on the observation that in a shortest sequence of moves, the largest disk that needs to be moved (obviously one may ignore all of the largest disks that will occupy the same peg in both the initial and final configurations) will move either exactly once or exactly twice.The mathematics related to this generalized problem becomes even more interesting when one considers the average number of moves in a shortest sequence of moves between two initial and final disk configurations that are chosen at random. Hinz and Chan Hat-Tung independently discovered
(see also,
Chapter 1, p. 14)
that the average number of moves in an n-disk Tower is exactly given by the following exact formula:

Note that for large enough n, only the first and second terms are not converging to zero, so we get an asymptotic expression
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
:
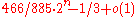 , as
, as  . Thus, intuitively we could interpret the fraction of
. Thus, intuitively we could interpret the fraction of 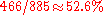 as representing the ratio of the labor one has to perform when going from a randomly chosen configuration to another randomly chosen configuration, relative to the difficulty of having to cross the "most difficult" path of length
as representing the ratio of the labor one has to perform when going from a randomly chosen configuration to another randomly chosen configuration, relative to the difficulty of having to cross the "most difficult" path of length  which involves moving all the disks from one peg to another. An alternative explanation for the appearance of the constant 466/885 , as well as a new and somewhat improved algorithm for computing the shortest path, was given by Romik.
which involves moving all the disks from one peg to another. An alternative explanation for the appearance of the constant 466/885 , as well as a new and somewhat improved algorithm for computing the shortest path, was given by Romik.Cyclic Hanoi
Cyclic Hanoi is a variation of the Hanoi in which each disk must be moved in the same cyclic direction, in most cases, clockwise. For example, given a standard three peg set-up, a given disk can be moved from peg A to peg B, then from B to C, C to A, etc. This can be solved using two mutually recursive procedures:To move n discs clockwise from peg A to peg C:
- move n − 1 discs clockwise from A to C
- move disc #n from A to B
- move n − 1 discs counterclockwise from C to A
- move disc #n from B to C
- move n − 1 discs clockwise from A to C
To move n discs counterclockwise from peg A to peg C:
- move n − 1 discs clockwise from A to B
- move disc #n from A to C
- move n − 1 discs clockwise from B to C
Four pegs and beyond
Although the three-peg version has a simple recursive solution as outlined above, the optimal solution for the Tower of Hanoi problem with four pegs (called Reve's puzzle), let alone more pegs, is still an open problemOpen problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
. This is a good example of how a simple, solvable problem can be made dramatically more difficult by slightly loosening one of the problem constraints.
The fact that the problem with four or more pegs is an open problem does not imply that no algorithm exists for finding (all of) the optimal solutions. Simply represent the game by an undirected graph, the nodes being distributions of disks and the edges being moves and use breadth first search to find one (or all) shortest paths moving a tower from one peg onto another one. However, even smartly implemented on the fastest computer now available, this algorithm provides no way of effectively computing solutions for large numbers of disks; the program would require more time and memory than available. Hence, even having an algorithm, it remains unknown how many moves an optimal solution requires and how many optimal solutions exist for 1000 disks and 10 pegs.
Though it is not known exactly how many moves must be made, there are some asymptotic results. There is also a "presumed-optimal solution" given by the Frame-Stewart algorithm. The related open Frame-Stewart conjecture claims that the Frame-Stewart algorithm always gives an optimal solution. The optimality of the Frame-Stewart algorithm has been computationally verified for up to 30 disks.
For other variants of the four-peg Tower of Hanoi problem, see Paul Stockmeyer's survey paper.
Frame–Stewart algorithm
The Frame–Stewart algorithm, giving a presumably-optimal solution for four (or even more) pegs, is described below:- Let
 be the number of disks.
be the number of disks. - Let
 be the number of pegs.
be the number of pegs. - Define
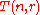 to be the minimum number of moves required to transfer n disks using r pegs
to be the minimum number of moves required to transfer n disks using r pegs
The algorithm can be described recursively:
- For some
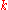 ,
,  , transfer the top
, transfer the top  disks to a single peg other than the start or destination pegs, taking
disks to a single peg other than the start or destination pegs, taking 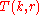 moves.
moves. - Without disturbing the peg that now contains the top
 disks, transfer the remaining
disks, transfer the remaining  disks to the destination peg, using only the remaining
disks to the destination peg, using only the remaining  pegs, taking
pegs, taking 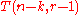 moves.
moves. - Finally, transfer the top
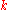 disks to the destination peg, taking
disks to the destination peg, taking 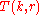 moves.
moves.
The entire process takes
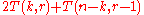 moves. Therefore, the count
moves. Therefore, the count 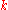 should be picked for which this quantity is minimum.
should be picked for which this quantity is minimum.This algorithm (with the above choice for
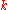 ) is presumed to be optimal, and no counterexamples are known.
) is presumed to be optimal, and no counterexamples are known.Multistack Towers of Hanoi
U.S. patent number 7,566,057 issued to Victor Mascolo discloses multistack Tower of Hanoi puzzles with two or more stacks and twice as many pegs as stacks. After beginning on a particular peg, each stack displaces and is displaced by a different colored stack on another peg when the puzzle is solved. Disks of one color also have another peg that excludes all other colors, so that there are three pegs available for each color disk, two that are shared with other colors, and one that is not shared. On the shared pegs, a disk may not be placed on a different colored disk of the same size, a possibility that does not arise in the standard puzzle.The simplest multistack game, Tower of Hanoi (2 × 4), has two stacks and four pegs, and it requires 3[T(n)] moves to solve where T(n) is the number of moves needed to solve a single stack classic of n disks. The game proceeds in seesaw fashion with longer and longer series of moves that alternate between colors. It concludes in reverse seesaw fashion with shorter and shorter such series of moves. Starting with the second series of three moves, these alternate series of moves double in length for the first half of the game, and the lengths are halved as the game concludes. The solution involves nesting an algorithm suitable for Tower of Hanoi into an algorithm that indicates when to switch between colors. When there are k stacks of n disks apiece in a game, and k > 2, it requires k[T(n)] + T(n − 1) + 1 moves to relocate them.
The addition of a centrally located universal peg open to disks from all stacks converts these multistack Tower of Hanoi puzzles to multistack Reve's puzzles as described in the preceding section. In these games each stack may move among four pegs, the same combination of three in the 2 × 4 game plus the central universal peg. The simplest game of this kind (2 × 5) has two stacks and five pegs. A solution conjectured to be optimal interlocks the optimal solution of the 2 × 4 puzzle with the presumed optimal solution to Reve's puzzle. It takes R(n) + 2R(n − 1) + 2 moves, where R(n) is the number of moves in the presumed optimal Reve's solution for a stack of n disks.
In popular culture
In the classic science fiction story Now Inhale, by Eric Frank RussellEric Frank Russell
Eric Frank Russell was a British author best known for his science fiction novels and short stories. Much of his work was first published in the United States, in John W. Campbell's Astounding Science Fiction and other pulp magazines. Russell also wrote horror fiction for Weird Tales, and...
(Astounding Science Fiction April 1959, and in various anthologies), the human hero is a prisoner on a planet where the local custom is to make the prisoner play a game until it is won or lost, and then execution is immediate. The hero is told the game can be one of his own species', as long as it can be played in his cell with simple equipment strictly according to rules which are written down before and cannot change after play starts, and it has a finite endpoint. The game and execution are televised planet-wide, and watching the desperate prisoner try to spin the game out as long as possible is very popular entertainment; the record is sixteen days. The hero knows a rescue ship might take a year or more to arrive, so chooses to play Towers of Hanoi with 64 disks until rescue arrives. When the locals realize they've been had, they are angry, but under their own rules there is nothing they can do about it. They do change the rules, which will apply to any future prisoners. This story makes reference to the legend about the Buddhist monks playing the game until the end of the world, and refers to the game as arkymalarky. (The slang term "malarky", meaning nonsense, pre-dates this story by at least 30 years. )
In the 1966 Doctor Who
Doctor Who
Doctor Who is a British science fiction television programme produced by the BBC. The programme depicts the adventures of a time-travelling humanoid alien known as the Doctor who explores the universe in a sentient time machine called the TARDIS that flies through time and space, whose exterior...
story The Celestial Toymaker
The Celestial Toymaker
The Celestial Toymaker is a serial in the British science fiction television series Doctor Who, which was first broadcast in four weekly parts from 2 April to 23 April 1966.-Plot:...
, the titular villain forces the Doctor to play a ten-piece 1023-move Tower of Hanoi game entitled The Trilogic Game with the pieces forming a pyramid shape when stacked.
In the 2011 film Rise of the Planet of the Apes the puzzle, named in the film as the "Lucas Tower", was used as a test to study the intelligence of apes.
The puzzle is featured regularly in adventure
Adventure game
An adventure game is a video game in which the player assumes the role of protagonist in an interactive story driven by exploration and puzzle-solving instead of physical challenge. The genre's focus on story allows it to draw heavily from other narrative-based media such as literature and film,...
and puzzle
Computer puzzle game
Puzzle video games are a genre of video games that emphasize puzzle solving. The types of puzzles to be solved can test many problem solving skills including logic, strategy, pattern recognition, sequence solving, and word completion....
games. Since it is easy to implement, and easily recognised, it is well-suited to use as a puzzle in a larger graphical game (e.g. Star Wars: Knights of the Old Republic
Star Wars: Knights of the Old Republic
Star Wars: Knights of the Old Republic is a role-playing video game developed by BioWare and published by LucasArts. It was released for the Xbox on July 15, 2003, for Microsoft Windows on November 19, 2003, and on September 7, 2004 for Mac OS X. The Xbox version is playable on Xbox 360 with its...
and Mass Effect). Some implementations use straight disks, but others disguise the puzzle in some other form.
The problem is featured as part of a reward challenge in a 2011 episode of the American version of the Survivor TV series. Both players (Ozzy Lusth
Ozzy Lusth
Oscar "Ozzy" Lusth is a reality show contestant who first appeared on Survivor: Cook Islands. He finished as the 1st runner-up in a 5–4–0 vote to Yul Kwon. Lusth later competed in Survivor: Micronesia as one of the returning favorites...
and Benjamin "Coach" Wade
Benjamin Wade (Survivor contestant)
Benjamin "Coach" "DragonSlayer" Wade is an American reality television personality best known for being a contestant on Survivor: Tocantins, Survivor: Heroes vs. Villains, and Survivor: South Pacific...
) struggle to understand how to solve the puzzle and are aided by their fellow tribe members.

