Topological defect
Encyclopedia
In mathematics
and physics
, a topological soliton or a topological defect is a solution of a system of partial differential equation
s or of a quantum field theory
homotopically distinct from the vacuum solution
; it can be proven to exist because the boundary conditions entail the existence of homotopically distinct solutions
. Typically, this occurs because the boundary on which the boundary conditions are specified has a non-trivial homotopy group
which is preserved in differential equation
s; the solutions to the differential equations are then topologically distinct, and are classified by their homotopy class. Topological defects are not only stable against small perturbations, but cannot decay or be undone or be de-tangled, precisely because there is no continuous transformation that will map them (homotopically) to a uniform or "trivial" solution.
Examples include the soliton
or solitary wave
which occurs in many exactly solvable models, the screw dislocations in crystalline materials, the skyrmion
and the Wess–Zumino–Witten model in quantum field theory.
Topological defects are believed to drive phase transition
s in condensed matter
physics. Notable examples of topological defects are observed in Lambda transition
universality class systems including: screw/edge-dislocations in liquid crystals, magnetic flux tubes in superconductors, vortices in superfluids.
. According to the Big Bang
theory, the universe cooled from an initial hot, dense state triggering a series of phase transitions much like what happens in condensed-matter systems.
In physical cosmology
, a topological defect is an (often) stable configuration of matter predicted by some theories to form at phase transition
s in the very early universe.
s are believed to have formed in the early universe according to the Higgs–Kibble mechanism. The well-known topological defects are magnetic monopole
s, cosmic string
s, domain wall
s, Skyrmion
s and textures
.
As the universe expanded and cooled, symmetries in the laws of physics began breaking down in regions that spread at the speed of light
; topological defects occur where different regions came into contact with each other. The matter in these defects is in the original symmetric phase, which persists after a phase transition to the new asymmetric new phase is completed.
No topological defects of any type have yet been observed by astronomers, however, and certain types are not compatible with current observations; in particular, if domain walls and monopoles were present in the observable universe, they would result in significant deviations from what astronomers can see. Theories that predict the formation of these structures within the observable universe (see: inflation) can therefore be largely ruled out. On the other hand, cosmic string
s have been suggested as providing the initial 'seed'-gravity around which the large-scale structure of the cosmos of matter has condensed. Textures are similarly benign. In late 2007, a cold spot
in the cosmic microwave background was interpreted as possibly being a sign of a texture
lying in that direction.
Helium
-3.
 that assigns to every point in the region an order parameter, and the possible values of the order parameter space constitute an order parameter space. The homotopy theory of defects uses the fundamental group
that assigns to every point in the region an order parameter, and the possible values of the order parameter space constitute an order parameter space. The homotopy theory of defects uses the fundamental group
of the order parameter space of a medium to discuss the existence, stability and classifications of topological defects in that medium.
Suppose is the order parameter space for a medium, and let
is the order parameter space for a medium, and let 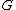 be a Lie group
be a Lie group
of transformations on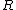 . Let
. Let 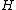 be the symmetry subgroup of
be the symmetry subgroup of 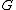 for the medium. Then, the order parameter space can be written as the Lie group quotient
for the medium. Then, the order parameter space can be written as the Lie group quotient 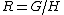
If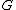 is a universal cover for
is a universal cover for 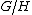 then, it can be shown that
then, it can be shown that 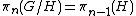 , where
, where 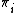 denotes the
denotes the 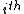 homotopy group
homotopy group
.
Various types of defects in the medium can be characterized by elements of various homotopy groups of the order parameter space. For example, (in three dimensions), line defects correspond to elements of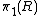 , point defects correspond to elements of
, point defects correspond to elements of 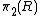 , textures correspond to elements of
, textures correspond to elements of 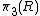 . However, defects which belong to the same conjugacy class
. However, defects which belong to the same conjugacy class
of can be deformed continuously to each other, and hence, distinct defects correspond to distinct conjugacy classes.
can be deformed continuously to each other, and hence, distinct defects correspond to distinct conjugacy classes.
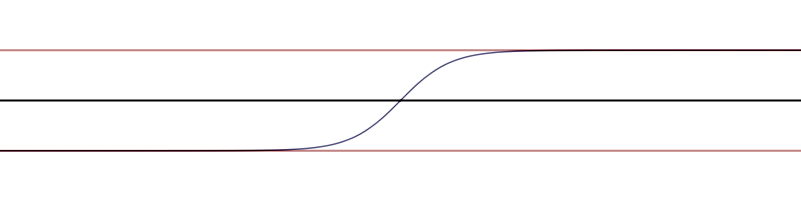
Poénaru and Toulouse showed that crossing defects get entangled if and only if they are members of separate conjugacy classes of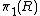

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a topological soliton or a topological defect is a solution of a system of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s or of a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
homotopically distinct from the vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
; it can be proven to exist because the boundary conditions entail the existence of homotopically distinct solutions
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
. Typically, this occurs because the boundary on which the boundary conditions are specified has a non-trivial homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
which is preserved in differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s; the solutions to the differential equations are then topologically distinct, and are classified by their homotopy class. Topological defects are not only stable against small perturbations, but cannot decay or be undone or be de-tangled, precisely because there is no continuous transformation that will map them (homotopically) to a uniform or "trivial" solution.
Examples include the soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
or solitary wave
Solitary wave
In mathematics and physics, a solitary wave can refer to* The solitary wave or wave of translation, as observed by John Scott Russell in the Union Canal, near Edinburgh in 1834...
which occurs in many exactly solvable models, the screw dislocations in crystalline materials, the skyrmion
Skyrmion
In theoretical physics, a skyrmion is a mathematical model used to model baryons . It was conceived by Tony Skyrme.-Overview:...
and the Wess–Zumino–Witten model in quantum field theory.
Topological defects are believed to drive phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s in condensed matter
Condensed Matter
Condensed matter may refer to several things*Condensed matter physics, the study of the physical properties of condensed phases of matter*European Physical Journal B: Condensed Matter and Complex Systems, a scientific journal published by EDP sciences...
physics. Notable examples of topological defects are observed in Lambda transition
Lambda transition
The λ universality class is probably the most important group in condensed matter physics. It regroups several systems possessing strong analogies, namely, superfluids, superconductors and smectics...
universality class systems including: screw/edge-dislocations in liquid crystals, magnetic flux tubes in superconductors, vortices in superfluids.
Cosmology
Certain grand unified theories predict topological defects to have formed in the early universeUniverse
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
. According to the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
theory, the universe cooled from an initial hot, dense state triggering a series of phase transitions much like what happens in condensed-matter systems.
In physical cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
, a topological defect is an (often) stable configuration of matter predicted by some theories to form at phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s in the very early universe.
Symmetry breakdown
Depending on the nature of symmetry breakdown, various solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s are believed to have formed in the early universe according to the Higgs–Kibble mechanism. The well-known topological defects are magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s, cosmic string
Cosmic string
Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking is not simply connected. It is expected that at least one string...
s, domain wall
Domain wall
A domain wall is a term used in physics which can have one of two distinct but similar meanings in magnetism, optics, or string theory. These phenomena can all be generically described as topological solitons which occur whenever a discrete symmetry is spontaneously broken.-Magnetism:In magnetism,...
s, Skyrmion
Skyrmion
In theoretical physics, a skyrmion is a mathematical model used to model baryons . It was conceived by Tony Skyrme.-Overview:...
s and textures
Texture (cosmology)
In cosmology, a texture is a type of topological defect in the structure of spacetime that forms when larger, more complicated symmetry groups are completely broken. They are not as localized as the other defects, and are unstable...
.
As the universe expanded and cooled, symmetries in the laws of physics began breaking down in regions that spread at the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
; topological defects occur where different regions came into contact with each other. The matter in these defects is in the original symmetric phase, which persists after a phase transition to the new asymmetric new phase is completed.
Types of topological defects
Various different types of topological defects are possible, with the type of defect formed being determined by the symmetry properties of the matter and the nature of the phase transition. They include:- Domain wallDomain wallA domain wall is a term used in physics which can have one of two distinct but similar meanings in magnetism, optics, or string theory. These phenomena can all be generically described as topological solitons which occur whenever a discrete symmetry is spontaneously broken.-Magnetism:In magnetism,...
s, two-dimensional membranes that form when a discrete symmetry is broken at a phase transition. These walls resemble the walls of a closed-cell foamFoam-Definition:A foam is a substance that is formed by trapping gas in a liquid or solid in a divided form, i.e. by forming gas regions inside liquid regions, leading to different kinds of dispersed media...
, dividing the universe into discrete cells. - Cosmic stringCosmic stringCosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking is not simply connected. It is expected that at least one string...
s are one-dimensional lines that form when an axial or cylindrical symmetry is broken. - MonopoleMagnetic monopoleA magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s, point-like defects that form when a spherical symmetry is broken, are predicted to have magnetic charge, either north or south (and so are commonly called "magnetic monopoleMagnetic monopoleA magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s"). - Textures form when larger, more complicated symmetry groups are completely broken. They are not as localized as the other defects, and are unstable. Other more complex hybrids of these defect types are also possible.
- Extra-dimensions and higher dimensionsDimensionsDimensions is a French project that makes educational movies about mathematics, focusing on spatial geometry. It uses POV-Ray to render some of the animations, and the films are release under a Creative Commons licence....
.
Observation
Topological defects, of the cosmological type, are extremely high-energy phenomena and are likely impossible to produce in artificial Earth-bound physics experiments, but topological defects that formed during the universe's formation could theoretically be observed.No topological defects of any type have yet been observed by astronomers, however, and certain types are not compatible with current observations; in particular, if domain walls and monopoles were present in the observable universe, they would result in significant deviations from what astronomers can see. Theories that predict the formation of these structures within the observable universe (see: inflation) can therefore be largely ruled out. On the other hand, cosmic string
Cosmic string
Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking is not simply connected. It is expected that at least one string...
s have been suggested as providing the initial 'seed'-gravity around which the large-scale structure of the cosmos of matter has condensed. Textures are similarly benign. In late 2007, a cold spot
WMAP cold spot
The CMB Cold Spot or WMAP Cold Spot is a region of the sky seen in microwaves which analysis found to be unusually large and cold relative to the expected properties of the cosmic microwave background radiation...
in the cosmic microwave background was interpreted as possibly being a sign of a texture
Texture (cosmology)
In cosmology, a texture is a type of topological defect in the structure of spacetime that forms when larger, more complicated symmetry groups are completely broken. They are not as localized as the other defects, and are unstable...
lying in that direction.
Condensed matter
In condensed matter physics, the theory of homotopy groups provides a natural setting for description and classification of defects in ordered systems. Topological methods have been used in several problems of condensed matter theory. Poénaru and Toulouse used topological methods to obtain a condition for line (string) defects in liquid crystals can cross each other without entanglement. It was a non-trivial application of topology that first led to the discovery of peculiar hydrodynamic behavior in the A-phase of superfluidSuperfluid
Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...
Helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
-3.
Classification
An ordered medium is defined as a region of space described by a function that assigns to every point in the region an order parameter, and the possible values of the order parameter space constitute an order parameter space. The homotopy theory of defects uses the fundamental group
that assigns to every point in the region an order parameter, and the possible values of the order parameter space constitute an order parameter space. The homotopy theory of defects uses the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the order parameter space of a medium to discuss the existence, stability and classifications of topological defects in that medium.
Suppose
 is the order parameter space for a medium, and let
is the order parameter space for a medium, and let 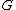 be a Lie group
be a Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of transformations on
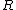 . Let
. Let 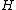 be the symmetry subgroup of
be the symmetry subgroup of 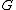 for the medium. Then, the order parameter space can be written as the Lie group quotient
for the medium. Then, the order parameter space can be written as the Lie group quotient 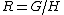
If
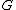 is a universal cover for
is a universal cover for 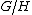 then, it can be shown that
then, it can be shown that 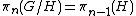 , where
, where 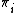 denotes the
denotes the 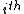 homotopy group
homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
.
Various types of defects in the medium can be characterized by elements of various homotopy groups of the order parameter space. For example, (in three dimensions), line defects correspond to elements of
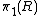 , point defects correspond to elements of
, point defects correspond to elements of 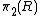 , textures correspond to elements of
, textures correspond to elements of 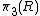 . However, defects which belong to the same conjugacy class
. However, defects which belong to the same conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
of
 can be deformed continuously to each other, and hence, distinct defects correspond to distinct conjugacy classes.
can be deformed continuously to each other, and hence, distinct defects correspond to distinct conjugacy classes.Poénaru and Toulouse showed that crossing defects get entangled if and only if they are members of separate conjugacy classes of
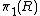
Stable defects
Unlike in cosmology and field theory, topological defects in condensed matter can be experimentally observed. Ferromagnetic materials have regions of magnetic alignment separated by domain walls. Nematic and bi-axial nematic liquid crystals display a variety of defects including monopoles, strings, textures etc. Defects can also been found in biochemistry, notably in the process of protein folding.Images


See also
- quantum vortexQuantum vortexIn physics, a quantum vortex is a topological defect exhibited in superfluids and superconductors. Superfluids and superconductors are states of matter without friction. They exist only at very low temperatures. The existence of these quantum vortices was independently predicted by Richard Feynman...
- dislocationDislocationIn materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
- vector solitonVector solitonIn physical optics or wave optics, a vector soliton is a solitary wave with multiple components coupled together that maintains its shape during propagation. Ordinary solitons maintain their shape but have effectively only one polarization component, while vector solitons have two distinct...
- Quantum topologyQuantum topologyQuantum topology is a branch of mathematics that connects quantum mechanics with low-dimensional topology.Dirac notation provides a viewpoint of quantum mechanics which becomes amplified into a framework that can embrace the amplitudes associated with topological spaces and the related embedding of...
- Topological entropy in physics
- Topological orderTopological orderIn physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
- Topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
- Topological quantum numberTopological quantum numberIn physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...
- Topological string theoryTopological string theoryIn theoretical physics, topological string theory is a simplified version of string theory. The operators in topological string theory represent the algebra of operators in the full string theory that preserve a certain amount of supersymmetry...
External links
- Cosmic Strings & other Topological Defects
- http://demonstrations.wolfram.com/SeparationOfTopologicalSingularities/

