Topkis's Theorem
Encyclopedia
In mathematical economics
, Topkis's theorem is a result that is useful for establishing comparative statics
. The theorem allows researchers to understand how the optimal value for a choice variable changes when a feature of the environment changes. The result states that if f is supermodular
in (x,θ), and D is a lattice
, then
is nondecreasing in θ. The result is especially helpful for establishing comparative static results when the objective function is not differentiable.
A driver is driving down a highway and must choose a speed, s. Going faster is desirable, but is more likely to result in a crash. There is some prevalence of potholes, p. The presence of potholes increases the probability crashing. Note that s is a choice variable and p is a parameter of the environment that is fixed from the perspective of the driver. The driver seeks to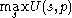
.
We would like to understand how the driver's speed (a choice variable) changes with the amount of potholes:
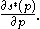
If one wanted to solve the problem with standard tools such as the implicit function theorem
, one would have to assume that the problem is well behaved: U(.) is twice continuously differentiable, concave in s, that the domain over which s is defined is convex, and that it there is a unique maximizer
for every value of p and that 
is in the interior of the set over which s is defined. Note that the optimal speed is a function of the amount of potholes. Taking the first order condition, we know that at the optimum,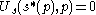 
. Differentiating the first order condition, with respect to p and using the implicit function theorem, we find that
or that
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
, Topkis's theorem is a result that is useful for establishing comparative statics
Comparative statics
In economics, comparative statics is the comparison of two different economic outcomes, before and after a change in some underlying exogenous parameter....
. The theorem allows researchers to understand how the optimal value for a choice variable changes when a feature of the environment changes. The result states that if f is supermodular
Supermodular
In mathematics, a functionf\colon R^k \to Ris supermodular iff + f \geq f + ffor all x, y \isin Rk, where x \vee y denotes the componentwise maximum and x \wedge y the componentwise minimum of x and y.If −f is supermodular then f is called submodular, and if the inequality is changed to an...
in (x,θ), and D is a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
, then
is nondecreasing in θ. The result is especially helpful for establishing comparative static results when the objective function is not differentiable.An example
This example will show how using Topkis's Theorem gives the same result as using more standard tools. The advantage of using Topkis's Theorem is that it can be applied to a wider class of problems than can be studied with standard economics tools.A driver is driving down a highway and must choose a speed, s. Going faster is desirable, but is more likely to result in a crash. There is some prevalence of potholes, p. The presence of potholes increases the probability crashing. Note that s is a choice variable and p is a parameter of the environment that is fixed from the perspective of the driver. The driver seeks to
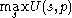.We would like to understand how the driver's speed (a choice variable) changes with the amount of potholes:
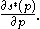
If one wanted to solve the problem with standard tools such as the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
, one would have to assume that the problem is well behaved: U(.) is twice continuously differentiable, concave in s, that the domain over which s is defined is convex, and that it there is a unique maximizer
for every value of p and that is in the interior of the set over which s is defined. Note that the optimal speed is a function of the amount of potholes. Taking the first order condition, we know that at the optimum, 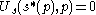. Differentiating the first order condition, with respect to p and using the implicit function theorem, we find that
or that
-
So,
If s and p are substitutes,
and hence
and more potholes causes less speeding. Clearly it is more reasonable to assume that they are substitutes.
The problem with the above approach is that it relies on the differentiability of the objective function and on concavity. We could get at the same answer using Topkis's Theorem in the following way. We want to show that
is submodular (the opposite of supermodular) in 
. Note that the choice set is clearly a lattice. The cross partial of U being negative,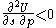 
, is a sufficient condition. Hence if 
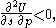we know that 
.
Hence using the implicit function theoremImplicit function theoremIn multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
and Topkis's theorem gives the same result, but the latter does so with fewer assumptions.