
Toda bracket
Encyclopedia
In mathematics, the Toda bracket is an operation on homotopy classes of maps, in particular on homotopy groups of spheres
, named after Hiroshi Toda
who defined them and used them to compute homotopy groups of spheres in .
Suppose that
is a sequence of maps between space, such that gf and hg are both nullhomotopic. Given a space A, let CA denote the cone of A. Then we get a non-unique map from CW to Y from a homotopy from gf to a trivial map, which when composed with h gives a map from CW to Z. Similarly we get a non-unique map from CX to Z from a homotopy from hg to a trivial map, which when composed with Cf, the cone of the map f, gives another map from CW to Z. By joining together these two cones on W and the maps from them to Z, we get a map 〈f, g, h〉 in the group [SW, Z] of homotopy classes of maps from the suspension SW to Z, called the Toda bracket of f, g, and h. It is not uniquely defined up to homotopy, because there was some choice in choosing the maps from the cones. Changing these maps changes the Toda bracket by adding elements of h[SW,Y] and [SX,Z]f.
There are also higher Toda brackets of several elements, defined when suitable lower Toda brackets vanish. This parallels the theory of Massey product
s in cohomology
.
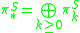
of the stable homotopy groups of spheres is a supercommutative graded ring
, where multiplication (called composition product) is given by composition of representing maps, and any element of non-zero degree is nilpotent
.
If f and g and h are elements of π∗S with f ⋅ g = 0 and g ⋅ h = 0, there is a Toda bracket 〈f, g, h〉 of these elements. The Toda bracket is not quite an element of a stable homotopy group, because it is only defined up to addition of composition products of certain other elements. Hiroshi Toda
used the composition product and Toda brackets to label many of the elements of homotopy groups.
showed that every element of the stable homotopy groups of spheres can be expressed using composition products and higher Toda brackets in terms of certain well known elements, called Hopf elements.
Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
, named after Hiroshi Toda
Hiroshi Toda
is a Japanese mathematician, who specializes in stable and unstable homotopy theory.He started publishing in 1952. Many of his early papers are concerned with the study of Whitehead products and their behaviour under suspension and more generally with the homotopy groups of spheres. In a 1957...
who defined them and used them to compute homotopy groups of spheres in .
Definition
See or for more information.Suppose that

is a sequence of maps between space, such that gf and hg are both nullhomotopic. Given a space A, let CA denote the cone of A. Then we get a non-unique map from CW to Y from a homotopy from gf to a trivial map, which when composed with h gives a map from CW to Z. Similarly we get a non-unique map from CX to Z from a homotopy from hg to a trivial map, which when composed with Cf, the cone of the map f, gives another map from CW to Z. By joining together these two cones on W and the maps from them to Z, we get a map 〈f, g, h〉 in the group [SW, Z] of homotopy classes of maps from the suspension SW to Z, called the Toda bracket of f, g, and h. It is not uniquely defined up to homotopy, because there was some choice in choosing the maps from the cones. Changing these maps changes the Toda bracket by adding elements of h[SW,Y] and [SX,Z]f.
There are also higher Toda brackets of several elements, defined when suitable lower Toda brackets vanish. This parallels the theory of Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
s in cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
The Toda bracket stable for homotopy groups of spheres
The direct sum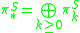
of the stable homotopy groups of spheres is a supercommutative graded ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, where multiplication (called composition product) is given by composition of representing maps, and any element of non-zero degree is nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
.
If f and g and h are elements of π∗S with f ⋅ g = 0 and g ⋅ h = 0, there is a Toda bracket 〈f, g, h〉 of these elements. The Toda bracket is not quite an element of a stable homotopy group, because it is only defined up to addition of composition products of certain other elements. Hiroshi Toda
Hiroshi Toda
is a Japanese mathematician, who specializes in stable and unstable homotopy theory.He started publishing in 1952. Many of his early papers are concerned with the study of Whitehead products and their behaviour under suspension and more generally with the homotopy groups of spheres. In a 1957...
used the composition product and Toda brackets to label many of the elements of homotopy groups.
showed that every element of the stable homotopy groups of spheres can be expressed using composition products and higher Toda brackets in terms of certain well known elements, called Hopf elements.

