Timeline of Islamic science and technology
Encyclopedia
This timeline of science
and engineering
in the Islamic world
covers the time period from the 7th century AD to the introduction of European
science
to the Islamic world in the 19th and 20th centuries. All year dates are given according to the Gregorian calendar
except where noted.
in the 19th and 20th centuries, the concept of Islamic science rapidly loses significance.
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
in the Islamic world
Muslim world
The term Muslim world has several meanings. In a religious sense, it refers to those who adhere to the teachings of Islam, referred to as Muslims. In a cultural sense, it refers to Islamic civilization, inclusive of non-Muslims living in that civilization...
covers the time period from the 7th century AD to the introduction of European
History of Europe
History of Europe describes the history of humans inhabiting the European continent since it was first populated in prehistoric times to present, with the first human settlement between 45,000 and 25,000 BC.-Overview:...
science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
to the Islamic world in the 19th and 20th centuries. All year dates are given according to the Gregorian calendar
Gregorian calendar
The Gregorian calendar, also known as the Western calendar, or Christian calendar, is the internationally accepted civil calendar. It was introduced by Pope Gregory XIII, after whom the calendar was named, by a decree signed on 24 February 1582, a papal bull known by its opening words Inter...
except where noted.
8th century
- 8th - 9th century - [cosmetics] Ziriyab (Blackbird) starts a beauty institute in Spain.
- 770 - 840 - [mathematics] Kharazmi (Persian: خوارزمي, in Arabic became الخوارزمي al-Khwarizmi, Latinized name, Algorithm). Developed the "calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
of resolution and juxtaposition" (hisab al-jabr w'al-muqabala), more briefly referred to as al-jabr, or algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
- 776 - 868 - [zoology; language] 'Amr ibn Bahr Al-JahizAl-JahizAl-Jāḥiẓ was an Arabic prose writer and author of works of literature, Mu'tazili theology, and politico-religious polemics.In biology, Al-Jahiz introduced the concept of food chains and also proposed a scheme of animal evolution that entailed...
. ZoologyZoologyZoology |zoölogy]]), is the branch of biology that relates to the animal kingdom, including the structure, embryology, evolution, classification, habits, and distribution of all animals, both living and extinct...
, Arabic grammarArabic grammarArabic grammar is the grammar of the Arabic language. Arabic is a Semitic language and its grammar has many similarities with the grammar of other Semitic languages....
, rhetoricRhetoricRhetoric is the art of discourse, an art that aims to improve the facility of speakers or writers who attempt to inform, persuade, or motivate particular audiences in specific situations. As a subject of formal study and a productive civic practice, rhetoric has played a central role in the Western...
, lexicographyLexicographyLexicography is divided into two related disciplines:*Practical lexicography is the art or craft of compiling, writing and editing dictionaries....
.
- late 8th century - early 9th century - [music] Mansour Zalzal of Kufa. Musician (luth) and composer of the AbbasidAbbasidThe Abbasid Caliphate or, more simply, the Abbasids , was the third of the Islamic caliphates. It was ruled by the Abbasid dynasty of caliphs, who built their capital in Baghdad after overthrowing the Umayyad caliphate from all but the al-Andalus region....
era. Contributed musical scaleMusical scaleIn music, a scale is a sequence of musical notes in ascending and descending order. Most commonly, especially in the context of the common practice period, the notes of a scale will belong to a single key, thus providing material for or being used to conveniently represent part or all of a musical...
s that were later named after him (the Mansouri scale) and introduced positions (intervals) within scales such as the wasati-zalzal that was equidistantEquidistantA point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.In two-dimensional Euclidian geometry the locus of points equidistant from two given points is their perpendicular bisector...
from the alwasati alqadima and wasati al-fors. Made improvements on the design of the luth instrument and designed the Luth. Teacher of Is-haq al-Mawsili.
9th century
- 800 - 873 - [various] Ibn Ishaq Al-KindiAl-Kindi' , known as "the Philosopher of the Arabs", was a Muslim Arab philosopher, mathematician, physician, and musician. Al-Kindi was the first of the Muslim peripatetic philosophers, and is unanimously hailed as the "father of Islamic or Arabic philosophy" for his synthesis, adaptation and promotion...
(latinized, Alkindus.) PhilosophyPhilosophyPhilosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
, Physics, Optics, Medicine, Mathematics, Cryptography, MetallurgyMetallurgyMetallurgy is a domain of materials science that studies the physical and chemical behavior of metallic elements, their intermetallic compounds, and their mixtures, which are called alloys. It is also the technology of metals: the way in which science is applied to their practical use...
. Worked at the House of WisdomHouse of WisdomThe House of Wisdom was a library and translation institute established in Abbassid-era Baghdad, Iraq. It was a key institution in the Translation Movement and considered to have been a major intellectual centre during the Islamic Golden Age...
which was set up in 810.
- 803 - [chemistry; glass] d. Abu-Moussa Jabir ibn Hayyan (Latinized name, Geber,). Famous Persian chemist. First chemist known to produce sulfuric acidSulfuric acidSulfuric acid is a strong mineral acid with the molecular formula . Its historical name is oil of vitriol. Pure sulfuric acid is a highly corrosive, colorless, viscous liquid. The salts of sulfuric acid are called sulfates...
, as well as many other chemicals and instruments. Wrote on adding color to glass by adding small quantities of metallic oxideOxideAn oxide is a chemical compound that contains at least one oxygen atom in its chemical formula. Metal oxides typically contain an anion of oxygen in the oxidation state of −2....
s to the glassGlassGlass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...
, such as manganese dioxide (magnesiaMagnesium oxideMagnesium oxide , or magnesia, is a white hygroscopic solid mineral that occurs naturally as periclase and is a source of magnesium . It has an empirical formula of and consists of a lattice of Mg2+ ions and O2– ions held together by ionic bonds...
). This was a new advancement in glass industry unknown in antiquity. His works include "The elaboration of the Grand Elixir"; "The chest of wisdom" in which he writes on nitric acidNitric acidNitric acid , also known as aqua fortis and spirit of nitre, is a highly corrosive and toxic strong acid.Colorless when pure, older samples tend to acquire a yellow cast due to the accumulation of oxides of nitrogen. If the solution contains more than 86% nitric acid, it is referred to as fuming...
; Kitab al-istitmam (translated to Latin later as Summa Perfectionis); and others.
- ca. 810 Bayt al-Hikma (House of WisdomHouse of WisdomThe House of Wisdom was a library and translation institute established in Abbassid-era Baghdad, Iraq. It was a key institution in the Translation Movement and considered to have been a major intellectual centre during the Islamic Golden Age...
) set up in Baghdad. There GreekGreek languageGreek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
and IndiaIndiaIndia , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
n mathematical and astronomy works are translated into ArabicArabic languageArabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
.
- 820 - [mathematics] Mahani (full name Abu Abdollah Muhammad ibn Isa Mahani - in Arabic Al-MahaniAl-MahaniAbu-Abdullah Muhammad ibn Īsa Māhānī was a Persian mathematician and astronomer from Mahan, Kermān, Persia.A series of observations of lunar and solar eclipses and planetary conjunctions, made by him from 853 to 866, was in fact used by Ibn Yunus....
). Conceived the idea of reducing geometrical problems such as duplicating the cube to problems in algebra. [1]
- 836 - 901 [anatomy; astronomy; mathematics; mechanics] Born Thabit Ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
(latinized, Thebit.) Studied at Baghdad's House of Wisdom under the Banu MusaBanu MusaThe Banū Mūsā brothers , namely Abū Jaʿfar Muḥammad ibn Mūsā ibn Shākir , Abū al‐Qāsim Aḥmad ibn Mūsā ibn Shākir and Al-Ḥasan ibn Mūsā ibn Shākir , were three 9th-century Persian scholars of Baghdad who are known for their Book of Ingenious Devices on automata and mechanical devices...
brothers. Made many contributions to mathematics, particularly in geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. He discovered the theorem by which pairs of amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s can be found; i.e., two numbers such that each is the sum of the proper divisors of the other.[1] Later, al-Baghdadi (b. 980) and al-Haytham (born 965) developed variants of the theorem.
- 838 - 870 - Tabari (full name: Ali ibn Sahl Rabban Al-TabariAli ibn Sahl Rabban al-TabariAbu al-Hasan Ali ibn Sahl Rabban al-Tabari also given as 810-855 and 783-858 was a Persian Muslim hakim, Islamic scholar, physician and psychologist of Zoroastrian descent, who produced one of the first encyclopedia of medicine. He was a pioneer of pediatrics and the field of child development...
). Medicine, Mathematics, CalligraphyCalligraphyCalligraphy is a type of visual art. It is often called the art of fancy lettering . A contemporary definition of calligraphic practice is "the art of giving form to signs in an expressive, harmonious and skillful manner"...
, Literature. [4]
- mid 9th century - [chemistry] Al-KindiAl-Kindi' , known as "the Philosopher of the Arabs", was a Muslim Arab philosopher, mathematician, physician, and musician. Al-Kindi was the first of the Muslim peripatetic philosophers, and is unanimously hailed as the "father of Islamic or Arabic philosophy" for his synthesis, adaptation and promotion...
writes on the distillationDistillationDistillation is a method of separating mixtures based on differences in volatilities of components in a boiling liquid mixture. Distillation is a unit operation, or a physical separation process, and not a chemical reaction....
of wineWineWine is an alcoholic beverage, made of fermented fruit juice, usually from grapes. The natural chemical balance of grapes lets them ferment without the addition of sugars, acids, enzymes, or other nutrients. Grape wine is produced by fermenting crushed grapes using various types of yeast. Yeast...
as that of rose water and gives 107 recipes for perfumePerfumePerfume is a mixture of fragrant essential oils and/or aroma compounds, fixatives, and solvents used to give the human body, animals, objects, and living spaces "a pleasant scent"...
s, in his book Kitab Kimia al-`otoor wa al-tas`eedat (book of the chemistry of perfumes and distillations.)
- 850 - 930 [mathematics] born Abu KamilAbu Kamil' was an Egyptian Muslim mathematician during the Islamic Golden Age...
of Egypt (full name, Abu Kamil Shuja ibn Aslam ibn Muhammad ibn Shuja) Forms an important link in the development of algebra between al-Khwarizmi and al-KarajiAl-Karaji' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
. Despite not using symbols, but writing powers of x in words, he had begun to understand what we would write in symbols as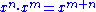
.[1]
- 858 - 929 - [astronomy - mathematics] Al-BattaniAl-BattaniAbū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī al-Ṣābiʾ al-Battānī was a Muslim astronomer, astrologer, and mathematician...
(Albategnius) Works on astronomy, trigonometry etc.
- ca. 860 - Al-FarghaniAl-Farghani' also known as Alfraganus in the West was a Persian astronomer and one of the famous astronomers in 9th century. The crater Alfraganus on the Moon is named after him.-Life:...
(Al-Fraganus) Astronomy, Civil engineeringCivil engineeringCivil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
.
- 864 - 930 - [chemistry; medicine; ...] RaziAl-RaziMuhammad ibn Zakariyā Rāzī , known as Rhazes or Rasis after medieval Latinists, was a Persian polymath,a prominent figure in Islamic Golden Age, physician, alchemist and chemist, philosopher, and scholar....
(Rhazes) Medicine, OphthalmologyOphthalmologyOphthalmology is the branch of medicine that deals with the anatomy, physiology and diseases of the eye. An ophthalmologist is a specialist in medical and surgical eye problems...
, SmallpoxSmallpoxSmallpox was an infectious disease unique to humans, caused by either of two virus variants, Variola major and Variola minor. The disease is also known by the Latin names Variola or Variola vera, which is a derivative of the Latin varius, meaning "spotted", or varus, meaning "pimple"...
, Chemistry, Astronomy. Al-Razi wrote on Naft (naphta or petroleumPetroleumPetroleum or crude oil is a naturally occurring, flammable liquid consisting of a complex mixture of hydrocarbons of various molecular weights and other liquid organic compounds, that are found in geologic formations beneath the Earth's surface. Petroleum is recovered mostly through oil drilling...
) and its distillates in his book "Kitab sirr al-asrar" (book of the secret of secrets.) When choosing a site to build Baghdad's hospital, he hung pieces of fresh meat in different parts of the city. The location where the meat took the longest to rotDecompositionDecomposition is the process by which organic material is broken down into simpler forms of matter. The process is essential for recycling the finite matter that occupies physical space in the biome. Bodies of living organisms begin to decompose shortly after death...
was the one he chose for building the hospital. Advocated that patients not be told their real condition so that fearFearFear is a distressing negative sensation induced by a perceived threat. It is a basic survival mechanism occurring in response to a specific stimulus, such as pain or the threat of danger...
or despair do not affect the healingHealingPhysiological healing is the restoration of damaged living tissue, organs and biological system to normal function. It is the process by which the cells in the body regenerate and repair to reduce the size of a damaged or necrotic area....
process. Wrote on alkaliAlkaliIn chemistry, an alkali is a basic, ionic salt of an alkali metal or alkaline earth metal element. Some authors also define an alkali as a base that dissolves in water. A solution of a soluble base has a pH greater than 7. The adjective alkaline is commonly used in English as a synonym for base,...
, caustic soda, soapSoapIn chemistry, soap is a salt of a fatty acid.IUPAC. "" Compendium of Chemical Terminology, 2nd ed. . Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford . XML on-line corrected version: created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN...
and glycerine. Gave descriptions of equipment processes and methods in his book Kitab al-Asrar (book of secrets) in 925.
- 870 - 950 - Farabi (Al-Pharabius) SociologySociologySociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, LogicLogicIn philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, PhilosophyPhilosophyPhilosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
, Political sciencePolitical sciencePolitical Science is a social science discipline concerned with the study of the state, government and politics. Aristotle defined it as the study of the state. It deals extensively with the theory and practice of politics, and the analysis of political systems and political behavior...
, Music.
- 888 - [various] Died 'Abbas Ibn FirnasAbbas Ibn FirnasAbbas Ibn Firnas , also known as Abbas Qasim Ibn Firnas and عباس بن فرناس , was a Muslim Andalusian polymath: an inventor, engineer, aviator, physician, Arabic poet, and Andalusian musician. Of Berber descent, he was born in Izn-Rand Onda, Al-Andalus , and lived in the Emirate of Córdoba...
. Mechanics of FlightFlightFlight is the process by which an object moves either through an atmosphere or beyond it by generating lift or propulsive thrust, or aerostatically using buoyancy, or by simple ballistic movement....
, PlanetariumPlanetariumA planetarium is a theatre built primarily for presenting educational and entertaining shows about astronomy and the night sky, or for training in celestial navigation...
, Artificial Crystals. Ibn Firnas investigated means of flight and was apparently injured due to a trial in which he attempted to fly off of a cliff using wings. One of the earliest records of attempts at flight.
- 9th century - [chemistry; petroleum] Oilfields in BakuBakuBaku , sometimes spelled as Baki or Bakou, is the capital and largest city of Azerbaijan, as well as the largest city on the Caspian Sea and of the Caucasus region. It is located on the southern shore of the Absheron Peninsula, which projects into the Caspian Sea. The city consists of two principal...
, AzerbaijanAzerbaijanAzerbaijan , officially the Republic of Azerbaijan is the largest country in the Caucasus region of Eurasia. Located at the crossroads of Western Asia and Eastern Europe, it is bounded by the Caspian Sea to the east, Russia to the north, Georgia to the northwest, Armenia to the west, and Iran to...
, generate commercial activities and industry. These oilfields, were wells are dug to get the Naft (or naphta, or crude petroleumPetroleumPetroleum or crude oil is a naturally occurring, flammable liquid consisting of a complex mixture of hydrocarbons of various molecular weights and other liquid organic compounds, that are found in geologic formations beneath the Earth's surface. Petroleum is recovered mostly through oil drilling...
) are described by geographer Masudi in the 10th century and by Marco PoloMarco PoloMarco Polo was a Venetian merchant traveler from the Venetian Republic whose travels are recorded in Il Milione, a book which did much to introduce Europeans to Central Asia and China. He learned about trading whilst his father and uncle, Niccolò and Maffeo, travelled through Asia and apparently...
in the 13th century, who described the output of those wells as hundreds of shiploads.
10th century
- 10th century [mathematics; accounting] By this century, three systems of countingNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
are used in the Arab world. Finger-reckoning arithmetic, with numerals written entirely in words, used by the business community; the sexagesimal system, a remnant originating with the Babylonians, with numerals denoted by letters of the arabic alphabetArabic alphabetThe Arabic alphabet or Arabic abjad is the Arabic script as it is codified for writing the Arabic language. It is written from right to left, in a cursive style, and includes 28 letters. Because letters usually stand for consonants, it is classified as an abjad.-Consonants:The Arabic alphabet has...
and used by Arab mathematicians in astronomical work; and the indian numeral systemIndian numeralsMost of the positional base 10 numeral systems in the world have originated from India, where the concept of positional numeration was first developed...
, which was used with various sets of symbols [1]. Its arithmetic at first required the use of a dust board (a sort of handheld blackboardBlackboardA chalkboard is a reusable writing surface.Blackboard may also refer to:* Blackboards are synonymous with "boards of infamy", an element of agitation-propaganda in the Soviet Union in 1930s, coincidental with Holodomor...
) because "the methods required moving the numbers around in the calculation and rubbing some out as the calculation proceeded." Al-Uqlidisi (born 920) modified these methods for pen and paper use [1].
- 903 - 986 [astronomy] Al-Sufi (latinized name, Azophi).
- 920 [mathematics] Born al-Uqlidisi. Modified arithmetic methods for the Indian numeral system to make it possible for pen and paper use. Hitherto, doing calculations with the Indian numerals necessitated the use of a dust board as noted earlier.
- 936 - 1013 [medicine] Al-Zahrawi (latinized name, Albucasis) SurgerySurgerySurgery is an ancient medical specialty that uses operative manual and instrumental techniques on a patient to investigate and/or treat a pathological condition such as disease or injury, or to help improve bodily function or appearance.An act of performing surgery may be called a surgical...
, Medicine. Called the "Father of Modern Surgery." [4]
- 940 - 997 [astronomy; mathematics] Muhammad Al-Buzjani. Mathematics, Astronomy, Geometry, Trigonometry.
- 940 [mathematics] Born Abu'l-Wafa al-Buzjani. Wrote several treatiseTreatiseA treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject.-Noteworthy treatises:...
s using the finger-counting system of arithmetic, and was also an expert on the Indian numerals system. About the Indian system he wrote: "[it] did not find application in business circles and among the population of the Eastern CaliphateCaliphateThe term caliphate, "dominion of a caliph " , refers to the first system of government established in Islam and represented the political unity of the Muslim Ummah...
for a long time." [1] Using the Indian numeral system, abu'l Wafa was able to extract rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s.
- 953 [mathematics] Born al-KarajiAl-Karaji' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
of Karaj and Baghdad (full name, Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji or al-Karkhi). Believed to be the "first person to completely free algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
from geometrical operations and to replace them with the arithmetical type of operations which are at the core of algebra today. He was first to define the monomialMonomialIn mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s
, 
, 
, ... and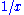 
, 
, 
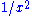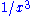, ... and to give rules for productsProduct (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of any two of these. He started a school of algebra which flourished for several hundreds of years" [1]. Discovered the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
for integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
exponents. [1] states that this "was a major factor in the development of numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
based on the decimal system."
- 957 [geography; cartography; exploration; chemistry] died Abul Hasan Ali Al-Masudi, best known as a cartographer, was also a traveler historian, etc. Al-mas`oudi described his visit to the oilfields of BakuBakuBaku , sometimes spelled as Baki or Bakou, is the capital and largest city of Azerbaijan, as well as the largest city on the Caspian Sea and of the Caucasus region. It is located on the southern shore of the Absheron Peninsula, which projects into the Caspian Sea. The city consists of two principal...
. Wrote on the reaction of alkali water with zaj (vitriol) water giving sulfuric acidSulfuric acidSulfuric acid is a strong mineral acid with the molecular formula . Its historical name is oil of vitriol. Pure sulfuric acid is a highly corrosive, colorless, viscous liquid. The salts of sulfuric acid are called sulfates...
.
- 965 - 1040 [mathematics; optics; physics] Born ibn al-HaithamIbn al-Haitham' was a Muslim, scientist and polymath described in various sources as either Arabic or Persian...
(full name, ; latinized name, Alhazen). Possibly the first to classify all even perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s (i.e., numbers equal to the sum of their proper divisors) as those of the form
where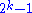 
is prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
[1]. Al-Haytham is also the first person to state Wilson's theorem. if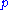
is prime than 
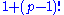is divisible by 
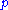. [1] says "It is called Wilson's theorem because of a comment by Waring in 1770 that John Wilson had noticed the result. There is no evidence that Wilson knew how to prove it. It was over 750 years later that LagrangeJoseph Louis LagrangeJoseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
gave the first known proof to the statement in 1771.[1]
- 972 - 1058 [humanities] Al-MawardiAl-MawardiAbu al-Hasan Ali Ibn Muhammad Ibn Habib al-Mawardi , known in Latin as Alboacen , was an Arab Muslim jurist of the Shafi'i school most remembered for his works on religion, government, the caliphate, and public and constitutional law during a time of political turmoil...
(Alboacen) Political sciencePolitical sciencePolitical Science is a social science discipline concerned with the study of the state, government and politics. Aristotle defined it as the study of the state. It deals extensively with the theory and practice of politics, and the analysis of political systems and political behavior...
, SociologySociologySociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, JurisprudenceJurisprudenceJurisprudence is the theory and philosophy of law. Scholars of jurisprudence, or legal theorists , hope to obtain a deeper understanding of the nature of law, of legal reasoning, legal systems and of legal institutions...
, EthicsEthicsEthics, also known as moral philosophy, is a branch of philosophy that addresses questions about morality—that is, concepts such as good and evil, right and wrong, virtue and vice, justice and crime, etc.Major branches of ethics include:...
.
- 973 - 1048 [mathematics; physics] Abu Raihan Al-BiruniAl-BiruniAbū al-Rayḥān Muḥammad ibn Aḥmad al-BīrūnīArabic spelling. . The intermediate form Abū Rayḥān al-Bīrūnī is often used in academic literature...
; Astronomy, Mathematics. Determined Earth's circumference.
- 980 [mathematics] Born al-Baghdadi (full name). Studied a slight variant of Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
's theorem on amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s.[1] Al-Baghdadi also wrote texts comparing the three systems of counting and arithmetic used in the region during this period. Made improvements on the decimal system.
- 981 - 1037 [astronomy; mathematics; medicine; philosophy] Ibn Sina (Avicenna); Medicine, Philosophy, Mathematics, Astronomy
11th century
- 1044 or 1048 - 1123 [mathematics] Omar Al-Khayyam. Persian mathematician and poet. "Gave a complete classification of cubic equations with geometric solutions found by means of intersecting conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s. Khayyam also wrote that he hoped to give a full description of the algebraic solution of cubic equations in a later work: 'If the opportunity arises and I can succeed, I shall give all these fourteen forms with all their branches and cases, and how to distinguish whatever is possible or impossible so that a paper, containing elements which are greatly useful in this art will be prepared.' " [1]. Extracted rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s using the decimal system (the Indian numeral system). There is dispute whether the MaqamatMaqamat Badi' az-Zaman al-HamadhaniMaqamat Badi' al-Zaman al-Hamadhani, , an Arabic collection from the 9th century of 400 episodic stories, roughly 52 of which have survived. A century later, these maqamat inspired the maqamat of Al-Hariri of Basra, which in turn inspired the Hebrew Tahkemoni.-External links:** English translation...
, a famous diwan of poetry translated to English are actually his work.
- 1058 - 1111 [law; theology] Al-GhazaliAl-GhazaliAbu Hāmed Mohammad ibn Mohammad al-Ghazzālī , known as Algazel to the western medieval world, born and died in Tus, in the Khorasan province of Persia was a Persian Muslim theologian, jurist, philosopher, and mystic....
(Algazel), judge and prolific thinker and writer on topis such as sociologySociologySociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, theologyTheologyTheology is the systematic and rational study of religion and its influences and of the nature of religious truths, or the learned profession acquired by completing specialized training in religious studies, usually at a university or school of divinity or seminary.-Definition:Augustine of Hippo...
and philosophyPhilosophyPhilosophy is the study of general and fundamental problems, such as those connected with existence, knowledge, values, reason, mind, and language. Philosophy is distinguished from other ways of addressing such problems by its critical, generally systematic approach and its reliance on rational...
. He critiqued the so-called Greek philosophers Ibn Sina, aka Avicenna and al-FarabiAl-Farabi' known in the West as Alpharabius , was a scientist and philosopher of the Islamic world...
, aka Farabius. Wrote extensive expositions on Islamic tenets and foundations of jurisprudenceJurisprudenceJurisprudence is the theory and philosophy of law. Scholars of jurisprudence, or legal theorists , hope to obtain a deeper understanding of the nature of law, of legal reasoning, legal systems and of legal institutions...
. Also critiqued the Muslim scholastics (al-mutakallimun.) Was associated with sufismSufismSufism or ' is defined by its adherents as the inner, mystical dimension of Islam. A practitioner of this tradition is generally known as a '...
but he later critiqued it as well.
- 1091 - 1161 [medicine] Ibn ZuhrIbn ZuhrAbū Merwān ’Abdal-Malik ibn Zuhr was a Muslim physician, surgeon and teacher in Al-Andalus.He was born at Seville...
(Avenzoar) Surgery, Medicine.
- 1099 - 1166 [cartography;geography] Muhammad Al-IdrisiMuhammad al-IdrisiAbu Abd Allah Muhammad al-Idrisi al-Qurtubi al-Hasani al-Sabti or simply Al Idrisi was a Moroccan Muslim geographer, cartographer, Egyptologist and traveller who lived in Sicily, at the court of King Roger II. Muhammed al-Idrisi was born in Ceuta then belonging to the Almoravid Empire and died in...
(Dreses)
12th century
- 1100 - 1166 (AH 493 - 560) [cartography, geography] Muhammad al-Idrissi, aka Idris al-Saqalli aka al-sharif al-idrissi of AndalusiaAndalusiaAndalusia is the most populous and the second largest in area of the autonomous communities of Spain. The Andalusian autonomous community is officially recognised as a nationality of Spain. The territory is divided into eight provinces: Huelva, Seville, Cádiz, Córdoba, Málaga, Jaén, Granada and...
and SicilySicilySicily is a region of Italy, and is the largest island in the Mediterranean Sea. Along with the surrounding minor islands, it constitutes an autonomous region of Italy, the Regione Autonoma Siciliana Sicily has a rich and unique culture, especially with regard to the arts, music, literature,...
. Known for having drawn some of the most advanced ancient world maps, as well as writing on travels and geography.
- 1106 - 1138 [polymath] Abu Bakr Muhammad Ibn Yahya (Ibn BajjahIbn BajjahAbū-Bakr Muhammad ibn Yahya ibn al-Sāyigh , known as Ibn Bājjah , was an Andalusian polymath: an astronomer, logician, musician, philosopher, physician, physicist, psychologist, botanist, poet and scientist. He was known in the West by his Latinized name, Avempace...
) Philosophy, Medicine, Mathematics, Astronomy, Poetry, Music.
- 1110 - 1185 [literature, philosophy] Abdubacer Ibn Tufayl of Spain. Philosophy, medicine, poetry, fiction. His most famous work is Hayy ibn Yaqzan, which is a spiritual investigation into the reality of the world narrated by a man who was raised from infancy by a roe or gazelle.
- 1128 - 1198 [philosophy] Ibn Rushd (Averroes) Philosophy, Law, Medicine, Astronomy, Theology.
- 1130 [mathematics] Born al-SamawalAl-Samawal' commonly known as Samau'al al-Maghribi was a Muslim mathematician, astronomer and physician of Jewish descent. Though born to a Jewish family, he converted to Islam in 1163 after he had a dream telling him to do so...
. An important member of al-Karaji's school of algebra. Gave this definition of algebra: "[it is concerned] with operating on unknowns using all the arithmetical tools, in the same way as the arithmetician operates on the known." [1]
- 1135 [mathematics] Born Sharafeddin TusiSharafeddin Tusi' was a Persian mathematician and astronomer of the Islamic Golden Age .- Biography :...
. Follows al-Khayyam's application of algebra of geometry, rather than follow the general development that came through al-Karaji's school of algebra. Wrote a treatise on cubic equations which [3] describes thus: "[the treatise] represents an essential contribution to another algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
which aimed to study curveCurveIn mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s by means of equationEquationAn equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s, thus inaugurating the beginning of algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
." (quoted in [1]).
13th century
- 13th century - [medicine; scientific method] Ibn Al-NafisAl-NafisAla-al-din abu Al-Hassan Ali ibn Abi-Hazm al-Qarshi al-Dimashqi , known as Ibn al-Nafis , was an Arab physician who is mostly famous for being the first to describe the pulmonary circulation of the blood.He was born in 1213 in Damascus...
b. ca. 607AH, d. ca. 689AH. DamasceneDamascusDamascus , commonly known in Syria as Al Sham , and as the City of Jasmine , is the capital and the second largest city of Syria after Aleppo, both are part of the country's 14 governorates. In addition to being one of the oldest continuously inhabited cities in the world, Damascus is a major...
physician and anatomist. Discovered the lesser circulatory systemCirculatory systemThe circulatory system is an organ system that passes nutrients , gases, hormones, blood cells, etc...
(the cycle involving the ventricleVentricle (heart)In the heart, a ventricle is one of two large chambers that collect and expel blood received from an atrium towards the peripheral beds within the body and lungs. The Atria primes the Pump...
s of the heartHeartThe heart is a myogenic muscular organ found in all animals with a circulatory system , that is responsible for pumping blood throughout the blood vessels by repeated, rhythmic contractions...
and the lungs), and described the mechanism of breathingBreathingBreathing is the process that moves air in and out of the lungs. Aerobic organisms require oxygen to release energy via respiration, in the form of the metabolism of energy-rich molecules such as glucose. Breathing is only one process that delivers oxygen to where it is needed in the body and...
and its relation to the bloodBloodBlood is a specialized bodily fluid in animals that delivers necessary substances such as nutrients and oxygen to the cells and transports metabolic waste products away from those same cells....
and how it nourishes on air in the lungs. Followed a "constructivist" path of the smaller circulatory system: "blood is purified in the lungs for the continuance of life and providing the body with the ability to work". During his time, the common view was that blood originates in the liver then travels to the right ventricle, then on to the organs of the body; another contemporary view was that blood is filtered through the diaphragm where it mixes with the air coming from the lungs. Ibn al-Nafis discredited all these views including ones by GalenGalenAelius Galenus or Claudius Galenus , better known as Galen of Pergamon , was a prominent Roman physician, surgeon and philosopher...
and AvicennaAvicennaAbū ʿAlī al-Ḥusayn ibn ʿAbd Allāh ibn Sīnā , commonly known as Ibn Sīnā or by his Latinized name Avicenna, was a Persian polymath, who wrote almost 450 treatises on a wide range of subjects, of which around 240 have survived...
(ibn Sina). At least an illustration of his manuscript is still extant. William HarveyWilliam HarveyWilliam Harvey was an English physician who was the first person to describe completely and in detail the systemic circulation and properties of blood being pumped to the body by the heart...
explained the circulatory system without reference to ibn al-Nafis in 1628. Ibn al-Nafis extolled the study of comparative anatomy in his "Explaining the dissection of [Avicenna's] Al-QanoonAl-QanoonAl-Qanoon is the name of a monthly magazine in Pakistan. The name al-Qanoon when translated from Arabic to English means "The Law".Al-Qanoon is the first legal magazine of the country also containing political and legal chapters from the famous advocates and analysts of the country.It is owned...
" which includes a prefaces, and citations of sources. Emphasized the rigours of verification by measurement, observation and experiment. Subjected conventional wisdom of his time to a critical review and verified it with experiment and observation, discarding errors.
- 13th century - [chemistry] Al-Jawbari describes the preparation of rose water in the work "Book of Selected Disclosure of Secrets" (Kitab kashf al-Asrar).
- 13th century - [chemistry; materials; glassmaking] Arabic manuscript on the manufacture of false gemstoneGemstoneA gemstone or gem is a piece of mineral, which, in cut and polished form, is used to make jewelry or other adornments...
s and diamonds. Also describes spirits of alumAlumAlum is both a specific chemical compound and a class of chemical compounds. The specific compound is the hydrated potassium aluminium sulfate with the formula KAl2.12H2O. The wider class of compounds known as alums have the related empirical formula, AB2.12H2O.-Chemical properties:Alums are...
, spirits of saltpetrePotassium nitratePotassium nitrate is a chemical compound with the formula KNO3. It is an ionic salt of potassium ions K+ and nitrate ions NO3−.It occurs as a mineral niter and is a natural solid source of nitrogen. Its common names include saltpetre , from medieval Latin sal petræ: "stone salt" or possibly "Salt...
and spirits of salts (hydrochloric acidHydrochloric acidHydrochloric acid is a solution of hydrogen chloride in water, that is a highly corrosive, strong mineral acid with many industrial uses. It is found naturally in gastric acid....
).
- 13th century - [chemistry] An Arabic manuscript written in syriac script gives description of various chemical materials and their properties such as sulfuric acidSulfuric acidSulfuric acid is a strong mineral acid with the molecular formula . Its historical name is oil of vitriol. Pure sulfuric acid is a highly corrosive, colorless, viscous liquid. The salts of sulfuric acid are called sulfates...
, sal-ammoniac, saltpetrePotassium nitratePotassium nitrate is a chemical compound with the formula KNO3. It is an ionic salt of potassium ions K+ and nitrate ions NO3−.It occurs as a mineral niter and is a natural solid source of nitrogen. Its common names include saltpetre , from medieval Latin sal petræ: "stone salt" or possibly "Salt...
and zaj (vitriol).
- 1201 - 1274 - [astronomy; mathematics] Nasir Al-Din Al-TusiNasir al-Din al-TusiKhawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
; Astronomy, Non-Euclidean geometryNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
.
- 1204 [astronomy] Died, Al-Bitruji (Alpetragius.)
- 1207 - 1273 [sociology; poetry; spirituality] Jalal al-Din Muhammad Rumi, one of the best known persian passion poets, famous for poignant poetry on the theme of spiritual enlightenmentEnlightenment (concept)Enlightenment broadly means wisdom or understanding enabling clarity of perception. However, the English word covers two concepts which can be quite distinct: religious and spiritual enlightenment and secular or intellectual enlightenment...
and passion.
- 1213 - 1288[anatomy] Ibn Al-NafisAl-NafisAla-al-din abu Al-Hassan Ali ibn Abi-Hazm al-Qarshi al-Dimashqi , known as Ibn al-Nafis , was an Arab physician who is mostly famous for being the first to describe the pulmonary circulation of the blood.He was born in 1213 in Damascus...
al-Damishqui.
- 1248 - [pharmacy; veterinary medicine] Died Ibn Al-BaitarAl-BaitarIbn al-Bayṭār al-Mālaqī, Ḍiyāʾ Al-Dīn Abū Muḥammad ʿAbdllāh Ibn Aḥmad was an Andalusian scientist, botanist, pharmacist and physician who worked during the Islamic Golden Age and Arab Agricultural Revolution...
. Studied and wrote on botanyBotanyBotany, plant science, or plant biology is a branch of biology that involves the scientific study of plant life. Traditionally, botany also included the study of fungi, algae and viruses...
, pharmacyPharmacyPharmacy is the health profession that links the health sciences with the chemical sciences and it is charged with ensuring the safe and effective use of pharmaceutical drugs...
and is best known for studying animal anatomy and medicine. The Arabic term for veterinary medicine is named after him.
- 1260 [mathematics] Born al-FarisiAl-FarisiKamal al-Din Hasan ibn Ali ibn Hasan Farisi or Abu Hasan Muhammad ibn Hasan ) was a prominent Persian born in Tabriz, Iran. He made two major contributions to science, one on optics, the other on number theory...
. Gave a new proof of Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
's theorem, introducing important new ideas concerning factorizationFactorizationIn mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
and combinatorial methods. He also gave the pair of amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s 17296, 18416 which have also been joint attributed to Fermat as well as Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
.
- 1273 - 1331 [astronomy; geography; history] Abu al-Fida (Abulfeda).
14th century
- 1301 - [ceramics] Al-Kashani promotes a center for ceramics. He also writes a book on Islamic ceramicsCeramics (art)In art history, ceramics and ceramic art mean art objects such as figures, tiles, and tableware made from clay and other raw materials by the process of pottery. Some ceramic products are regarded as fine art, while others are regarded as decorative, industrial or applied art objects, or as...
techniques. His name is still associated with ceramics in the Muslim OrientOrientThe Orient means "the East." It is a traditional designation for anything that belongs to the Eastern world or the Far East, in relation to Europe. In English it is a metonym that means various parts of Asia.- Derivation :...
today.
- 1304 - 1369 [exploration; travel] Abu Abdullah Muhammad ibn BattutaIbn BattutaAbu Abdullah Muhammad Ibn Battuta , or simply Ibn Battuta, also known as Shams ad–Din , was a Muslim Moroccan Berber explorer, known for his extensive travels published in the Rihla...
; World Traveler. 75,000 mile voyage from MoroccoMoroccoMorocco , officially the Kingdom of Morocco , is a country located in North Africa. It has a population of more than 32 million and an area of 710,850 km², and also primarily administers the disputed region of the Western Sahara...
to ChinaChinaChinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
and back.
- 1332 - 1395 [history; political science; humanities] Ibn KhaldunIbn KhaldunIbn Khaldūn or Ibn Khaldoun was an Arab Tunisian historiographer and historian who is often viewed as one of the forerunners of modern historiography, sociology and economics...
. Sociology, Philosophy of History, general science, Political Science. His most famous work, al-Muqqadima (Prolegomena), encyclopedic in breadth, surveys the state of knowledge of his day, covering geography, accounts of the peoples of the world and their known history, the classification and aims of the sciences and the religious sciences.
- 1380 [mathematics] Born al-Kashi. According to [1], "contributed to the development of decimal fractions not only for approximating algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, but also for real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s such as piPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
. His contribution to decimal fractions is so major that for many years he was considered as their inventor. Although not the first to do so, al-Kashi gave an algorithm for calculating nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
s which is a special case of the methods given many centuries later by RuffiniPaolo RuffiniPaolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...
and HornerWilliam George HornerWilliam George Horner was a British mathematician and schoolmaster. The invention of the zoetrope, in 1834 and under a different name , has been attributed to him.-Life:...
."
- 1393 - 1449 - [astronomy] Ulugh BegUlugh BegUlugh Bek was a Timurid ruler as well as an astronomer, mathematician and sultan. His commonly-known name is not truly a personal name, but rather a moniker, which can be loosely translated as "Great Ruler" or "Patriarch Ruler" and was the Turkic equivalent of Timur's Perso-Arabic title Amīr-e...
commissions an observatory at Samarqand in present-day UzbekistanUzbekistanUzbekistan , officially the Republic of Uzbekistan is a doubly landlocked country in Central Asia and one of the six independent Turkic states. It shares borders with Kazakhstan to the west and to the north, Kyrgyzstan and Tajikistan to the east, and Afghanistan and Turkmenistan to the south....
.
15th century
- 15th century [mathematics] Ibn al-Banna and al-Qalasadi used symbols for mathematics in the 15th century "and, although we do not know exactly when their use began, we know that symbols were used at least a century before this." [1]
- 15th century - [astronomy and mathematics] Ibn Masoud (Ghayyathuddin Jamshid ibn mohamed ibn mas`oud, d. 1424 or 1436.) First to use the decimal point in arithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
. Wrote on the decimal system. First to introduce the zero0 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
(indian mathematicians had used only nine glyphs for numerals). Computed and observed the solar eclipseSolar eclipseAs seen from the Earth, a solar eclipse occurs when the Moon passes between the Sun and the Earth, and the Moon fully or partially blocks the Sun as viewed from a location on Earth. This can happen only during a new moon, when the Sun and the Moon are in conjunction as seen from Earth. At least...
s of 809AH, 810AH and 811AH, after being invited by Ulugh Bek, based in Samarqand to pursue his study of mathematics, astronomy and physics. His works include "The Key of arithmetics"; "Discoveries in mathematics"; "The Decimal point"; "the benefits of the zero". The contents of the Benefits of the Zero are an introduction followed by five essays: On whole number arithmetic; On fractional arithmetic; on astrology; on areas; on finding the unknowns [unknown variables]. He also wrote a "Thesis on the sine and the chord"; "thesis on the circumference" in which he found the ratio of the circumferenceCircumferenceThe circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
to the radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
to the 16th decimal; "The garden of gardens" or "promenade of the gardens" describing an instrument he devised and used at the Samarqand observatoryObservatoryAn observatory is a location used for observing terrestrial or celestial events. Astronomy, climatology/meteorology, geology, oceanography and volcanology are examples of disciplines for which observatories have been constructed...
to compile an ephemerisEphemerisAn ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
, and for computing solar and lunar eclipseLunar eclipseA lunar eclipse occurs when the Moon passes behind the Earth so that the Earth blocks the Sun's rays from striking the Moon. This can occur only when the Sun, Earth, and Moon are aligned exactly, or very closely so, with the Earth in the middle. Hence, a lunar eclipse can only occur the night of a...
s; The ephemeresis "Zayj Al-Khaqani" which also includes mathematical tables and corrections of the ephemeresis by Al-Tusi; "Thesis on finding the first degree sine"; and more.
- 1411 [mathematics] Al-Kashi writes Compendium of the Science of Astronomy [5].
- 1424 [mathematics] Al-Kashi writes Treatise on the Circumference giving a remarkably good approximation to pi in both sexagesimal and decimalDecimalThe decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
forms [5].
- 1427 [mathematics] Al-Kashi completes The Key to Arithmetic containing work of great depth on decimal fractions. It applies arithmetical and algebraic methods to the solution of various problems, including several geometric ones and is one of the best textbooks in the whole of medieval literature [5].
- 1437 [mathematics] Ulugh BegUlugh BegUlugh Bek was a Timurid ruler as well as an astronomer, mathematician and sultan. His commonly-known name is not truly a personal name, but rather a moniker, which can be loosely translated as "Great Ruler" or "Patriarch Ruler" and was the Turkic equivalent of Timur's Perso-Arabic title Amīr-e...
publishes his star catalogueStar catalogueA star catalogue, or star catalog, is an astronomical catalogue that lists stars. In astronomy, many stars are referred to simply by catalogue numbers. There are a great many different star catalogues which have been produced for different purposes over the years, and this article covers only some...
Zij-i Sultani. It contains trigonometric tablesGenerating trigonometric tablesIn mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering...
correct to eight decimal places based on Ulugh Beg's calculation of the sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of one degree which he calculated correctly to 16 decimal places [5].
17th century
- 17th century [mathematics] The Arabic mathematician Mohammed Baqir Yazdi joint discovered the pair of amicable numberAmicable numberAmicable numbers are two different numbers so related that the sum of the proper divisors of each is equal to the other number. A pair of amicable numbers constitutes an aliquot sequence of period 2...
s 9,363,584 and 9,437,056 along with Descartes (1636).
18th century
- 1783 - 1799 - [rocketry] TipuTipu SultanTipu Sultan , also known as the Tiger of Mysore, was the de facto ruler of the Kingdom of Mysore. He was the son of Hyder Ali, at that time an officer in the Mysorean army, and his second wife, Fatima or Fakhr-un-Nissa...
, SultanSultanSultan is a title with several historical meanings. Originally, it was an Arabic language abstract noun meaning "strength", "authority", "rulership", and "dictatorship", derived from the masdar سلطة , meaning "authority" or "power". Later, it came to be used as the title of certain rulers who...
of Mysore [1783-1799] in the south of IndiaIndiaIndia , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
, was an experimentator with war rocketRocketA rocket is a missile, spacecraft, aircraft or other vehicle which obtains thrust from a rocket engine. In all rockets, the exhaust is formed entirely from propellants carried within the rocket before use. Rocket engines work by action and reaction...
s. Two of his rockets, captured by the British at Srirangapatana, are displayed in the WoolwichWoolwichWoolwich is a district in south London, England, located in the London Borough of Greenwich. The area is identified in the London Plan as one of 35 major centres in Greater London.Woolwich formed part of Kent until 1889 when the County of London was created...
Royal Artillery Museum in LondonLondonLondon is the capital city of :England and the :United Kingdom, the largest metropolitan area in the United Kingdom, and the largest urban zone in the European Union by most measures. Located on the River Thames, London has been a major settlement for two millennia, its history going back to its...
. The rocket motor casing was made of steel with multiple nozzles. The rocket, 50 mm in diameter and 250 mm long, had a range performance of 900 meters to 1.5 km. (src: http://www.cyberistan.org/islamic/).
19th century
With the adoption of European scienceScience
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
in the 19th and 20th centuries, the concept of Islamic science rapidly loses significance.
External links
- "How Greek Science Passed to the Arabs" by De Lacy O'Leary
- 1001 Inventions