
Theory of computation
Encyclopedia
In theoretical computer science
, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation
, using an algorithm
. The field is divided into three major branches: automata theory
, computability theory
and computational complexity theory
.
In order to perform a rigorous study of computation, computer scientists work with a mathematical abstraction of computers called a model of computation. There are several models in use, but the most commonly examined is the Turing machine
. Computer scientists study the Turing machine because it is simple to formulate, can be analyzed and used to prove results, and because it represents what many consider the most powerful possible "reasonable" model of computation. It might seem that the potentially infinite memory capacity is an unrealizable attribute, but any decidable
problem solved by a Turing machine will always require only a finite amount of memory. So in principle, any problem that can be solved (decided) by a Turing machine can be solved by a computer that has a bounded amount of memory.
Some pioneers of the theory of computation were Alonzo Church
, Alan Turing
, Stephen Kleene, John von Neumann
, Claude Shannon, and Noam Chomsky
.
Automata theory is also closely related to formal language theory, as the automata are often classified by the class of formal languages they are able to recognize. An automaton can be a finite representation of a formal language that may be an infinite set.
cannot be solved by a Turing machine is one of the most important results in computability theory, as it is an example of a concrete problem that is both easy to formulate and impossible to solve using a Turing machine. Much of computability theory builds on the halting problem result.
Another important step in computability theory was Rice's theorem
, which states that for all non-trivial properties of partial functions, it is undecidable whether a Turing machine computes a partial function with that property.
Computability theory is closely related to the branch of mathematical logic
called recursion theory
, which removes the restriction of studying only models of computation which are reducible to the Turing model. Many mathematicians and computational theorists who study recursion theory will refer to it as computability theory.
considers not only whether a problem can be solved at all on a computer, but also how efficiently the problem can be solved. Two major aspects are considered: time complexity and space complexity, which are respectively how many steps does it take to perform a computation, and how much memory is required to perform that computation.
In order to analyze how much time and space a given algorithm
requires, computer scientists express the time or space required to solve the problem as a function of the size of the input problem. For example, finding a particular number in a long list of numbers becomes harder as the list of numbers grows larger. If we say there are n numbers in the list, then if the list is not sorted or indexed in any way we may have to look at every number in order to find the number we're seeking. We thus say that in order to solve this problem, the computer needs to perform a number of steps that grows linearly in the size of the problem.
To simplify this problem, computer scientists have adopted Big O notation
, which allows functions to be compared in a way that ensures that particular aspects of a machine's construction do not need to be considered, but rather only the asymptotic behavior as problems become large. So in our previous example we might say that the problem requires steps to solve.
steps to solve.
Perhaps the most important open problem in all of computer science is the question of whether a certain broad class of problems denoted NP
can be solved efficiently. This is discussed further at Complexity classes P and NP.
, other equivalent (See: Church–Turing thesis
) models of computation are in use.
Lambda calculus
: A computation consists of an initial lambda expression (or two if you want to separate the function and its input) plus a finite sequence of lambda terms, each deduced from the preceding term by one application of Beta reduction.
Combinatory logic
mu-recursive function
s: a computation consists of a mu-recursive function, i.e. its defining sequence, any input value(s) and a sequence of recursive functions appearing in the defining sequence with inputs and outputs. Thus, if in the defining sequence of a recursive function the functions
the functions  and
and 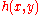 appear, then terms of the form 'g(5)=7' or 'h(3,2)=10' might appear. Each entry in this sequence needs to be an application of a basic function or follow from the entries above by using composition
appear, then terms of the form 'g(5)=7' or 'h(3,2)=10' might appear. Each entry in this sequence needs to be an application of a basic function or follow from the entries above by using composition
, primitive recursion or mu recursion
. For instance if , then for 'f(5)=3' to appear, terms like 'g(5)=6' and 'h(5,6)=3' must occur above. The computation terminates only if the final term gives the value of the recursive function applied to the inputs.
, then for 'f(5)=3' to appear, terms like 'g(5)=6' and 'h(5,6)=3' must occur above. The computation terminates only if the final term gives the value of the recursive function applied to the inputs.
Markov algorithm
: a string rewriting system that uses grammar
-like rules to operate on strings
of symbols.
Register machine
P′′
In addition to the general computational models, some simpler computational models are useful for special, restricted applications. Regular expressions, for example, specify string patterns in many contexts, from office productivity software to programming language
s. Another formalism mathematically equivalent to regular expressions, Finite automata are used in circuit design and in some kinds of problem-solving. Context-free grammar
s specify programming language syntax. Non-deterministic pushdown automata
are another formalism equivalent to context-free grammars. Primitive recursive function
s are a defined subclass of the recursive functions.
Different models of computation have the ability to do different tasks. One way to measure the power of a computational model is to study the class of formal language
s that the model can generate; in such a way to the Chomsky hierarchy
of languages is obtained.
(There are many textbooks in this area; this list is by necessity incomplete.)
Books on computability theory from the (wider) mathematical perspective
Historical perspective.
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
, using an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. The field is divided into three major branches: automata theory
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
, computability theory
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
and computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
.
In order to perform a rigorous study of computation, computer scientists work with a mathematical abstraction of computers called a model of computation. There are several models in use, but the most commonly examined is the Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
. Computer scientists study the Turing machine because it is simple to formulate, can be analyzed and used to prove results, and because it represents what many consider the most powerful possible "reasonable" model of computation. It might seem that the potentially infinite memory capacity is an unrealizable attribute, but any decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
problem solved by a Turing machine will always require only a finite amount of memory. So in principle, any problem that can be solved (decided) by a Turing machine can be solved by a computer that has a bounded amount of memory.
History
The theory of computation can be considered the creation of models of all kinds in the field of computer science. Therefore mathematics and logic are used. In the last century it became an independent academic discipline and was separated from mathematics.Some pioneers of the theory of computation were Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
, Stephen Kleene, John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, Claude Shannon, and Noam Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
.
Automata theory
Automata theory is the study of abstract machines (or more appropriately, abstract 'mathematical' machines or systems) and the computational problems that can be solved using these machines. These abstract machines are called automata. Automata comes from the Greek word (Αυτόματα) which means that something is doing something by itself.Automata theory is also closely related to formal language theory, as the automata are often classified by the class of formal languages they are able to recognize. An automaton can be a finite representation of a formal language that may be an infinite set.
Computability theory
Computability theory deals primarily with the question of the extent to which a problem is solvable on a computer. The statement that the halting problemHalting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
cannot be solved by a Turing machine is one of the most important results in computability theory, as it is an example of a concrete problem that is both easy to formulate and impossible to solve using a Turing machine. Much of computability theory builds on the halting problem result.
Another important step in computability theory was Rice's theorem
Rice's theorem
In computability theory, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide whether an algorithm computes a partial function with that property...
, which states that for all non-trivial properties of partial functions, it is undecidable whether a Turing machine computes a partial function with that property.
Computability theory is closely related to the branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
called recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, which removes the restriction of studying only models of computation which are reducible to the Turing model. Many mathematicians and computational theorists who study recursion theory will refer to it as computability theory.
Computational complexity theory
Complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
considers not only whether a problem can be solved at all on a computer, but also how efficiently the problem can be solved. Two major aspects are considered: time complexity and space complexity, which are respectively how many steps does it take to perform a computation, and how much memory is required to perform that computation.
In order to analyze how much time and space a given algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
requires, computer scientists express the time or space required to solve the problem as a function of the size of the input problem. For example, finding a particular number in a long list of numbers becomes harder as the list of numbers grows larger. If we say there are n numbers in the list, then if the list is not sorted or indexed in any way we may have to look at every number in order to find the number we're seeking. We thus say that in order to solve this problem, the computer needs to perform a number of steps that grows linearly in the size of the problem.
To simplify this problem, computer scientists have adopted Big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, which allows functions to be compared in a way that ensures that particular aspects of a machine's construction do not need to be considered, but rather only the asymptotic behavior as problems become large. So in our previous example we might say that the problem requires
 steps to solve.
steps to solve.Perhaps the most important open problem in all of computer science is the question of whether a certain broad class of problems denoted NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
can be solved efficiently. This is discussed further at Complexity classes P and NP.
Models of computation
Aside from a Turing machineTuring machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, other equivalent (See: Church–Turing thesis
Church–Turing thesis
In computability theory, the Church–Turing thesis is a combined hypothesis about the nature of functions whose values are effectively calculable; in more modern terms, algorithmically computable...
) models of computation are in use.
Lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
: A computation consists of an initial lambda expression (or two if you want to separate the function and its input) plus a finite sequence of lambda terms, each deduced from the preceding term by one application of Beta reduction.
Combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
- is a concept which has many similarities to
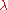 -calculus, but also important differences exist (e.g. fixed point combinator Y has normal form in combinatory logic but not in
-calculus, but also important differences exist (e.g. fixed point combinator Y has normal form in combinatory logic but not in  -calculus). Combinatory logic was developed with great ambitions: understanding the nature of paradoxes, making foundations of mathematics more economic (conceptually), eliminating the notion of variables (thus clarifying their role in mathematics).
-calculus). Combinatory logic was developed with great ambitions: understanding the nature of paradoxes, making foundations of mathematics more economic (conceptually), eliminating the notion of variables (thus clarifying their role in mathematics).
mu-recursive function
Mu-recursive function
In mathematical logic and computer science, the μ-recursive functions are a class of partial functions from natural numbers to natural numbers which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that...
s: a computation consists of a mu-recursive function, i.e. its defining sequence, any input value(s) and a sequence of recursive functions appearing in the defining sequence with inputs and outputs. Thus, if in the defining sequence of a recursive function
 the functions
the functions  and
and 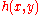 appear, then terms of the form 'g(5)=7' or 'h(3,2)=10' might appear. Each entry in this sequence needs to be an application of a basic function or follow from the entries above by using composition
appear, then terms of the form 'g(5)=7' or 'h(3,2)=10' might appear. Each entry in this sequence needs to be an application of a basic function or follow from the entries above by using compositionFunction composition (computer science)
In computer science, function composition is an act or mechanism to combine simple functions to build more complicated ones...
, primitive recursion or mu recursion
Mu-recursive function
In mathematical logic and computer science, the μ-recursive functions are a class of partial functions from natural numbers to natural numbers which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that...
. For instance if
 , then for 'f(5)=3' to appear, terms like 'g(5)=6' and 'h(5,6)=3' must occur above. The computation terminates only if the final term gives the value of the recursive function applied to the inputs.
, then for 'f(5)=3' to appear, terms like 'g(5)=6' and 'h(5,6)=3' must occur above. The computation terminates only if the final term gives the value of the recursive function applied to the inputs.Markov algorithm
Markov algorithm
In theoretical computer science, a Markov algorithm is a string rewriting system that uses grammar-like rules to operate on strings of symbols. Markov algorithms have been shown to be Turing-complete, which means that they are suitable as a general model of computation and can represent any...
: a string rewriting system that uses grammar
Grammar
In linguistics, grammar is the set of structural rules that govern the composition of clauses, phrases, and words in any given natural language. The term refers also to the study of such rules, and this field includes morphology, syntax, and phonology, often complemented by phonetics, semantics,...
-like rules to operate on strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
of symbols.
Register machine
Register machine
In mathematical logic and theoretical computer science a register machine is a generic class of abstract machines used in a manner similar to a Turing machine...
- is a theoretically interesting idealization of a computer. There are several variants. In most of them, each register can hold a natural number (of unlimited size), and the instructions are simple (and few in number), e.g. only decrementation (combined with conditional jump) and incrementation exist (and halting). The lack of the infinite (or dynamically growing) external store (seen at Turing machines) can be understood by replacing its role with Gödel numbering techniques: the fact that each register holds a natural number allows the possibility of representing a complicated thing (e.g. a sequence, or a matrix etc.) by an appropriate huge natural number — unambiguity of both representation and interpretation can be established by number theoreticalNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
foundations of these techniques.
P′′
- Like Turing machines, P′′ uses an infinite tape of symbols (without random access), and a rather minimalistic set of instructions. But these instructions are very different, thus, unlike Turing machines, P′′ does not need to maintain a distinct state, because all “memory-like” functionality can be provided only by the tape. Instead of rewriting the current symbol, it can perform a modular arithmeticModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
incrementation on it. P′′ has also a pair of instructions for a cycle, inspecting the blank symbol. Despite its minimalistic nature, it has become the parental formal language of an implemented and (for entertainment) used programming language called BrainfuckBrainfuckThe brainfuck programming language is an esoteric programming language noted for its extreme minimalism. It is a Turing tarpit, designed to challenge and amuse programmers, and is not suitable for practical use...
.
In addition to the general computational models, some simpler computational models are useful for special, restricted applications. Regular expressions, for example, specify string patterns in many contexts, from office productivity software to programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s. Another formalism mathematically equivalent to regular expressions, Finite automata are used in circuit design and in some kinds of problem-solving. Context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s specify programming language syntax. Non-deterministic pushdown automata
Pushdown automaton
In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
are another formalism equivalent to context-free grammars. Primitive recursive function
Primitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
s are a defined subclass of the recursive functions.
Different models of computation have the ability to do different tasks. One way to measure the power of a computational model is to study the class of formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s that the model can generate; in such a way to the Chomsky hierarchy
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
of languages is obtained.
Further reading
Textbooks aimed at computer scientists(There are many textbooks in this area; this list is by necessity incomplete.)
- Hopcroft, John E.John HopcroftJohn Edward Hopcroft is an American theoretical computer scientist. His textbooks on theory of computation and data structures are regarded as standards in their fields. He is the IBM Professor of Engineering and Applied Mathematics in Computer Science at Cornell University.He received his...
, and Jeffrey D. Ullman (2006). Introduction to Automata Theory, Languages, and ComputationIntroduction to Automata Theory, Languages, and ComputationIntroduction to Automata Theory, Languages, and Computation, is an influential computer science textbook by John Hopcroft and Jeffrey Ullman on formal languages and the theory of computation.- Nickname :...
. 3rd ed Reading, MA: Addison-Wesley. ISBN 978-0321455369 One of the standard references in the field. - Hein, James L. (1996) Theory of Computation. Sudbury, MA: Jones & Bartlett. ISBN 978-0867204971 A gentle introduction to the field, appropriate for second-year undergraduate computer science students.
- Taylor, R. Gregory (1998). Models of Computation and Formal Languages. New York: Oxford University Press. ISBN 978-0195109832 An unusually readable textbook, appropriate for upper-level undergraduates or beginning graduate students.
- Lewis, F. D. (2007). Essentials of theoretical computer science A textbook covering the topics of formal languages, automata and grammars. The emphasis appears to be on presenting an overview of the results and their applications rather than providing proofs of the results.
- Martin DavisMartin DavisMartin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, Ron Sigal, Elaine J. Weyuker, Computability, complexity, and languages: fundamentals of theoretical computer science, 2nd ed., Academic Press, 1994, ISBN 0122063821. Covers a wider range of topics than most other introductory books, including program semantics and quantification theory. Aimed at graduate students.
Books on computability theory from the (wider) mathematical perspective
- Hartley Rogers, JrHartley Rogers, JrHartley Rogers, Jr. is a mathematician who has worked in recursion theory, and who is currently a professor in the Mathematics Department of the Massachusetts Institute of Technology. The Rogers equivalence theorem is named after him....
(1987). Theory of Recursive Functions and Effective Computability, MIT Press. ISBN 0-262-68052-1. - Carl H. Smith, A recursive introduction to the theory of computation, Springer, 1994, ISBN 0387943323. A shorter textbook suitable for graduate students in Computer Science.
Historical perspective.
External links
- Computability Logic - A theory of interactive computation. The main web source on this subject.

