
Teleparallelism
Encyclopedia
Teleparallelism was an attempt by Einstein
to unify electromagnetism
and gravity. The idea is to use a geometry with a pseudo-Riemannian metric of signature
(3,1), vanishing curvature
, and non-vanishing torsion
, and to use tetrad
s, rather than the metric, as basic variables.
Nowadays, people study teleparallelism purely as a theory of gravity without trying to unify it with electromagnetism.
If this choice is made, then there is no longer any Lorentz gauge symmetry and the internal Minkowski space
fiber is now global. However, a translational gauge symmetry may be introduced thus: Instead of seeing tetrads as fundamental, we introduce a fundamental R4 translational gauge symmetry instead (which acts upon the internal Minkowski space fibers affine
ly so that this fiber is once again made local) with a connection B and a "coordinate field" x taking on values in the Minkowski space fiber.
More precisely, let the Minkowski space fiber be M. This is an affine space
. Using the abstract index notation
, let a, b, c,... refer to M and μ, ν, ... refer to the tangent bundle
. In any particular gauge, the value of xa at the point p is given by
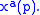
The covariant derivative
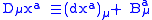
is defined with respect to the connection form
B. Here, d is the exterior derivative
of the ath component of x, which is a scalar field (so this isn't a pure abstract index notation). Under a gauge transformation by the translation field αa,

and

and so, the covariant derivative of xa is gauge invariant. This is identified with the tetrad eaμ (which is a one-form
which takes on values in the vector Minkowski space, not the affine Minkowski space, which is why it's gauge invariant). But what does this mean? xa is sort of like a coordinate function, giving an internal space value to each point p. The holonomy
associated with B specifies the displacement of a path according to the internal space.
A crude analogy: Think of M as the computer screen and the internal displacement as the position of the mouse pointer. Think of a curved mousepad as spacetime and the position of the mouse as the position. Keeping the orientation of the mouse fixed, if we move the mouse about the curved mousepad, the position of the mouse pointer (internal displacement) also changes and this change is path dependent; i.e., it doesn't only depend upon the initial and final position of the mouse. The change in the internal displacement as we move the mouse about a closed path on the mousepad is the torsion.
Another crude analogy: Think of a crystal
with line defects (edge dislocations and screw dislocations but not disclination
s). The parallel transport of a point of M along a path is given by counting the number of (up/down, forward/backwards and left/right) crystal bonds transversed. The Burgers vector
corresponds to the torsion. Disinclinations correspond to curvature, which is why they are left out.
The torsion,

is gauge invariant.
Of course, we can always choose the gauge where xa is zero everywhere (a problem though; M is an affine space and also a fiber and so, we have to define the "origin" on a point by point basis, but this can always be done arbitrarily) and this leads us back to the theory where the tetrad is fundamental.
Teleparallelism refers to any theory of gravitation based upon this framework. There is a particular choice of the action
which makes it exactly equivalent to general relativity, but there are also other choices of the action which aren't equivalent to GR. In some of these theories, there is no equivalence between inertial and gravitational masses.
Unlike GR, gravity is not due to the curvature of spacetime. It is due to the torsion.
There exits a close analogy of geometry
of spacetime with the structure of defects in crystal. Dislocations are represented by torsion, disclinations
by curvature.
These defects are not independent of each other.
A dislocation is equaivalent to a disclination-antidisclination pair, a disclination is equivalent to a string of dislocations.
This is the basic reason why Einstein's theory based purely on curvature can be rewritten as
a teleparallel theory based only on torsion.
There exists, moreover, infinitely many ways or rewriting
Einstein's theory, depending on how much of the curvature one wants to reexpress
in terms of torsion, the teleparallel theory being merely one specific version of these.
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
to unify electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and gravity. The idea is to use a geometry with a pseudo-Riemannian metric of signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(3,1), vanishing curvature
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, and non-vanishing torsion
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
, and to use tetrad
Cartan connection applications
The vierbein or tetrad theory much used in theoretical physics is a special case of the application of Cartan connection in four-dimensional manifolds. It applies to metrics of any signature. This section is an approach to tetrads, but written in general terms...
s, rather than the metric, as basic variables.
Nowadays, people study teleparallelism purely as a theory of gravity without trying to unify it with electromagnetism.
If this choice is made, then there is no longer any Lorentz gauge symmetry and the internal Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
fiber is now global. However, a translational gauge symmetry may be introduced thus: Instead of seeing tetrads as fundamental, we introduce a fundamental R4 translational gauge symmetry instead (which acts upon the internal Minkowski space fibers affine
Affine
Affine may refer to:*Affine cipher, a special case of the more general substitution cipher*Affine combination, a certain kind of constrained linear combination*Affine connection, a connection on the tangent bundle of a differentiable manifold...
ly so that this fiber is once again made local) with a connection B and a "coordinate field" x taking on values in the Minkowski space fiber.
More precisely, let the Minkowski space fiber be M. This is an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
. Using the abstract index notation
Abstract index notation
Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any fixed basis and, in particular, are non-numerical...
, let a, b, c,... refer to M and μ, ν, ... refer to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. In any particular gauge, the value of xa at the point p is given by
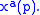
The covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
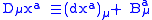
is defined with respect to the connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
B. Here, d is the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of the ath component of x, which is a scalar field (so this isn't a pure abstract index notation). Under a gauge transformation by the translation field αa,

and

and so, the covariant derivative of xa is gauge invariant. This is identified with the tetrad eaμ (which is a one-form
One-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
which takes on values in the vector Minkowski space, not the affine Minkowski space, which is why it's gauge invariant). But what does this mean? xa is sort of like a coordinate function, giving an internal space value to each point p. The holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
associated with B specifies the displacement of a path according to the internal space.
A crude analogy: Think of M as the computer screen and the internal displacement as the position of the mouse pointer. Think of a curved mousepad as spacetime and the position of the mouse as the position. Keeping the orientation of the mouse fixed, if we move the mouse about the curved mousepad, the position of the mouse pointer (internal displacement) also changes and this change is path dependent; i.e., it doesn't only depend upon the initial and final position of the mouse. The change in the internal displacement as we move the mouse about a closed path on the mousepad is the torsion.
Another crude analogy: Think of a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
with line defects (edge dislocations and screw dislocations but not disclination
Disclination
A disclination is a line defect in which rotational symmetry is violated. In analogy with dislocations in crystals, the term, disinclination, for liquid crystals first used by F. C. Frank and since then has been modified to its current usage, disclination.It is a defect in the orientation of...
s). The parallel transport of a point of M along a path is given by counting the number of (up/down, forward/backwards and left/right) crystal bonds transversed. The Burgers vector
Burgers vector
The Burgers vector, named after Dutch physicist Jan Burgers, is a vector, often denoted b, that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice....
corresponds to the torsion. Disinclinations correspond to curvature, which is why they are left out.
The torsion,

is gauge invariant.
Of course, we can always choose the gauge where xa is zero everywhere (a problem though; M is an affine space and also a fiber and so, we have to define the "origin" on a point by point basis, but this can always be done arbitrarily) and this leads us back to the theory where the tetrad is fundamental.
Teleparallelism refers to any theory of gravitation based upon this framework. There is a particular choice of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
which makes it exactly equivalent to general relativity, but there are also other choices of the action which aren't equivalent to GR. In some of these theories, there is no equivalence between inertial and gravitational masses.
Unlike GR, gravity is not due to the curvature of spacetime. It is due to the torsion.
There exits a close analogy of geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
of spacetime with the structure of defects in crystal. Dislocations are represented by torsion, disclinations
Disclination
A disclination is a line defect in which rotational symmetry is violated. In analogy with dislocations in crystals, the term, disinclination, for liquid crystals first used by F. C. Frank and since then has been modified to its current usage, disclination.It is a defect in the orientation of...
by curvature.
These defects are not independent of each other.
A dislocation is equaivalent to a disclination-antidisclination pair, a disclination is equivalent to a string of dislocations.
This is the basic reason why Einstein's theory based purely on curvature can be rewritten as
a teleparallel theory based only on torsion.
There exists, moreover, infinitely many ways or rewriting
Einstein's theory, depending on how much of the curvature one wants to reexpress
in terms of torsion, the teleparallel theory being merely one specific version of these.

