Szemerédi–Trotter theorem
Encyclopedia
The Szemerédi–Trotter theorem is a mathematical
result in the field of combinatorial geometry. It asserts that given n points and m lines in the plane,
the number of incidences
(i.e. the number of point-line pairs, such that the point lies on the line) is
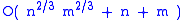, which is a bound that cannot be improved, except in terms of the implicit constants.
An equivalent formulation of the theorem is the following. Given n points and an integer k > 2, the number of lines
which pass through at least k of the points is
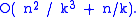
The original proof of Szemerédi and Trotter was somewhat complicated, using a combinatorial technique known as cell decomposition. Later, Székely discovered a much simpler proof using the crossing number inequality for graphs
. (See below.)
The Szemerédi–Trotter theorem has a number of consequences, including Beck's theorem
in incidence geometry.
the total number. Thus we may assume that every line contains at least three of the points.
If a line contains k points, then it will contain k−1 line segments which connect two of
the n points. In particular it will contain at least k/2 such line segments, since we have assumed k≥ 3.
Adding this up over all of the m lines, we see that the number of line segments obtained in this manner is at least
half of the total number of incidences. Thus if we let e be the number of such line segments, it will suffice to
show that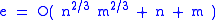
.
Now consider the graph
formed by using the n points as vertices, and the e line segments
as edges. Since all of the line segments lie on one of m lines, and any two lines intersect in at most one point, the crossing number
of this graph is at most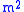
. Applying the crossing number inequality
we thus conclude that either e ≤ 7.5n, or that m2 ≥ e3 / 33.75n2. In either case e ≤ 3.24n2 / 3m2 / 3 + 7.5n and
we obtain the desired bound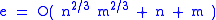
.
(e.g. if k ≤ C for some absolute constant C). Thus, we need only consider the case when k is large, say
k ≥ C.
Suppose that there are m lines that each contain at least k points. These lines generate at least mk incidences, and so by the first formulation of the Szemerédi–Trotter theorem, we have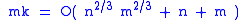
and so at least one of the statements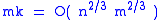
, 
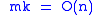, or
is true. The third possibility is ruled out since k was assumed to be large, so we are left
with the first two. But in either of these two cases, some elementary algebra will give the bound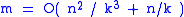
as desired.
Given a set of
points, 
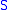, and the set of 
hyperplanes, 
, which are each spanned by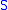 
, the number of incidences between 
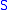and 
is bounded above by
Equivalently, the number of hyperplanes in
containing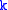 
or more points is bounded above by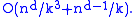
A construction due to Edelsbrunner shows this bound to be asymptotically optimal.
Solymosi and Tao
obtained near sharp upper bounds
for the number of incidences between points and algebraic varieties in higher dimensions. Their proof uses the Polynomial Ham Sandwhich Theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
result in the field of combinatorial geometry. It asserts that given n points and m lines in the plane,
the number of incidences
Incidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
(i.e. the number of point-line pairs, such that the point lies on the line) is
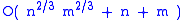, which is a bound that cannot be improved, except in terms of the implicit constants.An equivalent formulation of the theorem is the following. Given n points and an integer k > 2, the number of lines
which pass through at least k of the points is
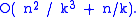
The original proof of Szemerédi and Trotter was somewhat complicated, using a combinatorial technique known as cell decomposition. Later, Székely discovered a much simpler proof using the crossing number inequality for graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
. (See below.)
The Szemerédi–Trotter theorem has a number of consequences, including Beck's theorem
Beck's theorem (geometry)
In the context of discrete geometry, Beck's theorem may refer to several different results, two of which are given below. Both appeared, alongside several other important theorems, in a well-known paper by József Beck. The two results described below primarily concern lower bounds on the number of...
in incidence geometry.
Proof of the first formulation
We may discard the lines which contain two or fewer of the points, as they can contribute at most 2m incidences tothe total number. Thus we may assume that every line contains at least three of the points.
If a line contains k points, then it will contain k−1 line segments which connect two of
the n points. In particular it will contain at least k/2 such line segments, since we have assumed k≥ 3.
Adding this up over all of the m lines, we see that the number of line segments obtained in this manner is at least
half of the total number of incidences. Thus if we let e be the number of such line segments, it will suffice to
show that
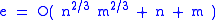.Now consider the graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
formed by using the n points as vertices, and the e line segments
as edges. Since all of the line segments lie on one of m lines, and any two lines intersect in at most one point, the crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
of this graph is at most
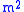. Applying the crossing number inequalitywe thus conclude that either e ≤ 7.5n, or that m2 ≥ e3 / 33.75n2. In either case e ≤ 3.24n2 / 3m2 / 3 + 7.5n and
we obtain the desired bound
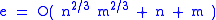.Proof of the second formulation
Since every pair of points can be connected by at most one line, there can be at most n(n − 1)/2 lines which can connect at k or more points, since k ≥ 2. This bound will prove the theorem when k is small(e.g. if k ≤ C for some absolute constant C). Thus, we need only consider the case when k is large, say
k ≥ C.
Suppose that there are m lines that each contain at least k points. These lines generate at least mk incidences, and so by the first formulation of the Szemerédi–Trotter theorem, we have
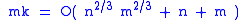
and so at least one of the statements
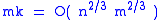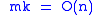, , or is true. The third possibility is ruled out since k was assumed to be large, so we are leftwith the first two. But in either of these two cases, some elementary algebra will give the bound
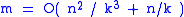as desired.Generalization to ℝd
One generalization of this result to arbitrary dimension, ℝd, was found by Agarwal and Aronov.Given a set of
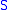points, , and the set of hyperplanes, , which are each spanned by 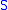, the number of incidences between 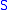and is bounded above byEquivalently, the number of hyperplanes in
containing 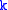or more points is bounded above by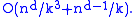A construction due to Edelsbrunner shows this bound to be asymptotically optimal.
Solymosi and Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
obtained near sharp upper bounds
for the number of incidences between points and algebraic varieties in higher dimensions. Their proof uses the Polynomial Ham Sandwhich Theorem.