Superreal number
Encyclopedia
In abstract algebra
, the superreal numbers are a class of extensions of the real numbers, introduced by H. Garth Dales and W. Hugh Woodin
as a generalization of the hyperreal number
s and primarily of interest in non-standard analysis
, model theory
, and the study of Banach algebra
s. The field
of superreals is itself a subfield of the surreal number
s.
Dales and Woodin's superreals are distinct from the super-real numbers of David O. Tall
, which are lexicographically ordered fractions of formal power series
over the reals.
, also called a T3.5 space, and C(X) is the algebra of continuous real-valued functions on X. Suppose P is a prime ideal
in C(X). Then the factor algebra A = C(X)/P is by definition an integral domain which is a real algebra and which can be seen to be totally ordered
. The field of fractions
F of A is a superreal field if F strictly contains the real numbers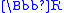
, so that F is not order isomorphic to 
.
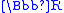If the prime ideal P is a maximal ideal, then F is a field of hyperreal number
s.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the superreal numbers are a class of extensions of the real numbers, introduced by H. Garth Dales and W. Hugh Woodin
W. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
as a generalization of the hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s and primarily of interest in non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
, model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, and the study of Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
s. The field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of superreals is itself a subfield of the surreal number
Surreal number
In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...
s.
Dales and Woodin's superreals are distinct from the super-real numbers of David O. Tall
David O. Tall
David Orme Tall is a mathematics education theorist at the University of Warwick. One of his most influential works is the joint paper with Vinner Concept image and concept definition.... The "concept image" is a notion in cognitive theory. It consists of all the cognitive structure in the...
, which are lexicographically ordered fractions of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
over the reals.
Formal Definition
Suppose X is a Tychonoff spaceTychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
, also called a T3.5 space, and C(X) is the algebra of continuous real-valued functions on X. Suppose P is a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
in C(X). Then the factor algebra A = C(X)/P is by definition an integral domain which is a real algebra and which can be seen to be totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
. The field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
F of A is a superreal field if F strictly contains the real numbers
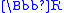, so that F is not order isomorphic to 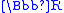.If the prime ideal P is a maximal ideal, then F is a field of hyperreal number
Hyperreal number
The system of hyperreal numbers represents a rigorous method of treating the infinite and infinitesimal quantities. The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form1 + 1 + \cdots + 1. \, Such a number is...
s.