
Subgradient method
Encyclopedia
Subgradient methods are iterative method
s for solving convex minimization problems. Originally developed by Naum Z. Shor
and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function. When the objective function is differentiable, subgradient methods for unconstrained problems use the same search direction as the method of steepest descent
.
Subgradient methods are slower than Newton's method when applied to minimize twice continuously differentiable convex functions. However, Newton's method fails to converge on problems that have non-differentiable kinks.
In recent years, some interior-point methods have been suggested for convex minimization problems, but subgradient projection methods and related bundle methods of descent remain competitive. For convex minimization problems with very large number of dimensions, subgradient-projection methods are suitable, because they require little storage.
Subgradient projection methods are often applied to large-scale problems with decomposition techniques. Such decomposition methods often allow a simple distributed method for a problem.
 be a convex function
be a convex function
with domain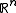 . A classical subgradient method iterates
. A classical subgradient method iterates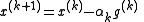
where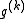 denotes a subgradient of
denotes a subgradient of  at
at 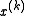 . If
. If  is differentiable, then its only subgradient is the gradient vector
is differentiable, then its only subgradient is the gradient vector 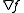 itself.
itself.
It may happen that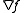 is not a descent direction for
is not a descent direction for 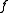 at
at 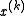 . We therefore maintain a list
. We therefore maintain a list 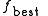 that keeps track of the lowest objective function value found so far, i.e.
that keeps track of the lowest objective function value found so far, i.e.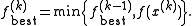
s are known:
For all five rules, the step-sizes are determined "off-line", before the method is iterated; the step-sizes do not depend on preceding iterations. This "off-line" property of subgradient methods differs from the "on-line" step-size rules used for descent methods for differentiable functions: Many methods for minimizing differentiable functions satisfy Wolfe's sufficient conditions for convergence, where step-sizes typically depend on the current point and the current search-direction.
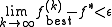 by a result of Shor
by a result of Shor
.
These classical subgradient methods have poor performance and are no longer recommended for general use.
and Phil. Wolfe proposed "bundle methods" of descent for problems of convex minimization. Contemporary bundle-methods often use "level
control" rules for choosing step-sizes, developing techniques from the "subgradient-projection" method of Boris T. Polyak (1969). However, there are problems on which bundle methods offer little advantage over subgradient-projection methods.
where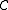 is a convex set. The projected subgradient method uses the iteration
is a convex set. The projected subgradient method uses the iteration
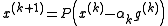
where is projection on
is projection on 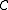 and
and 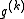 is any subgradient of
is any subgradient of 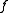 at
at 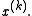
where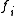 are convex. The algorithm takes the same form as the unconstrained case
are convex. The algorithm takes the same form as the unconstrained case
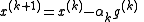
where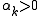 is a step size, and
is a step size, and 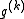 is a subgradient of the objective or one of the constraint functions at
is a subgradient of the objective or one of the constraint functions at 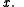 Take
Take
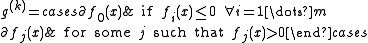
where denotes the subdifferential of
denotes the subdifferential of 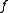 . If the current point is feasible, the algorithm uses an objective subgradient; if the current point is infeasible, the algorithm chooses a subgradient of any violated constraint.
. If the current point is feasible, the algorithm uses an objective subgradient; if the current point is infeasible, the algorithm chooses a subgradient of any violated constraint.
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s for solving convex minimization problems. Originally developed by Naum Z. Shor
Naum Z. Shor
Naum Zuselevich Shor was a Soviet and Ukrainian Jewish mathematician specializing in optimization.He made significant contributions to nonlinear and stochastic programming, numerical techniques for non-smooth optimization, discrete optimization problems, matrix optimization, dual quadratic bounds...
and others in the 1960s and 1970s, subgradient methods are convergent when applied even to a non-differentiable objective function. When the objective function is differentiable, subgradient methods for unconstrained problems use the same search direction as the method of steepest descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
.
Subgradient methods are slower than Newton's method when applied to minimize twice continuously differentiable convex functions. However, Newton's method fails to converge on problems that have non-differentiable kinks.
In recent years, some interior-point methods have been suggested for convex minimization problems, but subgradient projection methods and related bundle methods of descent remain competitive. For convex minimization problems with very large number of dimensions, subgradient-projection methods are suitable, because they require little storage.
Subgradient projection methods are often applied to large-scale problems with decomposition techniques. Such decomposition methods often allow a simple distributed method for a problem.
Classical subgradient rules
Let be a convex function
be a convex functionConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
with domain
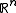 . A classical subgradient method iterates
. A classical subgradient method iterates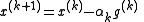
where
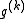 denotes a subgradient of
denotes a subgradient of  at
at 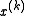 . If
. If  is differentiable, then its only subgradient is the gradient vector
is differentiable, then its only subgradient is the gradient vector 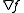 itself.
itself.It may happen that
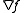 is not a descent direction for
is not a descent direction for 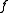 at
at 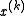 . We therefore maintain a list
. We therefore maintain a list 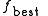 that keeps track of the lowest objective function value found so far, i.e.
that keeps track of the lowest objective function value found so far, i.e.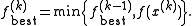
Step size rules
Many different types of step-size rules are used by subgradient methods. This article notes five classical step-size rules for which convergence proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
s are known:
- Constant step size,
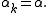
- Constant step length,
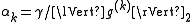 , which gives
, which gives 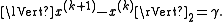
- Square summable but not summable step size, i.e. any step sizes satisfying
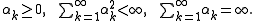
- Nonsummable diminishing, i.e. any step sizes satisfying
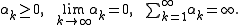
- Nonsummable diminishing step lengths, i.e.
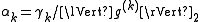 , where
, where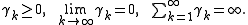
For all five rules, the step-sizes are determined "off-line", before the method is iterated; the step-sizes do not depend on preceding iterations. This "off-line" property of subgradient methods differs from the "on-line" step-size rules used for descent methods for differentiable functions: Many methods for minimizing differentiable functions satisfy Wolfe's sufficient conditions for convergence, where step-sizes typically depend on the current point and the current search-direction.
Convergence results
For constant step-length and scaled subgradients having Euclidean norm equal to one, the subgradient method converges to an arbitrarily close approximation to the minimum value, that is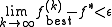 by a result of Shor
by a result of ShorNaum Z. Shor
Naum Zuselevich Shor was a Soviet and Ukrainian Jewish mathematician specializing in optimization.He made significant contributions to nonlinear and stochastic programming, numerical techniques for non-smooth optimization, discrete optimization problems, matrix optimization, dual quadratic bounds...
.
These classical subgradient methods have poor performance and are no longer recommended for general use.
Subgradient-projection & bundle methods
During the 1970s, Claude LemaréchalClaude Lemaréchal
Claude Lemaréchal is a French applied mathematician.In mathematical optimization, Claude Lemaréchal is known for his work in numerical methods for nonlinear optimization, especially for problems with nondifferentiable kinks. Lemaréchal and Phil...
and Phil. Wolfe proposed "bundle methods" of descent for problems of convex minimization. Contemporary bundle-methods often use "level
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
control" rules for choosing step-sizes, developing techniques from the "subgradient-projection" method of Boris T. Polyak (1969). However, there are problems on which bundle methods offer little advantage over subgradient-projection methods.
Projected subgradient
One extension of the subgradient method is the projected subgradient method, which solves the constrained optimization problem- minimize
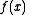 subject to
subject to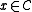
where
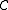 is a convex set. The projected subgradient method uses the iteration
is a convex set. The projected subgradient method uses the iteration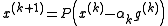
where
 is projection on
is projection on 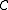 and
and 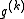 is any subgradient of
is any subgradient of 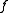 at
at 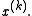
General constraints
The subgradient method can be extended to solve the inequality constrained problem- minimize
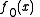 subject to
subject to
where
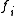 are convex. The algorithm takes the same form as the unconstrained case
are convex. The algorithm takes the same form as the unconstrained case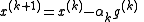
where
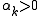 is a step size, and
is a step size, and 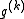 is a subgradient of the objective or one of the constraint functions at
is a subgradient of the objective or one of the constraint functions at 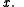 Take
Take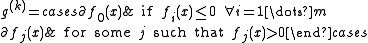
where
 denotes the subdifferential of
denotes the subdifferential of 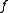 . If the current point is feasible, the algorithm uses an objective subgradient; if the current point is infeasible, the algorithm chooses a subgradient of any violated constraint.
. If the current point is feasible, the algorithm uses an objective subgradient; if the current point is infeasible, the algorithm chooses a subgradient of any violated constraint.
