Stokes' law
Encyclopedia

George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
objects with very small Reynolds numbers (e.g., very small particles) in a continuous viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
. Stokes' law is derived by solving the Stokes flow limit for small Reynolds numbers of the generally unsolvable Navier–Stokes equations:

where:
- Fd is the frictional force acting on the interface between the fluid and the particle (in N),
- μ is the dynamic viscosity (N s/m2),
- R is the radius of the spherical object (in m), and
- vs is the particle's settling velocity (in m/s).
If the particles are falling in the viscous fluid by their own weight due to gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
, then a terminal velocity
Terminal velocity
In fluid dynamics an object is moving at its terminal velocity if its speed is constant due to the restraining force exerted by the fluid through which it is moving....
, also known as the settling velocity, is reached when this frictional force combined with the buoyant force exactly balance the gravitational force. The resulting settling velocity (or terminal velocity) is given by:
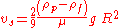
where:
- vs is the particles' settling velocity (m/s) (vertically downwards if ρp > ρf, upwards if ρp < ρf ),
- g is the gravitational accelerationEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
(m/s2), - ρp is the mass density of the particles (kg/m3), and
- ρf is the mass density of the fluid (kg/m3).
Note that for molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s Stokes' law is used to define their Stokes radius
Stokes radius
The Stokes radius, Stokes-Einstein radius, or hydrodynamic radius RH, named after George Gabriel Stokes, is not the effective radius of a hydrated molecule in solution as often mentioned. Rather it is the radius of a hard sphere that diffuses at the same rate as the molecule. The behavior of this...
.
The CGS unit of kinematic viscosity was named "stokes" after his work.
Applications
Stokes's law is the basis of the falling-sphere viscometerViscometer
A viscometer is an instrument used to measure the viscosity of a fluid. For liquids with viscosities which vary with flow conditions, an instrument called a rheometer is used...
, in which the fluid is stationary in a vertical glass tube. A sphere of known size and density is allowed to descend through the liquid. If correctly selected, it reaches terminal velocity, which can be measured by the time it takes to pass two marks on the tube. Electronic sensing can be used for opaque fluids. Knowing the terminal velocity, the size and density of the sphere, and the density of the liquid, Stokes' law can be used to calculate the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
of the fluid. A series of steel ball bearings of different diameters are normally used in the classic experiment to improve the accuracy of the calculation. The school experiment uses glycerine or golden syrup
Golden syrup
Golden syrup is a pale treacle. It is a thick, amber-colored form of inverted sugar syrup, made in the process of refining sugar cane juice into sugar, or by treatment of a sugar solution with acid. It is used in a variety of baking recipes and desserts. It has an appearance similar to honey, and...
as the fluid, and the technique is used industrially to check the viscosity of fluids used in processes. Several school experiments often involve varying the temperature and/or concentration of the substances used in order to demonstrate the effects this has on the viscosity. Industrial methods include many different oil
Oil
An oil is any substance that is liquid at ambient temperatures and does not mix with water but may mix with other oils and organic solvents. This general definition includes vegetable oils, volatile essential oils, petrochemical oils, and synthetic oils....
s, and polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
liquids such as solutions.
The importance of Stokes' law is illustrated by the fact that it played a critical role in the research leading to at least 3 Nobel Prizes.
Stokes' law is important to understanding the swimming of microorganism
Microorganism
A microorganism or microbe is a microscopic organism that comprises either a single cell , cell clusters, or no cell at all...
s and sperm
Sperm
The term sperm is derived from the Greek word sperma and refers to the male reproductive cells. In the types of sexual reproduction known as anisogamy and oogamy, there is a marked difference in the size of the gametes with the smaller one being termed the "male" or sperm cell...
; also, the sedimentation
Sedimentation
Sedimentation is the tendency for particles in suspension to settle out of the fluid in which they are entrained, and come to rest against a barrier. This is due to their motion through the fluid in response to the forces acting on them: these forces can be due to gravity, centrifugal acceleration...
, under the force of gravity, of small particles and organisms, in water.
In air, the same theory can be used to explain why small water droplets (or ice crystals) can remain suspended in air (as clouds) until they grow to a critical size and start falling as rain (or snow and hail). Similar use of the equation can be made in the settlement of fine particles in water or other fluids.
Steady Stokes flow
In Stokes flow, at very low Reynolds number, the convective accelerationAdvection
Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
terms in the Navier–Stokes equations are neglected. Then the flow equations become, for an incompressible
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
steady flow:
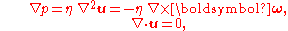
where:
- p is the fluid pressure (in Pa),
- u is the flow velocityFlow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
(in m/s), and - ω is the vorticity (in s-1), defined as
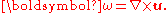
By using some vector calculus identities, these equations can be shown to result in Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
s for the pressure and each of the components of the vorticity vector:
 and
and 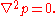
Additional forces like those by gravity and buoyancy have not been taken into account, but can easily be added since the above equations are linear, so linear superposition of solutions and associated forces can be applied.
Flow around a sphere
For the case of a sphere in a uniform far field flow, it is advantageous to use a cylindrical coordinate systemCylindrical coordinate system
A cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
( r , φ , z ). The z–axis is through the centre of the sphere and aligned with the mean flow direction, while r is the radius as measured perpendicular to the z–axis. The origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
is at the sphere centre. Because the flow is axisymmetric around the z–axis, it is independent of the azimuth φ.
In this cylindrical coordinate system, the incompressible flow can be described with a Stokes stream function
Stokes stream function
In fluid dynamics, the Stokes stream function is used to describe the streamlines and flow velocity in a three-dimensional incompressible flow with axisymmetry. A surface with a constant value of the Stokes stream function encloses a streamtube, everywhere tangential to the flow velocity vectors...
ψ, depending on r and z:

with v and w the flow velocity components in the r and z direction, respectively. The azimuthal velocity component in the φ–direction is equal to zero, in this axisymmetric case. The volume flux, through a tube bounded by a surface of some constant value ψ, is equal to 2π ψ and is constant.
For this case of an axisymmetric flow, the only non-zero of the vorticity vector ω is the azimuthal φ–component ωφ
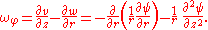
The Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, applied to the vorticity ωφ, becomes in this cylindrical coordinate system with axisymmetry:

From the previous two equations, and with the appropriate boundary conditions, for a far-field uniform-flow velocity V in the z–direction and a sphere of radius R, the solution is found to be
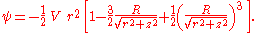
The viscous force per unit area σ, exerted by the flow on the surface on the sphere, is in the z–direction everywhere. More strikingly, it has also the same value everywhere on the sphere:
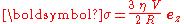
with ez the unit vector in the z–direction. For other shapes than spherical, σ is not constant along the body surface. Integration of the viscous force per unit area σ over the sphere surface gives the frictional force Fd according to Stokes' law.
Terminal velocity and settling time
At terminal velocity – or settling velocity – the frictional force Fd on the sphere is balanced by the excess force Fg due to the difference of the weightWeight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
of the sphere and its buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
, both caused by gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
:

with ρp and ρf the mass density of the sphere and the fluid, respectively, and g the gravitational acceleration
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
. Demanding force balance: Fd = Fg and solving for the velocity V gives the terminal velocity Vs. If terminal velocity is reached relatively quickly, an average settling time can be calculated by dividing the height the particle will fall by its terminal velocity.
See also
- Einstein relation (kinetic theory)Einstein relation (kinetic theory)In physics the Einstein relation is a previously unexpected connection revealed independently by Albert Einstein in 1905 and by Marian Smoluchowski in their papers on Brownian motion...
- Scientific laws named after peopleScientific laws named after peopleThis is a list of scientific laws named after people . For other lists of eponyms, see eponym.-See also:* Eponym* Fields of science...
- Drag (physics)Drag (physics)In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
- Viscometry
- Equivalent spherical diameterEquivalent spherical diameterIn science, the equivalent spherical diameter of an irregularly-shaped object is the diameter of a sphere of equivalent volume.According to the IUPAC definition, the equivalent diameter of a non-spherical particle is equal to a diameter of a spherical particle that exhibits identical property to...

