
Stochastic computing
Encyclopedia
Stochastic computing is a collection of techniques that represent continuous values by streams of random bits. Complex computations can then be computed by simple bit-wise operations on the streams.
Despite the similarity in their names, stochastic computing is distinct from the study of randomized algorithm
s.
 is given, and we wish to compute
is given, and we wish to compute  . Stochastic computing performs this operation using probability instead of arithmetic.
. Stochastic computing performs this operation using probability instead of arithmetic.
Specifically, suppose that there are two random, independent bit streams (i.e. Bernoulli process
es), where the probability of a one in the first stream is , and the probability in the second stream is
, and the probability in the second stream is  . We can take the logical AND of the two streams.
. We can take the logical AND of the two streams.
The probability of a one in the output stream is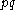 . By observing enough output bits and measuring the frequency of ones, it is possible to estimate
. By observing enough output bits and measuring the frequency of ones, it is possible to estimate 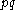 to arbitrary accuracy.
to arbitrary accuracy.
The operation above converts a fairly complicated computation (multiplication of and
and  ) into a series of very simple operations (evaluation of
) into a series of very simple operations (evaluation of  ) on random bits.
) on random bits.
More generally speaking, stochastic computing represents numbers as streams of random bits and reconstructs numbers by calculating frequencies. The computations are performed on the streams and translate complicated operations on and
and  into simple operations on their stream representations. (Because of the method of reconstruction, devices that perform these operations are sometimes called stochastic averaging processors.) In modern terms, stochastic computing can be viewed as an interpretation of calculations in probabilistic terms, which are then evaluated with a Gibbs sampler
into simple operations on their stream representations. (Because of the method of reconstruction, devices that perform these operations are sometimes called stochastic averaging processors.) In modern terms, stochastic computing can be viewed as an interpretation of calculations in probabilistic terms, which are then evaluated with a Gibbs sampler
.
in 1953. However, the
theory could not be fully developed until advances in computing of the 1960s,
mostly through a series of simultaneous and parallel efforts in the US
and the UK.
By the late 1960s, attention turned to the design of
special-purpose hardware to perform stochastic computation. A host
of these machines were constructed between 1969 and 1974; RASCEL
is pictured in this article.
Despite the intense interest in the 1960s and 1970s, stochastic
computing ultimately failed to compete with more traditional digital
logic, for reasons outlined below. The first (and last)
International Symposium on Stochastic Computing
took place in 1978; active research in the area dwindled over the next
few years.
Although stochastic computing declined as a general method of
computing, it has shown promise in several applications. Research has
traditionally focused on certain tasks in machine learning and
control.
More recently, interest has turned towards stochastic
decoding, which applies stochastic computing to the decoding of error
correcting codes.
solving certain problems. To understand when it remains relevant, it is useful to
compare stochastic computing with more traditional methods of digital computing.
two numbers each with bits of precision.
bits of precision.
Using the typical long
multiplication method, we need to perform
 operations. With stochastic computing, we can
operations. With stochastic computing, we can
AND together any number of bits and the expected value will always
be correct. (However, with a small number of samples the variance will
render the actual result highly inaccurate).
Moreover, the underlying operations in a digital multiplier are
full adders, whereas a stochastic
computer only requires an AND gate
. Additionally,
a digital multiplier would naively require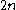 input wires,
input wires,
whereas a stochastic multiplier would only require 2 input wires.
(If the digital multiplier serialized its output, however, it would also
require only 2 input wires.)
Additionally, stochastic computing is robust against noise; if a few
bits in a stream are flipped, those errors will have no significant impact
on the solution.
Finally, stochastic computing provides an estimate of the solution
that grows more accurate as we extend the bit stream. In particular,
it provides a rough estimate very rapidly. In some
iterative systems these partial solutions can provide faster feedback
than through traditional computing methods, leading to faster
convergence.
a random bit stream and try to reconstruct the underlying value, the effective precision
can be measured by the variance of our sample. In the example above, the digital multiplier
computes a number to bits of accuracy, so the
bits of accuracy, so the
precision is . If we are using a random bit
. If we are using a random bit
stream to estimate a number and want the standard deviation of our
estimate of the solution to be at least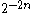 , we
, we
would need samples. This represents an
samples. This represents an
exponential increase in work.
Second, stochastic computing requires a method of generating random
biased bit streams. In practice, these streams are generated with
pseudo-random number generators. Unfortunately, generating
(pseudo-)random bits is fairly costly (compared to the expense of,
e.g., a full adder). Therefore, the gate-level advantage of
stochastic computing is typically lost.
Third, the analysis of stochastic computing assumes that the bit
streams are independent (uncorrelated). If this assumption does not
hold, stochastic computing can fail dramatically. For instance, if we
try to compute by multiplying a bit stream for
by multiplying a bit stream for
 by itself, the process fails: since
by itself, the process fails: since  , the stochastic computation would yield
, the stochastic computation would yield  , which is not generally true (unless
, which is not generally true (unless  0 or 1).
0 or 1).
In systems with feedback, the problem of decorrelation can manifest in
more complicated ways. Systems of stochastic processors are prone to
latching, where feedback between different components can achieve
a deadlocked state.
A great deal of effort must be spent decorrelating the system to
attempt to remediate latching.
Fourth, although some digital functions have very simple stochastic
counterparts (such as the translation between multiplication and the
AND gate), many do not. Trying to express these functions stochastically
may cause various pathologies. For instance, stochastic decoding requires
the computation of the function .
.
There is no single bit operation that can compute this function; the usual solution
involves producing correlated output bits, which, as we have seen above, can cause
a host of problems. Still other functions (such as the
averaging operator ) require
) require
stream decimation. Since decimation discards information, it leads to the problem
of attenuation.
as a method of general computation, there are certain applications
that highlight its strengths. One notable case occurs in the
decoding of certain error correcting codes.
In developments unrelated to stochastic computing, highly effective
methods of decoding LDPC codes
using
the belief propagation
algorithm were
developed. Belief propagation in this context involves iteratively
reestimating certain parameters using two basic operations
(essentially, a probabilistic XOR operation and an averaging
operation).
In 2003, researchers realized that these two operations could be
modeled very simply with stochastic computing.
Moreover, since the
belief propagation algorithm is iterative, stochastic computing provides partial
solutions that may lead to faster convergence.
Hardware implementations of stochastic decoders have been built on FPGAs
.
The proponents of these methods argue that the performance of stochastic decoding is
competitive with digital alternatives.
paradigm. Further information can be found in the referenced book by
Mars and Poppelbaum.
Bundle Processing involves sending a fixed number of
bits instead of a stream. One of the advantages of this approach is
that the precision is improved. To see why, suppose we transmit
 bits. In regular stochastic computing, we can
bits. In regular stochastic computing, we can
represent a precision of roughly different
different
values, because of the variance of the estimate. In bundle
processing, we can represent a precision of .
.
However, bundle processing retains the same robustness to error of
regular stochastic processing.
Ergodic Processing involves sending a stream of bundles, which
captures the benefits of regular stochastic and bundle processing.
Burst Processing encodes a number by a higher base increasing
stream. For instance, we would encode 4.3 with ten decimal digits as
since the average value of the preceding stream is 4.3. This
representation offers various advantages: there is no randomization
since the numbers appear in increasing order,
so the PRNG issues are avoided, but many of the advantages of
stochastic computing are retained (such as partial estimates of the
solution). Additionally, it retains the linear precision of bundle
and ergodic processing.
Despite the similarity in their names, stochastic computing is distinct from the study of randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s.
Motivation and a simple example
Suppose that is given, and we wish to compute
is given, and we wish to compute  . Stochastic computing performs this operation using probability instead of arithmetic.
. Stochastic computing performs this operation using probability instead of arithmetic.Specifically, suppose that there are two random, independent bit streams (i.e. Bernoulli process
Bernoulli process
In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
es), where the probability of a one in the first stream is
 , and the probability in the second stream is
, and the probability in the second stream is  . We can take the logical AND of the two streams.
. We can take the logical AND of the two streams. 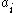 |
1 | 0 | 1 | 1 | 0 | 1 | ... |
|---|---|---|---|---|---|---|---|
 |
1 | 1 | 0 | 1 | 1 | 0 | ... |
 |
1 | 0 | 0 | 1 | 0 | 0 | ... |
The probability of a one in the output stream is
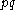 . By observing enough output bits and measuring the frequency of ones, it is possible to estimate
. By observing enough output bits and measuring the frequency of ones, it is possible to estimate 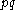 to arbitrary accuracy.
to arbitrary accuracy.The operation above converts a fairly complicated computation (multiplication of
 and
and  ) into a series of very simple operations (evaluation of
) into a series of very simple operations (evaluation of  ) on random bits.
) on random bits.More generally speaking, stochastic computing represents numbers as streams of random bits and reconstructs numbers by calculating frequencies. The computations are performed on the streams and translate complicated operations on
 and
and  into simple operations on their stream representations. (Because of the method of reconstruction, devices that perform these operations are sometimes called stochastic averaging processors.) In modern terms, stochastic computing can be viewed as an interpretation of calculations in probabilistic terms, which are then evaluated with a Gibbs sampler
into simple operations on their stream representations. (Because of the method of reconstruction, devices that perform these operations are sometimes called stochastic averaging processors.) In modern terms, stochastic computing can be viewed as an interpretation of calculations in probabilistic terms, which are then evaluated with a Gibbs samplerGibbs sampling
In statistics and in statistical physics, Gibbs sampling or a Gibbs sampler is an algorithm to generate a sequence of samples from the joint probability distribution of two or more random variables...
.
History
Stochastic computing was first introduced in a pioneering paper by John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in 1953. However, the
theory could not be fully developed until advances in computing of the 1960s,
mostly through a series of simultaneous and parallel efforts in the US
and the UK.
By the late 1960s, attention turned to the design of
special-purpose hardware to perform stochastic computation. A host
of these machines were constructed between 1969 and 1974; RASCEL
is pictured in this article.
Despite the intense interest in the 1960s and 1970s, stochastic
computing ultimately failed to compete with more traditional digital
logic, for reasons outlined below. The first (and last)
International Symposium on Stochastic Computing
took place in 1978; active research in the area dwindled over the next
few years.
Although stochastic computing declined as a general method of
computing, it has shown promise in several applications. Research has
traditionally focused on certain tasks in machine learning and
control.
More recently, interest has turned towards stochastic
decoding, which applies stochastic computing to the decoding of error
correcting codes.
Strengths and weaknesses
Although stochastic computing was a historical failure, it may still remain relevant forsolving certain problems. To understand when it remains relevant, it is useful to
compare stochastic computing with more traditional methods of digital computing.
Strengths
Suppose we wish to multiplytwo numbers each with
 bits of precision.
bits of precision.Using the typical long
multiplication method, we need to perform
 operations. With stochastic computing, we can
operations. With stochastic computing, we canAND together any number of bits and the expected value will always
be correct. (However, with a small number of samples the variance will
render the actual result highly inaccurate).
Moreover, the underlying operations in a digital multiplier are
full adders, whereas a stochastic
computer only requires an AND gate
AND gate
The AND gate is a basic digital logic gate that implements logical conjunction - it behaves according to the truth table to the right. A HIGH output results only if both the inputs to the AND gate are HIGH . If neither or only one input to the AND gate is HIGH, a LOW output results...
. Additionally,
a digital multiplier would naively require
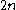 input wires,
input wires,whereas a stochastic multiplier would only require 2 input wires.
(If the digital multiplier serialized its output, however, it would also
require only 2 input wires.)
Additionally, stochastic computing is robust against noise; if a few
bits in a stream are flipped, those errors will have no significant impact
on the solution.
Finally, stochastic computing provides an estimate of the solution
that grows more accurate as we extend the bit stream. In particular,
it provides a rough estimate very rapidly. In some
iterative systems these partial solutions can provide faster feedback
than through traditional computing methods, leading to faster
convergence.
Weaknesses
Stochastic computing is, by its very nature, random. When we examinea random bit stream and try to reconstruct the underlying value, the effective precision
can be measured by the variance of our sample. In the example above, the digital multiplier
computes a number to
 bits of accuracy, so the
bits of accuracy, so theprecision is
 . If we are using a random bit
. If we are using a random bitstream to estimate a number and want the standard deviation of our
estimate of the solution to be at least
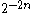 , we
, wewould need
 samples. This represents an
samples. This represents anexponential increase in work.
Second, stochastic computing requires a method of generating random
biased bit streams. In practice, these streams are generated with
pseudo-random number generators. Unfortunately, generating
(pseudo-)random bits is fairly costly (compared to the expense of,
e.g., a full adder). Therefore, the gate-level advantage of
stochastic computing is typically lost.
Third, the analysis of stochastic computing assumes that the bit
streams are independent (uncorrelated). If this assumption does not
hold, stochastic computing can fail dramatically. For instance, if we
try to compute
 by multiplying a bit stream for
by multiplying a bit stream for by itself, the process fails: since
by itself, the process fails: since  , the stochastic computation would yield
, the stochastic computation would yield  , which is not generally true (unless
, which is not generally true (unless  0 or 1).
0 or 1).In systems with feedback, the problem of decorrelation can manifest in
more complicated ways. Systems of stochastic processors are prone to
latching, where feedback between different components can achieve
a deadlocked state.
A great deal of effort must be spent decorrelating the system to
attempt to remediate latching.
Fourth, although some digital functions have very simple stochastic
counterparts (such as the translation between multiplication and the
AND gate), many do not. Trying to express these functions stochastically
may cause various pathologies. For instance, stochastic decoding requires
the computation of the function
 .
.There is no single bit operation that can compute this function; the usual solution
involves producing correlated output bits, which, as we have seen above, can cause
a host of problems. Still other functions (such as the
averaging operator
 ) require
) requirestream decimation. Since decimation discards information, it leads to the problem
of attenuation.
Stochastic decoding
Although stochastic computing has a number of defects when consideredas a method of general computation, there are certain applications
that highlight its strengths. One notable case occurs in the
decoding of certain error correcting codes.
In developments unrelated to stochastic computing, highly effective
methods of decoding LDPC codes
Low-density parity-check code
In information theory, a low-density parity-check code is a linear error correcting code, a method of transmitting a message over a noisy transmission channel, and is constructed using a sparse bipartite graph...
using
the belief propagation
Belief propagation
Belief propagation is a message passing algorithm for performing inference on graphical models, such as Bayesian networks and Markov random fields. It calculates the marginal distribution for each unobserved node, conditional on any observed nodes...
algorithm were
developed. Belief propagation in this context involves iteratively
reestimating certain parameters using two basic operations
(essentially, a probabilistic XOR operation and an averaging
operation).
In 2003, researchers realized that these two operations could be
modeled very simply with stochastic computing.
Moreover, since the
belief propagation algorithm is iterative, stochastic computing provides partial
solutions that may lead to faster convergence.
Hardware implementations of stochastic decoders have been built on FPGAs
Field-programmable gate array
A field-programmable gate array is an integrated circuit designed to be configured by the customer or designer after manufacturing—hence "field-programmable"...
.
The proponents of these methods argue that the performance of stochastic decoding is
competitive with digital alternatives.
Variants of stochastic computing
There are a number of variants of the basic stochastic computingparadigm. Further information can be found in the referenced book by
Mars and Poppelbaum.
Bundle Processing involves sending a fixed number of
bits instead of a stream. One of the advantages of this approach is
that the precision is improved. To see why, suppose we transmit
 bits. In regular stochastic computing, we can
bits. In regular stochastic computing, we canrepresent a precision of roughly
 different
differentvalues, because of the variance of the estimate. In bundle
processing, we can represent a precision of
 .
.However, bundle processing retains the same robustness to error of
regular stochastic processing.
Ergodic Processing involves sending a stream of bundles, which
captures the benefits of regular stochastic and bundle processing.
Burst Processing encodes a number by a higher base increasing
stream. For instance, we would encode 4.3 with ten decimal digits as
-
-
- 4444444555
-
since the average value of the preceding stream is 4.3. This
representation offers various advantages: there is no randomization
since the numbers appear in increasing order,
so the PRNG issues are avoided, but many of the advantages of
stochastic computing are retained (such as partial estimates of the
solution). Additionally, it retains the linear precision of bundle
and ergodic processing.

