State function
Encyclopedia
In thermodynamics
, a state function, function of state, state quantity, or state variable is a property
of a system that depends only on the current state of the system
, not on the way in which the system acquired that state (independent of path). A state function describes the equilibrium state of a system
. For example, internal energy
, enthalpy
, and entropy
are state quantities because they describe quantitatively an equilibrium state of a thermodynamic system, irrespective of how the system arrived in that state. In contrast, mechanical work
and heat
are process quantities
because their values depend on the specific transition (or path) between two equilibrium states.
The opposite of a state function is a path function.
, William Rankine
, Peter Tait
, William Thomson
, and it is clear that by the 1870s the term had acquired a use of its own. In 1873, for example, Willard Gibbs, in his paper “Graphical Methods in the Thermodynamics of Fluids”, states: “The quantities V, B, T, U, and S are determined when the state of the body is given, and it may be permitted to call them functions of the state of the body.”
, volume, pressure
) which are not necessarily independent. The number of parameters needed to describe the system is the dimension of the state space
of the system (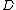
). For example, a monatomic gas
with a fixed number of particles is a simple case of a two-dimensional system (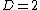
). In this example, any system is uniquely specified by two parameters, such as pressure and volume, or perhaps pressure and temperature. These choices are equivalent. They are simply different coordinate systems in the two-dimensional thermodynamic state space. An analogous statement holds for higher dimensional spaces, as described by the state postulate
.
When a system changes state continuously, it traces out a "path" in the state space. The path can be specified by noting the values of the state parameters as the system traces out the path, perhaps as a function of time, or some other external variable. For example, we might have the pressure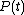
and the volume 
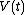as functions of time from time 
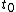to 
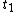. This will specify a path in our two dimensional state space example. We can now form all sorts of functions of time which we may integrate over the path. For example if we wish to calculate the work done by the system from time 
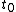to time 
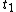we calculate
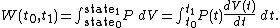
It is clear that in order to calculate the work W in the above integral, we will have to know the functions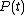
and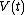 
at each time 
, over the entire path. A state function is a function of the parameters of the system which only depends upon the parameters' values at the endpoints of the path. For example, suppose we wish to calculate the work plus the integral of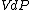 
over the path. We would have:
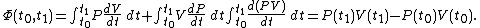
It can be seen that the integrand can be expressed as the exact differential
of the function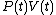
and that therefore, the integral can be expressed as the difference in the value of 
at the end points of the integration. The product 
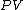is therefore a state function of the system.
By way of notation, we will specify the use of d to denote an exact differential. In other words, the integral of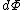
will be equal to 
. The symbol δ will be reserved for an inexact differential, which cannot be integrated without full knowledge of the path. For example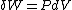 
will be used to denote an infinitesimal increment of work.
It is best to think of state functions as quantities or properties of a thermodynamic system, while non-state functions represent a process during which the state functions change. For example, the state function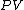
is proportional to the internal energy of an ideal gas, but the work 
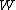is the amount of energy transferred as the system performs work. Internal energy is identifiable, it is a particular form of energy. Work is the amount of energy that has changed its form or location.
:
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, a state function, function of state, state quantity, or state variable is a property
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
of a system that depends only on the current state of the system
Thermodynamic state
A thermodynamic state is a set of values of properties of a thermodynamic system that must be specified to reproduce the system. The individual parameters are known as state variables, state parameters or thermodynamic variables. Once a sufficient set of thermodynamic variables have been...
, not on the way in which the system acquired that state (independent of path). A state function describes the equilibrium state of a system
System
System is a set of interacting or interdependent components forming an integrated whole....
. For example, internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
, enthalpy
Enthalpy
Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
, and entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
are state quantities because they describe quantitatively an equilibrium state of a thermodynamic system, irrespective of how the system arrived in that state. In contrast, mechanical work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
and heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
are process quantities
Process function
A process function, process quantity, or a path function is a physical quantity that describes the transition of a system from an equilibrium state to another equilibrium state. As an example, mechanical work and heat are process quantities because they describe quantitatively the transition...
because their values depend on the specific transition (or path) between two equilibrium states.
The opposite of a state function is a path function.
History
It is likely that the term “functions of state” was used in a loose sense during the 1850s and 60s by those such as Rudolf ClausiusRudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
, William Rankine
William John Macquorn Rankine
William John Macquorn Rankine was a Scottish civil engineer, physicist and mathematician. He was a founding contributor, with Rudolf Clausius and William Thomson , to the science of thermodynamics....
, Peter Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
, William Thomson
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
, and it is clear that by the 1870s the term had acquired a use of its own. In 1873, for example, Willard Gibbs, in his paper “Graphical Methods in the Thermodynamics of Fluids”, states: “The quantities V, B, T, U, and S are determined when the state of the body is given, and it may be permitted to call them functions of the state of the body.”
Overview
A thermodynamic system is described by a number of thermodynamic parameters (e.g. temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, volume, pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
) which are not necessarily independent. The number of parameters needed to describe the system is the dimension of the state space
State space
In the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
of the system (
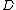). For example, a monatomic gasMonatomic gas
In physics and chemistry, monatomic is a combination of the words "mono" and "atomic," and means "single atom." It is usually applied to gases: a monatomic gas is one in which atoms are not bound to each other....
with a fixed number of particles is a simple case of a two-dimensional system (
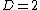). In this example, any system is uniquely specified by two parameters, such as pressure and volume, or perhaps pressure and temperature. These choices are equivalent. They are simply different coordinate systems in the two-dimensional thermodynamic state space. An analogous statement holds for higher dimensional spaces, as described by the state postulateState postulate
The state postulate is a term used in thermodynamics that defines the given number of properties to a thermodynamic system in a state of equilibrium. The state postulate allows a certain number of properties to be specified to place it in thermodynamic equilibrium...
.
When a system changes state continuously, it traces out a "path" in the state space. The path can be specified by noting the values of the state parameters as the system traces out the path, perhaps as a function of time, or some other external variable. For example, we might have the pressure
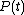and the volume 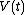as functions of time from time 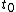to 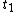. This will specify a path in our two dimensional state space example. We can now form all sorts of functions of time which we may integrate over the path. For example if we wish to calculate the work done by the system from time 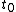to time 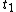we calculate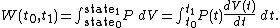It is clear that in order to calculate the work W in the above integral, we will have to know the functions
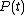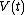and at each time , over the entire path. A state function is a function of the parameters of the system which only depends upon the parameters' values at the endpoints of the path. For example, suppose we wish to calculate the work plus the integral of 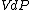over the path. We would have: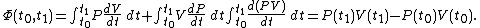It can be seen that the integrand can be expressed as the exact differential
Exact differential
A mathematical differential is said to be exact, as contrasted with an inexact differential, if it is of the form dQ, for some differentiable function Q....
of the function
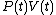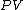and that therefore, the integral can be expressed as the difference in the value of at the end points of the integration. The product is therefore a state function of the system.By way of notation, we will specify the use of d to denote an exact differential. In other words, the integral of
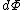will be equal to . The symbol δ will be reserved for an inexact differential, which cannot be integrated without full knowledge of the path. For example 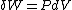will be used to denote an infinitesimal increment of work.It is best to think of state functions as quantities or properties of a thermodynamic system, while non-state functions represent a process during which the state functions change. For example, the state function
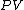is proportional to the internal energy of an ideal gas, but the work 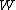is the amount of energy transferred as the system performs work. Internal energy is identifiable, it is a particular form of energy. Work is the amount of energy that has changed its form or location.List of state functions
The following are considered to be state functions in thermodynamicsThermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
:
- MassMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
(m) - EnergyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
(E)- EnthalpyEnthalpyEnthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...
(H) - Internal energyInternal energyIn thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
(U) - Gibbs free energyGibbs free energyIn thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
(G) - Helmholtz free energyHelmholtz free energyIn thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
(A) - ExergyExergyIn thermodynamics, the exergy of a system is the maximum useful work possible during a process that brings the system into equilibrium with a heat reservoir. When the surroundings are the reservoir, exergy is the potential of a system to cause a change as it achieves equilibrium with its...
- Enthalpy
- EntropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
(S)
- PressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
(p) - TemperatureThermodynamic temperatureThermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...
(T) - Volume (V)
- Chemical composition
- Specific volumeSpecific volumeIn thermodynamics, the specific volume of a substance is the ratio of the substance's volume to its mass. It is the reciprocal of density:In thermodynamics, the specific volume of a substance is the ratio of the substance's volume to its mass...
(v) or its reciprocal DensityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
(ρ) - FugacityFugacityIn chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
- AltitudeAltitudeAltitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
- Particle numberParticle numberThe particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
(ni)
See also
- Markov propertyMarkov propertyIn probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
- Conservative vector field
- Nonholonomic SystemNonholonomic systemA nonholonomic system in physics and mathematics is a system whose state depends on the path taken to achieve it. Such a system is described by a set of parameters subject to differential constraints, such that when the system evolves along a path in its parameter space but finally returns to the...
- Equation of stateEquation of stateIn physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...