
Standard normal table
Encyclopedia
A standard normal table also called the "Unit Normal Table" is a mathematical table
for the values of Φ, the cumulative distribution function
of the normal distribution.
They are used to find the probability that a statistic is observed below, above, or between values on the standard normal distribution, and by extension, any normal distribution.
Normal distributions are symmetrical, bell-shaped distributions that are useful in describing real-world data. The standard normal distribution, represented by the letter Z, is the normal distribution having a mean
of 0 and a standard deviation
of 1. Since probability tables cannot be printed for every normal distribution, (as there are infinitely many such distributions), it is common practice to convert a normal to a standard normal, and use a Z table to find probabilities.
Cumulative: This is most common, and gives Prob(Z ≤ 1.57) = 0.9418.
Complementary cumulative: The complement (1–x) of above: Prob(Z ≥ 1.57) = .0582.
Cumulative from zero: The cumulative probability, starting from 0: Prob (0 ≤ Z ≤ 1.57) = .4418
These can easily be checked by inspecting a number like 2.99:
Printed tables usually give cumulative probabilities, the chance that a statistic takes a value less than or equal to a number, from at least 0.00 to 2.99 by 1/100. To read the value 1.57 on a typical table, go to 1.5 down and 0.07 across.
The probability of Z ≤ 1.57 = 0.9418.
If your table does not have negative values, use symmetry to find the answer. Remember that 50% falls below and above 0.
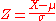
If you are using an average, divide the standard deviation by the square root of the sample size.
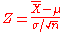
Prob(X ≤ 82) = Prob(Z ≤ (82-80)/5) = Prob(Z ≤ .40) = .6554
Prob(X ≥ 90) = Prob(Z ≥ (90-80)/5) = Prob(Z ≥ 2.00) = 1 - Prob(Z ≤ 2.00) = 1 - .9772 = .0228
Prob(X ≤ 74) = Prob(Z ≤ (74-80)/5) = Prob(Z ≤ -1.20) = .1151
If your table does not have negatives, use Prob(Z ≤ -1.20) = Prob(Z ≥ 1.20) = 1 - .8849 = .1151
Prob(78 ≤ X ≤ 88) = Prob((78-80)/5 ≤ Z ≤ (88-80)/5) = Prob(-0.40 ≤ Z ≤ 1.60) = Prob(Z ≤ 1.60) - Prob(Z ≤ -0.40) = .9452 - .3446 = .6006
Prob(X ≤ 82) = Prob(Z ≤ (82-80)/(5/√3)) = Prob(Z ≤ .69) = .7549
Mathematical table
Before calculators were cheap and plentiful, people would use mathematical tables —lists of numbers showing the results of calculation with varying arguments— to simplify and drastically speed up computation...
for the values of Φ, the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the normal distribution.
They are used to find the probability that a statistic is observed below, above, or between values on the standard normal distribution, and by extension, any normal distribution.
Normal distributions are symmetrical, bell-shaped distributions that are useful in describing real-world data. The standard normal distribution, represented by the letter Z, is the normal distribution having a mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of 0 and a standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of 1. Since probability tables cannot be printed for every normal distribution, (as there are infinitely many such distributions), it is common practice to convert a normal to a standard normal, and use a Z table to find probabilities.
Reading the table
Tables use at least 3 different conventions, depending on the interpretation of the meaning of an entry such as 1.57:Cumulative: This is most common, and gives Prob(Z ≤ 1.57) = 0.9418.
Complementary cumulative: The complement (1–x) of above: Prob(Z ≥ 1.57) = .0582.
Cumulative from zero: The cumulative probability, starting from 0: Prob (0 ≤ Z ≤ 1.57) = .4418
These can easily be checked by inspecting a number like 2.99:
- if this is approximately 1 (or rather 0.99..), then it displays cumulative probabilities;
- if this is approximately 0 (or rather 0.00..), then it displays complementary probabilities;
- if this is approximately 0.5 (or rather 0.49..), then it displays cumulative from 0 probabilities.
Printed tables usually give cumulative probabilities, the chance that a statistic takes a value less than or equal to a number, from at least 0.00 to 2.99 by 1/100. To read the value 1.57 on a typical table, go to 1.5 down and 0.07 across.
The probability of Z ≤ 1.57 = 0.9418.
If your table does not have negative values, use symmetry to find the answer. Remember that 50% falls below and above 0.
Converting from normal to standard normal
If X is a random variable from a normal distribution with mean μ and standard deviation σ, its Z-score may be calculated from X by subtracting μ and dividing by σ.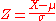
If you are using an average, divide the standard deviation by the square root of the sample size.
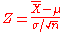
Examples
A professor's exam scores are approximately distributed normally with mean 80 and standard deviation 5.- What is the probability that a student scores an 82 or less?
Prob(X ≤ 82) = Prob(Z ≤ (82-80)/5) = Prob(Z ≤ .40) = .6554
- What is the probability that a student scores a 90 or more?
Prob(X ≥ 90) = Prob(Z ≥ (90-80)/5) = Prob(Z ≥ 2.00) = 1 - Prob(Z ≤ 2.00) = 1 - .9772 = .0228
- What is the probability that a student scores a 74 or less?
Prob(X ≤ 74) = Prob(Z ≤ (74-80)/5) = Prob(Z ≤ -1.20) = .1151
If your table does not have negatives, use Prob(Z ≤ -1.20) = Prob(Z ≥ 1.20) = 1 - .8849 = .1151
- What is the probability that a student scores between 78 and 88?
Prob(78 ≤ X ≤ 88) = Prob((78-80)/5 ≤ Z ≤ (88-80)/5) = Prob(-0.40 ≤ Z ≤ 1.60) = Prob(Z ≤ 1.60) - Prob(Z ≤ -0.40) = .9452 - .3446 = .6006
- What is the probability that an average of three scores is 82 or less?
Prob(X ≤ 82) = Prob(Z ≤ (82-80)/(5/√3)) = Prob(Z ≤ .69) = .7549
Partial Table
The below table read by using the rows to find the first digit, and the columns to find the second digit of a Z-score. To find 0.69, first look down the rows to find 0.6 and then across the columns to 0.09 and 0.7549 will be the result.| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |

