
Stable normal bundle
Encyclopedia
In surgery theory
, a branch of mathematics
, the stable normal bundle of a differentiable manifold
is an invariant which encodes the stable normal (dually, tangential) data. There are analogs for generalizations of manifold, notably PL-manifolds and topological manifold
s. There is also an analogue in homotopy theory for Poincaré space
s, the Spivak spherical fibration, named after Michael Spivak
(reference below).
(provided by the theorem of Whitney
), it has a normal bundle
. The embedding is not unique, but for high dimension of the Euclidean space it is unique up to isotopy, thus the (class of the) bundle is unique, and called the stable normal bundle.
This construction works for any Poincaré space
X: a finite CW-complex admits a stably unique (up to homotopy) embedding in Euclidean space
, via general position
, and this embedding yields a spherical fibration over X. For more restricted spaces (notably PL-manifolds and topological manifolds), one gets stronger data.
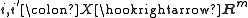 are isotopic if they are homotopic
are isotopic if they are homotopic
through embeddings. Given a manifold or other suitable space X, with two embeddings into Euclidean space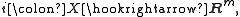
 these will not in general be isotopic, or even maps into the same space (
these will not in general be isotopic, or even maps into the same space (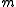 need not equal
need not equal  ). However, one can embed these into a larger space
). However, one can embed these into a larger space 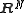 by letting the last
by letting the last 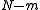 coordinates be 0:
coordinates be 0: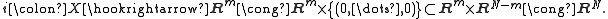
This process of adjoining trivial copies of Euclidean space is called stabilization.
One can thus arrange for any two embeddings into Euclidean space to map into the same Euclidean space (taking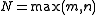 ), and, further, if
), and, further, if 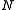 is sufficiently large, these embeddings are isotopic, which is a theorem.
is sufficiently large, these embeddings are isotopic, which is a theorem.
Thus there is a unique stable isotopy class of embedding: it is not a particular embedding (as there are many embeddings), nor an isotopy class (as the target space is not fixed: it is just "a sufficiently large Euclidean space"), but rather a stable isotopy class of maps. The normal bundle associated with this (stable class of) embeddings is then the stable normal bundle.
One can replace this stable isotopy class with an actual isotopy class by fixing the target space, either by using Hilbert space
as the target space, or (for a fixed dimension of manifold ) using a fixed
) using a fixed 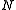 sufficiently large, as N depends only on n, not the manifold in question.
sufficiently large, as N depends only on n, not the manifold in question.
More abstractly, rather than stabilizing the embedding, one can take any embedding, and then take a vector bundle direct sum with a sufficient number of trivial line bundles; this corresponds exactly to the normal bundle of the stabilized embedding.
Construction via classifying space
An n-manifold M has a tangent bundle, which has a classifying map (up to homotopy)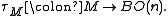
Composing with the inclusion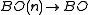 yields (the homotopy class of a classifying map of) the stable tangent bundle. The normal bundle of an embedding
yields (the homotopy class of a classifying map of) the stable tangent bundle. The normal bundle of an embedding 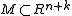 (
( large) is an inverse
large) is an inverse 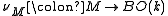 for
for 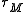 , such that the Whitney sum
, such that the Whitney sum 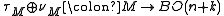 is trivial. The homotopy class of the composite
is trivial. The homotopy class of the composite
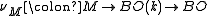 is independent of the choice of inverse,
is independent of the choice of inverse,
classifying the stable normal bundle .
.
Why stable normal, instead of stable tangent? Stable normal data is used instead of unstable tangential data because generalizations of manifolds have natural stable normal-type structures, coming from tubular neighborhood
s and generalizations, but not unstable tangential ones, as the local structure is not smooth.
Spherical fibrations over a space X are classified by the homotopy classes of maps to a
to a
classifying space
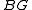 , with homotopy groups the stable homotopy groups of spheres
, with homotopy groups the stable homotopy groups of spheres

The forgetful map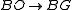 extends to a fibration
extends to a fibration
sequence
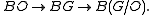
A Poincaré space
X does not have a tangent bundle, but it does have a well-defined stable spherical fibration
, which for a differentiable manifold is the spherical fibration associated to the stable normal bundle; thus a primary obstruction to X having the homotopy type of a differentiable manifold is that the spherical fibration lifts to a vector bundle, i.e. the Spivak spherical fibration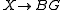 must lift to
must lift to 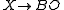 , which is equivalent to the map
, which is equivalent to the map  being null homotopic
being null homotopic
Thus the bundle obstruction to the existence of a (smooth) manifold structure is the class .
.
The secondary obstruction is the Wall surgery obstruction.
as a primary obstruction:
More generally, its generalizations serve as replacements for the (unstable) tangent bundle.
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the stable normal bundle of a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
is an invariant which encodes the stable normal (dually, tangential) data. There are analogs for generalizations of manifold, notably PL-manifolds and topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s. There is also an analogue in homotopy theory for Poincaré space
Poincaré space
In algebraic topology, a Poincaré space is an n-dimensional topological space with a distinguished element µ of its nth homology group such that taking the cap product with an element of the kth cohomology group yields an isomorphism to the th cohomology group...
s, the Spivak spherical fibration, named after Michael Spivak
Michael Spivak
Michael David Spivak is a mathematician specializing in differential geometry, an expositor of mathematics, and the founder of Publish-or-Perish Press. He is the author of the five-volume Comprehensive Introduction to Differential Geometry. He received a Ph.D...
(reference below).
Construction via embeddings
Given an embedding of a manifold in Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(provided by the theorem of Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
), it has a normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
. The embedding is not unique, but for high dimension of the Euclidean space it is unique up to isotopy, thus the (class of the) bundle is unique, and called the stable normal bundle.
This construction works for any Poincaré space
Poincaré space
In algebraic topology, a Poincaré space is an n-dimensional topological space with a distinguished element µ of its nth homology group such that taking the cap product with an element of the kth cohomology group yields an isomorphism to the th cohomology group...
X: a finite CW-complex admits a stably unique (up to homotopy) embedding in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, via general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
, and this embedding yields a spherical fibration over X. For more restricted spaces (notably PL-manifolds and topological manifolds), one gets stronger data.
Details
Two embeddings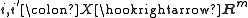 are isotopic if they are homotopic
are isotopic if they are homotopicthrough embeddings. Given a manifold or other suitable space X, with two embeddings into Euclidean space
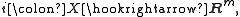
 these will not in general be isotopic, or even maps into the same space (
these will not in general be isotopic, or even maps into the same space (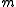 need not equal
need not equal  ). However, one can embed these into a larger space
). However, one can embed these into a larger space 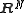 by letting the last
by letting the last 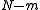 coordinates be 0:
coordinates be 0: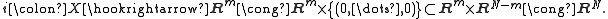
This process of adjoining trivial copies of Euclidean space is called stabilization.
One can thus arrange for any two embeddings into Euclidean space to map into the same Euclidean space (taking
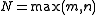 ), and, further, if
), and, further, if 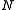 is sufficiently large, these embeddings are isotopic, which is a theorem.
is sufficiently large, these embeddings are isotopic, which is a theorem.Thus there is a unique stable isotopy class of embedding: it is not a particular embedding (as there are many embeddings), nor an isotopy class (as the target space is not fixed: it is just "a sufficiently large Euclidean space"), but rather a stable isotopy class of maps. The normal bundle associated with this (stable class of) embeddings is then the stable normal bundle.
One can replace this stable isotopy class with an actual isotopy class by fixing the target space, either by using Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
as the target space, or (for a fixed dimension of manifold
 ) using a fixed
) using a fixed 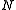 sufficiently large, as N depends only on n, not the manifold in question.
sufficiently large, as N depends only on n, not the manifold in question.More abstractly, rather than stabilizing the embedding, one can take any embedding, and then take a vector bundle direct sum with a sufficient number of trivial line bundles; this corresponds exactly to the normal bundle of the stabilized embedding.
Construction via classifying spaceClassifying spaceIn mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
s
An n-manifold M has a tangent bundle, which has a classifying map (up to homotopy)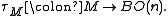
Composing with the inclusion
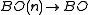 yields (the homotopy class of a classifying map of) the stable tangent bundle. The normal bundle of an embedding
yields (the homotopy class of a classifying map of) the stable tangent bundle. The normal bundle of an embedding 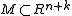 (
( large) is an inverse
large) is an inverse 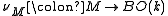 for
for 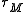 , such that the Whitney sum
, such that the Whitney sum 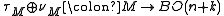 is trivial. The homotopy class of the composite
is trivial. The homotopy class of the composite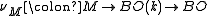 is independent of the choice of inverse,
is independent of the choice of inverse,classifying the stable normal bundle
 .
.Motivation
There is no intrinsic notion of a normal vector to a manifold, unlike tangent or cotangent vectors – for instance, the normal space depends on which dimension one is embedding into – so the stable normal bundle instead provides a notion of a stable normal space: a normal space (and normal vectors) up to trivial summands.Why stable normal, instead of stable tangent? Stable normal data is used instead of unstable tangential data because generalizations of manifolds have natural stable normal-type structures, coming from tubular neighborhood
Tubular neighborhood
In mathematics, a tubular neighborhood of a submanifold of a smooth manifold is an open set around it resembling the normal bundle.The idea behind a tubular neighborhood can be explained in a simple example. Consider a smooth curve in the plane without self-intersections. On each point on the curve...
s and generalizations, but not unstable tangential ones, as the local structure is not smooth.
Spherical fibrations over a space X are classified by the homotopy classes of maps
 to a
to aclassifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
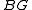 , with homotopy groups the stable homotopy groups of spheres
, with homotopy groups the stable homotopy groups of spheres
The forgetful map
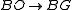 extends to a fibration
extends to a fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
sequence
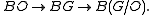
A Poincaré space
Poincaré space
In algebraic topology, a Poincaré space is an n-dimensional topological space with a distinguished element µ of its nth homology group such that taking the cap product with an element of the kth cohomology group yields an isomorphism to the th cohomology group...
X does not have a tangent bundle, but it does have a well-defined stable spherical fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
, which for a differentiable manifold is the spherical fibration associated to the stable normal bundle; thus a primary obstruction to X having the homotopy type of a differentiable manifold is that the spherical fibration lifts to a vector bundle, i.e. the Spivak spherical fibration
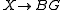 must lift to
must lift to 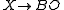 , which is equivalent to the map
, which is equivalent to the map  being null homotopic
being null homotopicThus the bundle obstruction to the existence of a (smooth) manifold structure is the class
 .
.The secondary obstruction is the Wall surgery obstruction.
Applications
The stable normal bundle is fundamental in surgery theorySurgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
as a primary obstruction:
- For a Poincaré spacePoincaré spaceIn algebraic topology, a Poincaré space is an n-dimensional topological space with a distinguished element µ of its nth homology group such that taking the cap product with an element of the kth cohomology group yields an isomorphism to the th cohomology group...
X to have the homotopy type of a smooth manifold, the map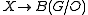 must be null homotopic
must be null homotopic - For a homotopy equivalence
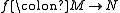 between two manifolds to be homotopic to a diffeomorphism, it must pull back the stable normal bundle on N to the stable normal bundle on M.
between two manifolds to be homotopic to a diffeomorphism, it must pull back the stable normal bundle on N to the stable normal bundle on M.
More generally, its generalizations serve as replacements for the (unstable) tangent bundle.

