
Spiral
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a spiral is a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
which emanates from a central point, getting progressively farther away as it revolves around the point.
Spiral or helix
While a "spiral" and a "helixHelix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
" are distinct as technical terms, a helix is sometimes described as a spiral in non-technical usage. The two primary definitions of a spiral are provided by the American Heritage Dictionary:
a. A curve on a plane that winds around a fixed center point at a continuously increasing or decreasing distance from the point.
b. A three-dimensional curve that turns around an axis at a varying distance while moving parallel to the axis.
The first definition is for a planar
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
curve that extends primarily in length and width, but not in height. A groove on a record
Gramophone record
A gramophone record, commonly known as a phonograph record , vinyl record , or colloquially, a record, is an analog sound storage medium consisting of a flat disc with an inscribed, modulated spiral groove...
or the arms of a spiral galaxy
Spiral galaxy
A spiral galaxy is a certain kind of galaxy originally described by Edwin Hubble in his 1936 work The Realm of the Nebulae and, as such, forms part of the Hubble sequence. Spiral galaxies consist of a flat, rotating disk containing stars, gas and dust, and a central concentration of stars known as...
(a Logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
) are examples of a spiral.
The second definition is for the 3-Dimensional variant of a spiral, for example a conical spring (device)
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
can be described as a spiral whereas a cylindrical spring or strand of a DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
are examples of a helix.
The length and width of a helix typically remain static and do not grow like on a planar spiral. If they do, then the helix becomes a conic helix. You can make a conic helix with an Archimedean or equiangular spiral by giving height to the center point, thereby creating a cone-shape from the spiral.
In the side picture, the black curve at the bottom is an Archimedean spiral
Archimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
, while the green curve is a helix. A cross between a spiral and a helix, such as the curve shown in red, is known as a conic helix. The spring used to hold and make contact with the negative terminals of AA or AAA batteries in remote controls and the vortex that is created when water is draining in a sink are examples of conic helices.
Two-dimensional spirals
A two-dimensional spiral may be described most easily using polar coordinates, where the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r is a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
monotonic function of angle θ. The circle would be regarded as a degenerate case (the function not being strictly monotonic, but rather constant).
Some of the more important sorts of two-dimensional spirals include:
- The Archimedean spiralArchimedean spiralThe Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
: (see also:InvoluteInvoluteIn the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
(see also:InvoluteInvoluteIn the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
) - The Euler spiralEuler spiralAn Euler spiral is a curve whose curvature changes linearly with its curve length . Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals....
, Cornu spiral or clothoid - Fermat's spiral:
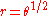
- The hyperbolic spiralHyperbolic spiralthumb|200px|right|Hyperbolic spiral for a=2A hyperbolic spiral is a transcendental plane curve also known as a reciprocal spiral. A hyperbolic spiral is the opposite of an Archimedean spiral and are a type of Cotes' spiral.It has the polar equation:...
:
- The lituusLituus (mathematics)thumb|300px|Branch for positive rIn mathematics, a lituus is a spiral in which the angle is inversely proportional to the square of the radius .r^2\theta = k \,...
: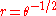
- The logarithmic spiralLogarithmic spiralA logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
: ; approximations of this are found in nature
; approximations of this are found in nature - The Fibonacci spiral and golden spiralGolden spiralIn geometry, a golden spiral is a logarithmic spiral whose growth factor is , the golden ratio. That is, a golden spiral gets wider by a factor of for every quarter turn it makes.-Formula:...
: special cases of the logarithmic spiral - The Spiral of TheodorusSpiral of TheodorusIn geometry, the spiral of Theodorus is a spiral composed of contiguous right triangles. It was first constructed by Theodorus of Cyrene.-Construction:...
: an approximation of the Archimedean spiral composed of contiguous right triangles
Three-dimensional spirals
For simple 3-d spirals, a third variable, h (height), is also a continuous, monotonic functionMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
of θ. For example, a conic helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
may be defitned as a spiral on a conic surface, with the distance to the apex an exponential function of θ.
The helix and vortex
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
can be viewed as a kind of three-dimensional
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
spiral.
For a helix with thickness, see spring (math).
Another kind of spiral is a conic spiral along a circle. This spiral is formed along the surface of a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
whose axis is bent and restricted to a circle:
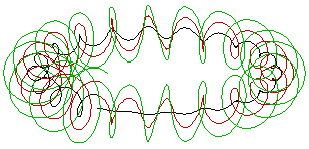
This image is reminiscent of a Ouroboros
Ouroboros
The Ouroboros is an ancient symbol depicting a serpent or dragon eating its own tail. The name originates from within Greek language; οὐρά meaning "tail" and βόρος meaning "eating", thus "he who eats the tail"....
symbol and could be mistaken for a torus with a continuously-increasing diameter:

Spherical spiral
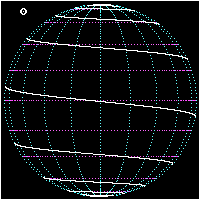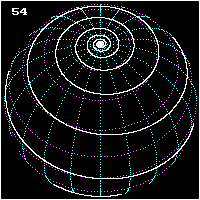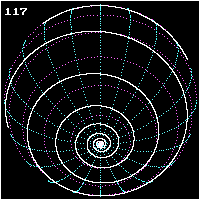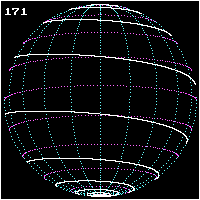
Rhumb line
In navigation, a rhumb line is a line crossing all meridians of longitude at the same angle, i.e. a path derived from a defined initial bearing...
or loxodrome, left picture) is the curve on a sphere traced by a ship traveling from one pole to the other while keeping a fixed angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
(unequal to 0° and to 90°) with respect to the meridians of longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
, i.e. keeping the same bearing
Bearing (navigation)
In marine navigation, a bearing is the direction one object is from another object, usually, the direction of an object from one's own vessel. In aircraft navigation, a bearing is the actual compass direction of the forward course of the aircraft...
. The curve has an infinite number of revolutions, with the distance between them decreasing as the curve approaches either of the poles.
The gap between the curves of an Archimedean spiral
Archimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
(right picture) remains constant as the radius changes and hence is not a rhumb line.
As a symbol

Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
ism, and appears in megalithic art, notably in the Newgrange
Newgrange
Newgrange is a prehistoric monument located in County Meath, on the eastern side of Ireland, about one kilometre north of the River Boyne. It was built around 3200 BC , during the Neolithic period...
tomb or in many Galician petroglyphs such as the one in Mogor. See, for example, the triple spiral
Triple spiral
The triple spiral or triskele is a Celtic and pre-Celtic symbol found on a number of Irish Megalithic and Neolithic sites, most notably inside the Newgrange passage tomb, on the entrance stone, and on some of the curbstones surrounding the mound....
.
While scholars are still debating the subject, there is a growing acceptance that the simple spiral, when found in Chinese art, is an early symbol for the sun. Roof tiles dating back to the Tang Dynasty
Tang Dynasty
The Tang Dynasty was an imperial dynasty of China preceded by the Sui Dynasty and followed by the Five Dynasties and Ten Kingdoms Period. It was founded by the Li family, who seized power during the decline and collapse of the Sui Empire...
with this symbol have been found west of the ancient city of Chang'an
Chang'an
Chang'an is an ancient capital of more than ten dynasties in Chinese history, today known as Xi'an. Chang'an literally means "Perpetual Peace" in Classical Chinese. During the short-lived Xin Dynasty, the city was renamed "Constant Peace" ; yet after its fall in AD 23, the old name was restored...
(modern-day Xian).
Spirals are also a symbol of hypnosis
Hypnosis
Hypnosis is "a trance state characterized by extreme suggestibility, relaxation and heightened imagination."It is a mental state or imaginative role-enactment . It is usually induced by a procedure known as a hypnotic induction, which is commonly composed of a long series of preliminary...
, stemming from the cliché
Cliché
A cliché or cliche is an expression, idea, or element of an artistic work which has been overused to the point of losing its original meaning or effect, especially when at some earlier time it was considered meaningful or novel. In phraseology, the term has taken on a more technical meaning,...
of people and cartoon characters being hypnotized by staring into a spinning spiral (One example being Kaa
Kaa
Kaa is a fictional and exceptionally long Python molurus from the Mowgli stories written by Rudyard Kipling. Kaa is one of Mowgli's mentors and friends. He, Baloo and Bagheera sing for Mowgli "The Outsong" of the jungle. First introduced in the story "Kaa's Hunting" in The Jungle Book, Kaa is a...
in Disney's The Jungle Book
The Jungle Book (1967 film)
The Jungle Book is a 1967 American animated film produced by Walt Disney Animation Studios. Released on October 18, 1967, it is the 19th animated feature in the Walt Disney Animated Classics series. It was inspired by the stories about the feral child Mowgli from the book of the same name by...
). They are also used as a symbol of dizziness
Dizziness
Dizziness refers to an impairment in spatial perception and stability. The term is somewhat imprecise. It can be used to mean vertigo, presyncope, disequilibrium, or a non-specific feeling such as giddiness or foolishness....
, where the eyes of a cartoon character, especially in anime
Anime
is the Japanese abbreviated pronunciation of "animation". The definition sometimes changes depending on the context. In English-speaking countries, the term most commonly refers to Japanese animated cartoons....
and manga
Manga
Manga is the Japanese word for "comics" and consists of comics and print cartoons . In the West, the term "manga" has been appropriated to refer specifically to comics created in Japan, or by Japanese authors, in the Japanese language and conforming to the style developed in Japan in the late 19th...
, will turn into spirals to show they are dizzy or dazed. The spiral is also found in structures as small as the double helix structure of DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
and as large as the spiral structure of a galaxy
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
.
The spiral is also a symbol of the process of dialectic
Dialectic
Dialectic is a method of argument for resolving disagreement that has been central to Indic and European philosophy since antiquity. The word dialectic originated in Ancient Greece, and was made popular by Plato in the Socratic dialogues...
.
In nature

Nature
Nature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
have a long history, Christopher Wren
Christopher Wren
Sir Christopher Wren FRS is one of the most highly acclaimed English architects in history.He used to be accorded responsibility for rebuilding 51 churches in the City of London after the Great Fire in 1666, including his masterpiece, St. Paul's Cathedral, on Ludgate Hill, completed in 1710...
observed that many shells form a logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
. Jan Swammerdam
Jan Swammerdam
Jan Swammerdam was a Dutch biologist and microscopist. His work on insects demonstrated that the various phases during the life of an insect—egg, larva, pupa, and adult—are different forms of the same animal. As part of his anatomical research, he carried out experiments on muscle contraction...
observed the common mathematical characteristics of a wide range of shells from Helix
Helix (genus)
Helix is a genus of large air-breathing land snails, terrestrial pulmonate gastropod molluscs. This genus is native to Europe and the regions around the Mediterranean Sea. Helix is the type genus of the family Helicidae....
to Spirula and Henry Nottidge Moseley
Henry Nottidge Moseley
Henry Nottidge Moseley, FRS was a British naturalist who sailed on the global scientific expedition of the HMS Challenger in 1872 through 1876....
described the mathematics of univalve shells. D’Arcy Wentworth Thompson
D'Arcy Wentworth Thompson
Sir D'Arcy Wentworth Thompson CB FRS FRSE was a Scottish biologist, mathematician, and classics scholar. A pioneering mathematical biologist, he is mainly remembered as the author of the 1917 book On Growth and Form, written largely in Dundee in 1915...
's On Growth and Form gives extensive treatment to these spirals. He describes how shells are formed by rotating a closed curve around a fixed axis, the shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
of the curve remains fixed but its size grows in a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
. In some shell such as Nautilus
Nautilus
Nautilus is the common name of marine creatures of cephalopod family Nautilidae, the sole extant family of the superfamily Nautilaceae and of its smaller but near equal suborder, Nautilina. It comprises six living species in two genera, the type of which is the genus Nautilus...
and ammonite
Ammonite
Ammonite, as a zoological or paleontological term, refers to any member of the Ammonoidea an extinct subclass within the Molluscan class Cephalopoda which are more closely related to living coleoids Ammonite, as a zoological or paleontological term, refers to any member of the Ammonoidea an extinct...
s the generating curve revolves in a plane perpendicular to the axis and the shell will form a planar discoid shape. In others it follows a skew path forming a helico
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
-spiral pattern.
Thompson also studied spirals occurring in horn
Horn (anatomy)
A horn is a pointed projection of the skin on the head of various animals, consisting of a covering of horn surrounding a core of living bone. True horns are found mainly among the ruminant artiodactyls, in the families Antilocapridae and Bovidae...
s, teeth, claw
Claw
A claw is a curved, pointed appendage, found at the end of a toe or finger in most mammals, birds, and some reptiles. However, the word "claw" is also often used in reference to an invertebrate. Somewhat similar fine hooked structures are found in arthropods such as beetles and spiders, at the end...
s and plant
Plant
Plants are living organisms belonging to the kingdom Plantae. Precise definitions of the kingdom vary, but as the term is used here, plants include familiar organisms such as trees, flowers, herbs, bushes, grasses, vines, ferns, mosses, and green algae. The group is also called green plants or...
s.
Spirals in plants and animals are frequently described as whorls
Whorl (botany)
In botany, a whorl is an arrangement of sepals, petals, leaves, or branches in which all the parts are attached at the same point and surround or wrap around the stem.There are four whorls in a general flower...
. This is also the name given to spiral shaped fingerprints.
A model for the pattern of florets in the head of a sunflower
Sunflower
Sunflower is an annual plant native to the Americas. It possesses a large inflorescence . The sunflower got its name from its huge, fiery blooms, whose shape and image is often used to depict the sun. The sunflower has a rough, hairy stem, broad, coarsely toothed, rough leaves and circular heads...
was proposed by H Vogel. This has the form
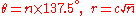
where n is the index number of the floret and c is a constant scaling factor, and is a form of Fermat's spiral. The angle 137.5° is related to the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and gives a close packing of florets.
In art
The spiral has inspired artists throughout the ages. Among the most famous of spiral-inspired art is Robert SmithsonRobert Smithson
Robert Smithson was an American artist famous for his land art.-Background and education:Smithson was born in Passaic, New Jersey and studied painting and drawing in New York City at the Art Students League of New York....
's earthwork, "Spiral Jetty
Spiral Jetty
The Spiral Jetty, considered to be the central work of American sculptor Robert Smithson, is an earthwork sculpture constructed in 1970.Built entirely of mud, salt crystals, basalt rocks, earth, and water on the northeastern shore of the Great Salt Lake near Rozel Point in Utah, it forms a , ...
", at the Great Salt Lake
Great Salt Lake
The Great Salt Lake, located in the northern part of the U.S. state of Utah, is the largest salt water lake in the western hemisphere, the fourth-largest terminal lake in the world. In an average year the lake covers an area of around , but the lake's size fluctuates substantially due to its...
in Utah. The spiral theme is also present in David Wood's Spiral Resonance Field at the Balloon Museum
Anderson-Abruzzo Albuquerque International Balloon Museum
The Anderson-Abruzzo Albuquerque International Balloon Museum is a museum dedicated to the worldwide history, science, and art of all types of ballooning and lighter-than-air flight...
in Albuquerque, as well as in the critically acclaimed Nine Inch Nails
Nine Inch Nails
Nine Inch Nails is an American industrial rock project, founded in 1988 by Trent Reznor in Cleveland, Ohio. As its main producer, singer, songwriter, and instrumentalist, Reznor is the only official member of Nine Inch Nails and remains solely responsible for its direction...
1994 concept album The Downward Spiral
The Downward Spiral
The Downward Spiral is the second studio album by American industrial rock act Nine Inch Nails, released March 8, 1994, on Interscope Records. It is a concept album detailing the destruction of a man, from the beginning of his "downward spiral" to his climactic attempt at suicide...
.
External links
- SpiralZoom.com, an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.

