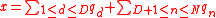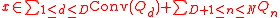Shapley–Folkman lemma
Encyclopedia
In geometry
and economics
, the Shapley–Folkman lemma
describes the Minkowski addition of sets in a vector space
. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integer
s zero and one to itself yields the set consisting of zero, one, and two:
The Shapley–Folkman lemma and related results provide an affirmative answer to the question, "Is the sum of many sets close to being convex
?" A set is defined to be convex if every line segment
joining two of its points is a subset
in the set: For example, the solid disk is a convex set but the circle
is a convex set but the circle
 is not, because the line segment joining two distinct points
is not, because the line segment joining two distinct points  is not a subset of the circle. The Shapley–Folkman lemma suggests that if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.
is not a subset of the circle. The Shapley–Folkman lemma suggests that if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.
The Shapley–Folkman lemma was introduced as a step in the proof
of the Shapley–Folkman theorem
, which states an upper bound
on the distance
between the Minkowski sum and its convex hull
. The convex hull of a set Q is the smallest convex set that contains Q. This distance is zero if and only if
the sum is convex.
The theorem's bound on the distance depends on the dimension D and on the shapes of the summand-sets, but not on the number of summand-sets N,
The shapes of a subcollection of only D summand-sets determine the bound on the distance between the Minkowski average
of N sets
and its convex hull. As N increases to infinity
, the bound decreases to zero
(for summand-sets of uniformly bounded size). The Shapley–Folkman theorem's upper bound was decreased by Starr's corollary
(alternatively, the Shapley–Folkman–Starr theorem).
The lemma of Lloyd Shapley
and Jon Folkman
was first published by the economist Ross M. Starr
, who was investigating the existence of economic equilibria while studying with Kenneth Arrow
. In his paper, Starr studied a convexified economy, in which non-convex sets were replaced by their convex hulls; Starr proved that the convexified economy has equilibria that are closely approximated by "quasi-equilibria" of the original economy; moreover, he proved that every quasi-equilbrium has many of the optimal properties of true equilibria, which are proved to exist for convex economies. Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used to show that central results of (convex) economic theory are good approximations to large economies with non-convexities; for example, quasi-equilibria closely approximate equilibria of a convexified economy. "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Roger Guesnerie. The topic of non-convex sets in economics
has been studied by many Nobel laureates: Arrow (1972), Robert Aumann
(2005), Gérard Debreu
(1983), Tjalling Koopmans
(1975), Paul Krugman
(2008), and Paul Samuelson
(1970); the complementary topic of convex sets in economics
has been emphasized by these laureates, along with Leonid Hurwicz
, Leonid Kantorovich
(1975), and Robert Solow
(1987).
The Shapley–Folkman lemma has applications also in optimization and probability theory
. In optimization theory, the Shapley–Folkman lemma has been used to explain the successful solution of minimization problems that are sums of many function
s. The Shapley–Folkman lemma has also been used in proofs
of the "law of averages"
for random sets
, a theorem that had been proved for only convex sets.
of real number
s [0, 2], which is convex. The Shapley–Folkman lemma implies that every point in [0, 2] is the sum of an integer from {0, 1} and a real number from [0, 1].
The distance between the convex interval [0, 2] and the non-convex set {0, 1, 2} equals one-half
However, the distance between the average
Minkowski sum
and its convex hull [0, 1] is only 1/4, which is half the distance (1/2) between its summand {0, 1} and [0, 1]. As more sets are added together, the average of their sum "fills out" its convex hull: The maximum distance between the average and its convex hull approaches zero as the average includes more summands.
.
vector space
of two dimension
s can be given a Cartesian coordinate system
in which every point is identified by an ordered pair
of real numbers, called "coordinates", which are conventionally denoted by x and y. Two points in the Cartesian plane can be added coordinate-wise
further, a point can be multiplied
by each real number λ coordinate-wise
More generally, any real vector space of (finite) dimension D can be viewed as the set of all D-tuple
s of D real numbers } on which two operation
s are defined: vector addition and multiplication by a real number
. For finite-dimensional vector spaces, the operations of vector addition and real-number multiplication can each be defined coordinate-wise, following the example of the Cartesian plane.
set Q is defined to be convex
if, for each pair of its points, every point on the line segment
that joins them is a subset
of Q. For example, a solid disk is convex but a circle
is convex but a circle
 is not, because it does not contain a line segment joining its points
is not, because it does not contain a line segment joining its points  ; the non-convex set of three integers {0, 1, 2} is contained in the interval [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
; the non-convex set of three integers {0, 1, 2} is contained in the interval [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
shape, is non-convex. The empty set is convex, either by definition or vacuously
, depending on the author.
More formally, a set Q is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval
[0,1], the point
is a member of Q.
By mathematical induction
, a set Q is convex if and only if every convex combination
of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, . . . , vD} of a vector space is any weighted average for some indexed set of non-negative real numbers {λd} satisfying the equation = 1.
The definition of a convex set implies that the intersection
of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.
 For every subset Q of a real vector space, its is the minimal convex set that contains Q. Thus Conv(Q) is the intersection of all the convex sets that cover Q. The convex hull of a set can be equivalently defined to be the set of all convex combinations of points in Q. For example, the convex hull of the set of integer
For every subset Q of a real vector space, its is the minimal convex set that contains Q. Thus Conv(Q) is the intersection of all the convex sets that cover Q. The convex hull of a set can be equivalently defined to be the set of all convex combinations of points in Q. For example, the convex hull of the set of integer
s {0,1} is the closed interval
of real number
s [0,1], which contains the integer end-points. The convex hull of the unit circle
is the closed unit disk, which contains the unit circle.
of two (non-empty) sets Q1 and Q2 is defined to be the set
Q1 + Q2 formed by the addition of vectors element-wise from the summand sets
For example
By the principle of mathematical induction, the Minkowski sum of a finite family of (non-empty) sets
is the
set
formed by element-wise addition of vectors
of their Minkowski sum is the Minkowski sum of their convex hulls. That is,
This result holds more generally, as a consequence of the principle of mathematical induction. For each finite collection of sets,
Conv( ∑ Qn ) = ∑ Conv( Qn )
implies that
if a point x lies in the convex hull of the Minkowski sum of N sets
then x lies in the sum of the convex hulls of the summand-sets
By the definition of Minkowski addition, this last expression means that x = ∑ qn for some selection of points qn in the convex hulls of the summand-sets, that is, where each qn ∈ Conv(Qn). In this representation, the selection of the summand-points qn depends on the chosen sum-point x.
.jpg) For this representation of the point x, the Shapley–Folkman lemma states that if the dimension D is less than the number of summands
For this representation of the point x, the Shapley–Folkman lemma states that if the dimension D is less than the number of summands
then convexification is needed for only D summand-sets, whose choice depends on x: The point has a representation
where qd belongs to the convex hull of Qd for D (or fewer) summand-sets and qn belongs to Qn itself for the remaining sets. That is,
for some re-indexing of the summand sets; this re-indexing depends on the particular point x being represented.
The Shapley–Folkman lemma implies, for example, that every point in [0, 2] is the sum of an integer
from {0, 1} and a real number
from [0, 1].
of finite-dimensional, real vector spaces. That is, if a vector space obeys the Shapley–Folkman lemma for a natural number
D, and for no number less than D, then its dimension is exactly D; the Shapley–Folkman lemma holds for only finite-dimensional vector spaces.
The Shapley–Folkman theorem states a bound on the distance between the Minkowski sum and its convex hull; this distance is zero if and only if
the sum is convex. Their bound on the distance depends on the dimension D and on the shapes of the summand-sets, but not on the number of summand-sets N,
The circumradius often exceeds (and cannot be less than) the inner radius:
Starr used the inner radius to reduce the upper bound stated in the Shapley–Folkman theorem:
Starr's corollary states an upper bound on the Euclidean distance between the Minkowski sum of N sets and the convex hull of the Minkowski sum; this distance between the sum and its convex hull is a measurement of the non-convexity of the set. For simplicity
, this distance is called the "non-convexity" of the set (with respect to Starr's measurement). Thus, Starr's bound on the non-convexity of the sum depends on only the D largest inner radii of the summand-sets; however, Starr's bound does not depend on the number of summand-sets N, when .
For example, the distance between the convex interval [0, 2] and the non-convex set {0, 1, 2} equals one-half
Thus, Starr's bound on the non-convexity of the average
decreases as the number of summands N increases.
For example, the distance between the averaged set
and its convex hull [0, 1] is only 1/4, which is half the distance (1/2) between its summand {0, 1} and [0, 1].
The shapes of a subcollection of only D summand-sets determine the bound on the distance between the average set and its convex hull; thus, as the number of summands increases to infinity
, the bound decreases to zero
(for summand-sets of uniformly bounded size). In fact, Starr's bound on the non-convexity of this average set decreases to zero
as the number of summands N increases to infinity
(when the inner radii of all the summands are bounded by the same number).
of the representation, but did not provide an algorithm
for computing the representation: Similar proofs have been given by Arrow
and Hahn
, Cassels
, and Schneider, among others. An abstract and elegant proof by Ekeland
has been extended by Artstein. Different proofs have appeared in unpublished papers, also. In 1981, Starr published an iterative method
for computing a representation of a given sum-point; however, his computational proof provides a weaker bound than does the original result.
, in mathematical optimization, and in probability theory
; in each of these three mathematical sciences, non-convexity is an important feature of applications.
, a consumer's preferences
are defined over all "baskets" of goods. Each basket is represented as a non-negative vector, whose coordinates represent the quantities of the goods. On this set of baskets, an indifference curve
is defined for each consumer; a consumer's indifference curve contains all the baskets of commodities that the consumer regards as equivalent: That is, for every pair of baskets on the same indifference curve, the consumer does not prefer one basket over another. Through each basket of commodities passes one indifference curve. A consumer's preference set (relative to an indifference curve) is the union
of the indifference curve and all the commodity baskets that the consumer prefers over the indifference curve. A consumer's preferences are convex if all such preference sets are convex.
An optimal basket of goods occurs where the budget-line supports
a consumer's preference set, as shown in the diagram. This means that an optimal basket is on the highest possible indifference curve given the budget-line, which is defined in terms of a price vector and the consumer's income (endowment vector). Thus, the set of optimal baskets is a function
of the prices, and this function is called the consumer's demand
. If the preference set is convex, then at every price the consumer's demand is a convex set, for example, a unique optimal basket or a line-segment of baskets.
)! Thus, the zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.
When the consumer's preference set is non-convex, then (for some prices) the consumer's demand is not connected
; a disconnected demand implies some discontinuous behavior by the consumer, as discussed by Harold Hotelling
:
The difficulties of studying non-convex preferences were emphasized by Herman Wold
and again by Paul Samuelson
, who wrote that non-convexities are "shrouded in eternal according to Diewert.
Nonetheless, non-convex preferences were illuminated from 1959 to 1961 by a sequence of papers in The Journal of Political Economy (JPE). The main contributors were Farrell, Bator, Koopmans
, and Rothenberg. In particular, Rothenberg's paper discussed the approximate convexity of sums of non-convex sets. These JPE-papers stimulated a paper by Lloyd Shapley
and Martin Shubik
, which considered convexified consumer-preferences and introduced the concept of an "approximate equilibrium". The JPE-papers and the Shapley–Shubik paper influenced another notion of "quasi-equilibria", due to Robert Aumann
.
 Previous publications on non-convexity and economics
Previous publications on non-convexity and economics
were collected in an annotated bibliography by Kenneth Arrow
. He gave the bibliography to Starr
, who was then an undergraduate enrolled in Arrow's (graduate) advanced mathematical-economics course. In his term-paper, Starr studied the general equilibria of an artificial economy in which non-convex preferences were replaced by their convex hulls. In the convexified economy, at each price, the aggregate demand
was the sum of convex hulls of the consumers' demands. Starr's ideas interested the mathematicians Lloyd Shapley
and Jon Folkman
, who proved their eponym
ous lemma and theorem in "private correspondence", which was reported by Starr's published paper of 1969.
In his 1969 publication, Starr applied the Shapley–Folkman–Starr theorem. Starr proved that the "convexified" economy has general equilibria that can be closely approximated by "quasi-equilbria" of the original economy, when the number of agents exceeds the dimension of the goods: Concretely, Starr proved that there exists at least one quasi-equilibrium of prices popt with the following properties:
Starr established that
Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used in economic theory. Roger Guesnerie
summarized their economic implications: "Some key results obtained under the convexity assumption remain (approximately) relevant in circumstances where convexity fails. For example, in economies with a large consumption side, preference nonconvexities do not destroy the standard results". "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Guesnerie. The topic of non-convex sets in economics
has been studied by many Nobel laureates: Arrow (1972), Robert Aumann
(2005), Gérard Debreu
(1983), Tjalling Koopmans
(1975), Paul Krugman
(2008), and Paul Samuelson
(1970); the complementary topic of convex sets in economics
has been emphasized by these laureates, along with Leonid Hurwicz
, Leonid Kantorovich
(1975), and Robert Solow
(1987). The Shapley–Folkman–Starr results have been featured in the economics literature: in microeconomics
, in general-equilibrium theory, in public economics (including market failure
s), as well as in game theory
, in mathematical economics
, and in applied mathematics (for economists). The Shapley–Folkman–Starr results have also influenced economics research using measure
and integration theory
.
problems with non-convexities
can be nearly solved (with iterative methods whose convergence proofs are stated for only convex problems).
relies on the following definitions for function
s:
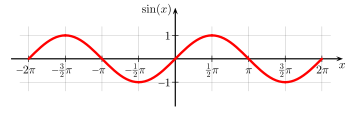
For example, the quadratic function f(x) = x2 is convex, as is the absolute value function g(x) = |x|. However, the sine function
(pictured) is non-convex on the interval (0, π).
For example, problems of linear optimization
are separable. Given a separable problem with an optimal solution, we fix an optimal solution
with the minimum value For this separable problem, we also consider an optimal solution (xmin, f(xmin) )
to the "convexified problem", where convex hulls are taken of the graphs of the summand functions. Such an optimal solution is the limit of a sequence
of points in the convexified problem
Of course, the given optimal-point is a sum of points in the graphs of the original summands and of a small number of convexified summands, by the Shapley–Folkman lemma.
This analysis was published by Ivar Ekeland
in 1974 to explain the apparent convexity of separable problems with many summands, despite the non-convexity of the summand problems. In 1973, the young mathematician Claude Lemaréchal
was surprised by his success with convex minimization method
s on problems that were known to be non-convex; for minimizing nonlinear
problems, a solution of the dual problem
problem need not provide useful information for solving the primal problem, unless the primal problem be convex and satisfy a constraint qualification. Lemaréchal's problem was additively separable, and each summand function was non-convex; nonetheless, a solution to the dual problem provided a close approximation to the primal problem's optimal value. Ekeland's analysis explained the success of methods of convex minimization on large and separable problems, despite the non-convexities of the summand functions. Ekeland and later authors argued that additive separability produced an approximately convex aggregate problem, even though the summand functions were non-convex. The crucial step in these publications is the use of the Shapley–Folkman lemma.
The Shapley–Folkman lemma has encouraged the use of methods of convex minimization on other applications with sums of many functions.
. Each point in the convex hull of a (non-empty
) subset Q of a finite-dimensional space is the expected value
of a simple
random vector
that takes its values in Q, as a consequence of Carathéodory's lemma
. Thus, for a non-empty set Q, the collection of the expected values of the simple, Q-valued random vectors equals Q convex hull; this equality implies that the Shapley–Folkman–Starr results are useful in probability theory. In the other direction, probability theory provides tools to examine convex sets generally and the Shapley–Folkman–Starr results specifically. The Shapley–Folkman–Starr results have been widely used in the probabilistic theory of random sets
, for example, to prove a law of large numbers
, a central limit theorem
, and a large-deviations
principle
. These proofs of probabilistic limit theorems
used the Shapley–Folkman–Starr results to avoid the assumption that all the random sets be convex.
A probability measure
is a finite measure
, and the Shapley–Folkman lemma has applications in non-probabilistic measure theory, such as the theories of volume
and of vector measure
s. The Shapley–Folkman lemma enables a refinement of the Brunn–Minkowski inequality, which bounds the volume of sums in terms of the volumes of their summand-sets. The volume of a set is defined in terms of the Lebesgue measure, which is defined on subsets of Euclidean space
. In advanced measure-theory, the Shapley–Folkman lemma has been used to prove Lyapunov's theorem, which states that the range
of a vector measure is convex. Here, the traditional term "range" (alternatively, "image") is the set of values produced by the function. A vector measure is a vector-valued generalization of a measure; for example, if p1 and p2 are probability measure
s defined on the same measurable space, then the product function is a vector measure,
where
is defined for every event
ω
by
Lyapunov's theorem has been used in economics
, in ("bang-bang") control theory
, and in statistical theory
. Lyapunov's theorem has been called a continuous
counterpart of the Shapley–Folkman lemma, which has itself been called a discrete analogue of Lyapunov's theorem.
Convex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
and economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
, the Shapley–Folkman lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
describes the Minkowski addition of sets in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s zero and one to itself yields the set consisting of zero, one, and two:
- {0, 1} + {0, 1} = {0 + 0, 0 + 1, 1 + 0, 1 + 1} = {0, 1, 2}.
The Shapley–Folkman lemma and related results provide an affirmative answer to the question, "Is the sum of many sets close to being convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
?" A set is defined to be convex if every line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
joining two of its points is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
in the set: For example, the solid disk
 is a convex set but the circle
is a convex set but the circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
 is not, because the line segment joining two distinct points
is not, because the line segment joining two distinct points  is not a subset of the circle. The Shapley–Folkman lemma suggests that if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.
is not a subset of the circle. The Shapley–Folkman lemma suggests that if the number of summed sets exceeds the dimension of the vector space, then their Minkowski sum is approximately convex.The Shapley–Folkman lemma was introduced as a step in the proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of the Shapley–Folkman theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
, which states an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between the Minkowski sum and its convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
. The convex hull of a set Q is the smallest convex set that contains Q. This distance is zero if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the sum is convex.
The theorem's bound on the distance depends on the dimension D and on the shapes of the summand-sets, but not on the number of summand-sets N,
The shapes of a subcollection of only D summand-sets determine the bound on the distance between the Minkowski average
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of N sets
- (Q1 + Q2 + ... + QN)
and its convex hull. As N increases to infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, the bound decreases to zero
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
(for summand-sets of uniformly bounded size). The Shapley–Folkman theorem's upper bound was decreased by Starr's corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
(alternatively, the Shapley–Folkman–Starr theorem).
The lemma of Lloyd Shapley
Lloyd Shapley
Lloyd Stowell Shapley is a distinguished American mathematician and economist. He is a Professor Emeritus at University of California, Los Angeles, affiliated with departments of Mathematics and Economics...
and Jon Folkman
Jon Folkman
Jon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.-Schooling:Folkman was a Putnam Fellow in 1960. He received his Ph.D...
was first published by the economist Ross M. Starr
Ross Starr
Ross Starr is an American economist who specializes in microeconomic theory, monetary economics and mathematical economics. He is a Professor at the University of California, San Diego....
, who was investigating the existence of economic equilibria while studying with Kenneth Arrow
Kenneth Arrow
Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....
. In his paper, Starr studied a convexified economy, in which non-convex sets were replaced by their convex hulls; Starr proved that the convexified economy has equilibria that are closely approximated by "quasi-equilibria" of the original economy; moreover, he proved that every quasi-equilbrium has many of the optimal properties of true equilibria, which are proved to exist for convex economies. Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used to show that central results of (convex) economic theory are good approximations to large economies with non-convexities; for example, quasi-equilibria closely approximate equilibria of a convexified economy. "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Roger Guesnerie. The topic of non-convex sets in economics
Non-convexity (economics)
In economics, non-convexity refers to violations of the convexity assumptions of elementary economics. Basic economics textbooks concentrate on consumers with convex preferences and convex budget sets and on producers with convex production sets; for convex models, the predicted economic behavior...
has been studied by many Nobel laureates: Arrow (1972), Robert Aumann
Robert Aumann
Robert John Aumann is an Israeli-American mathematician and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel...
(2005), Gérard Debreu
Gerard Debreu
Gérard Debreu was a French economist and mathematician, who also came to have United States citizenship. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 1983 Nobel Memorial Prize in Economics.-Biography:His father was the...
(1983), Tjalling Koopmans
Tjalling Koopmans
Tjalling Charles Koopmans was the joint winner, with Leonid Kantorovich, of the 1975 Nobel Memorial Prize in Economic Sciences....
(1975), Paul Krugman
Paul Krugman
Paul Robin Krugman is an American economist, professor of Economics and International Affairs at the Woodrow Wilson School of Public and International Affairs at Princeton University, Centenary Professor at the London School of Economics, and an op-ed columnist for The New York Times...
(2008), and Paul Samuelson
Paul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
(1970); the complementary topic of convex sets in economics
Convexity in economics
Convexity is an important topic in economics. In the Arrow-Debreu model of general economic equilibrium, agents have convex budget sets and convex preferences: At equilibrium prices, the budget hyperplane supports the best attainable indifference curve. The profit function is the convex conjugate...
has been emphasized by these laureates, along with Leonid Hurwicz
Leonid Hurwicz
Leonid "Leo" Hurwicz was a Russian-born American economist and mathematician. His nationality of origin was Polish. He was Jewish. He originated incentive compatibility and mechanism design, which show how desired outcomes are achieved in economics, social science and political science...
, Leonid Kantorovich
Leonid Kantorovich
Leonid Vitaliyevich Kantorovich was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources...
(1975), and Robert Solow
Robert Solow
Robert Merton Solow is an American economist particularly known for his work on the theory of economic growth that culminated in the exogenous growth model named after him...
(1987).
The Shapley–Folkman lemma has applications also in optimization and probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. In optimization theory, the Shapley–Folkman lemma has been used to explain the successful solution of minimization problems that are sums of many function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s. The Shapley–Folkman lemma has also been used in proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of the "law of averages"
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
for random sets
Stochastic geometry
In mathematics, stochastic geometry is the study of random spatial patterns. At the heart of the subject lies the study of random point patterns...
, a theorem that had been proved for only convex sets.
Introductory example
For example, the subset of the integers {0, 1, 2} is contained in the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s [0, 2], which is convex. The Shapley–Folkman lemma implies that every point in [0, 2] is the sum of an integer from {0, 1} and a real number from [0, 1].
The distance between the convex interval [0, 2] and the non-convex set {0, 1, 2} equals one-half
- 1/2 = |1-1/2| = |0-1/2| = |2-3/2| = |1-3/2|.
However, the distance between the average
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
Minkowski sum
- 1/2 ( {0, 1} + {0, 1} ) = {0, 1/2, 1}
and its convex hull [0, 1] is only 1/4, which is half the distance (1/2) between its summand {0, 1} and [0, 1]. As more sets are added together, the average of their sum "fills out" its convex hull: The maximum distance between the average and its convex hull approaches zero as the average includes more summands.
Preliminaries
The Shapley–Folkman lemma depends upon the following definitions and results from convex geometryConvex geometry
Convex geometry is the branch of geometry studying convex sets, mainly in Euclidean space.Convex sets occur naturally in many areas of mathematics: computational geometry, convex analysis, discrete geometry, functional analysis, geometry of numbers, integral geometry, linear programming,...
.
Real vector spaces
A realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of two dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
s can be given a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
in which every point is identified by an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of real numbers, called "coordinates", which are conventionally denoted by x and y. Two points in the Cartesian plane can be added coordinate-wise
- (x1, y1) + (x2, y2) = (x1+x2, y1+y2);
further, a point can be multiplied
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by each real number λ coordinate-wise
- λ (x, y) = (λx, λy).
More generally, any real vector space of (finite) dimension D can be viewed as the set of all D-tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of D real numbers } on which two operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s are defined: vector addition and multiplication by a real number
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
. For finite-dimensional vector spaces, the operations of vector addition and real-number multiplication can each be defined coordinate-wise, following the example of the Cartesian plane.
Convex sets
In a real vector space, a non-emptyEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
set Q is defined to be convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
if, for each pair of its points, every point on the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
that joins them is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Q. For example, a solid disk
 is convex but a circle
is convex but a circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
 is not, because it does not contain a line segment joining its points
is not, because it does not contain a line segment joining its points  ; the non-convex set of three integers {0, 1, 2} is contained in the interval [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
; the non-convex set of three integers {0, 1, 2} is contained in the interval [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescentCrescent
In art and symbolism, a crescent is generally the shape produced when a circular disk has a segment of another circle removed from its edge, so that what remains is a shape enclosed by two circular arcs of different diameters which intersect at two points .In astronomy, a crescent...
shape, is non-convex. The empty set is convex, either by definition or vacuously
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
, depending on the author.
More formally, a set Q is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1], the point
- (1 − λ) v0 + λv1
is a member of Q.
By mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, a set Q is convex if and only if every convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, . . . , vD} of a vector space is any weighted average for some indexed set of non-negative real numbers {λd} satisfying the equation = 1.
The definition of a convex set implies that the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.
Convex hull

Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s {0,1} is the closed interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s [0,1], which contains the integer end-points. The convex hull of the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
is the closed unit disk, which contains the unit circle.
Minkowski addition
In a real vector space, the Minkowski sumMinkowski addition
In geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...
of two (non-empty) sets Q1 and Q2 is defined to be the set
Sumset
In additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
Q1 + Q2 formed by the addition of vectors element-wise from the summand sets
- Q1 + Q2 = { q1 + q2 : q1 ∈ Q1 and q2 ∈ Q2 }.
For example
- {0, 1} + {0, 1} = {0+0, 0+1, 1+0, 1+1} = {0, 1, 2}.
By the principle of mathematical induction, the Minkowski sum of a finite family of (non-empty) sets
- {Qn : Qn ≠ Ø and 1 ≤ n ≤ N }
is the
set
formed by element-wise addition of vectors
- ∑ Qn = {∑ qn : qn ∈ Qn}.
Convex hulls of Minkowski sums
Minkowski addition behaves well with respect to "convexification"—the operation of taking convex hulls. Specifically, for all subsets Q1 and Q2 of a real vector space, the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of their Minkowski sum is the Minkowski sum of their convex hulls. That is,
- Conv( Q1 + Q2 ) = Conv( Q1 ) + Conv( Q2 ).
This result holds more generally, as a consequence of the principle of mathematical induction. For each finite collection of sets,
- Conv( ∑ Qn ) = ∑ Conv( Qn ).
Statements
The preceding identityConv( ∑ Qn ) = ∑ Conv( Qn )
implies that
if a point x lies in the convex hull of the Minkowski sum of N sets
- x ∈ Conv( ∑ Qn )
then x lies in the sum of the convex hulls of the summand-sets
- x ∈ ∑ Conv( Qn ).
By the definition of Minkowski addition, this last expression means that x = ∑ qn for some selection of points qn in the convex hulls of the summand-sets, that is, where each qn ∈ Conv(Qn). In this representation, the selection of the summand-points qn depends on the chosen sum-point x.
Lemma of Shapley and Folkman
.jpg)
then convexification is needed for only D summand-sets, whose choice depends on x: The point has a representation
where qd belongs to the convex hull of Qd for D (or fewer) summand-sets and qn belongs to Qn itself for the remaining sets. That is,
for some re-indexing of the summand sets; this re-indexing depends on the particular point x being represented.
The Shapley–Folkman lemma implies, for example, that every point in [0, 2] is the sum of an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
from {0, 1} and a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
from [0, 1].
Dimension of a real vector space
Conversely, the Shapley–Folkman lemma characterizes the dimensionDimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
of finite-dimensional, real vector spaces. That is, if a vector space obeys the Shapley–Folkman lemma for a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
D, and for no number less than D, then its dimension is exactly D; the Shapley–Folkman lemma holds for only finite-dimensional vector spaces.
Shapley–Folkman theorem and Starr's corollary
Shapley and Folkman used their lemma to prove their theorem, which bounds the distance between a Minkowski sum and its convex hull, the "convexified" sum:- The Shapley–Folkman theorem states that the squared Euclidean distanceEuclidean distanceIn mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
from any point in the convexified sum to the original (unconvexified) sum is bounded by the sum of the squares of the D largest circumradii of the sets Qn (the radii of the smallest spheres enclosing these setsSmallest circle problemThe smallest circle problem or minimum covering circle problem is a mathematical problem of computing the smallest circle that contains all of a given set of points in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere problem, is to compute the...
). This bound is independent of the number of summand-sets N (if
The Shapley–Folkman theorem states a bound on the distance between the Minkowski sum and its convex hull; this distance is zero if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the sum is convex. Their bound on the distance depends on the dimension D and on the shapes of the summand-sets, but not on the number of summand-sets N,
The circumradius often exceeds (and cannot be less than) the inner radius:
- The inner radius of a set Qn is defined to be the smallest number r such that, for any point q in the convex hull of Qn, there is a sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of radius r that contains a subset of Qn whose convex hull contains x.
Starr used the inner radius to reduce the upper bound stated in the Shapley–Folkman theorem:
- Starr's corollary to the Shapley–Folkman theorem states that the squared Euclidean distance from any point x in the convexified sum to the original (unconvexified) sum is bounded by the sum of the squares of the D largest inner-radii of the sets Qn.
Starr's corollary states an upper bound on the Euclidean distance between the Minkowski sum of N sets and the convex hull of the Minkowski sum; this distance between the sum and its convex hull is a measurement of the non-convexity of the set. For simplicity
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
, this distance is called the "non-convexity" of the set (with respect to Starr's measurement). Thus, Starr's bound on the non-convexity of the sum depends on only the D largest inner radii of the summand-sets; however, Starr's bound does not depend on the number of summand-sets N, when .
For example, the distance between the convex interval [0, 2] and the non-convex set {0, 1, 2} equals one-half
- 1/2 = |1 − 1/2| = |0 − 1/2| = |2 − 3/2| = |1 − 3/2|.
Thus, Starr's bound on the non-convexity of the average
- ∑ Qn
decreases as the number of summands N increases.
For example, the distance between the averaged set
- 1/2 ( {0, 1} + {0, 1} ) = {0, 1/2, 1}
and its convex hull [0, 1] is only 1/4, which is half the distance (1/2) between its summand {0, 1} and [0, 1].
The shapes of a subcollection of only D summand-sets determine the bound on the distance between the average set and its convex hull; thus, as the number of summands increases to infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, the bound decreases to zero
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
(for summand-sets of uniformly bounded size). In fact, Starr's bound on the non-convexity of this average set decreases to zero
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
as the number of summands N increases to infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
(when the inner radii of all the summands are bounded by the same number).
Proofs and computations
The original proof of the Shapley–Folkman lemma established only the existenceExistence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
of the representation, but did not provide an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for computing the representation: Similar proofs have been given by Arrow
Kenneth Arrow
Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....
and Hahn
Frank Hahn
Frank Horace Hahn is a British economist whose work has focused on general equilibrium theory, monetary theory, Keynesian economics and monetarism...
, Cassels
J. W. S. Cassels
John William Scott Cassels , FRS is a leading English mathematician.-Biography:Educated at Neville's Cross Council School in Durham and George Heriot's School in Edinburgh, Cassels graduated from the University of Edinburgh with an MA in 1943.His academic career was interrupted in World War II...
, and Schneider, among others. An abstract and elegant proof by Ekeland
Ivar Ekeland
Ivar Ekeland is a French mathematician of Norwegian descent. Ekeland has written influential monographs and textbooks on nonlinear functional analysis, the calculus of variations, and mathematical economics, as well as popular books on mathematics, which have been published in French, English, and...
has been extended by Artstein. Different proofs have appeared in unpublished papers, also. In 1981, Starr published an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for computing a representation of a given sum-point; however, his computational proof provides a weaker bound than does the original result.
Applications
The Shapley–Folkman lemma enables researchers to extend results for Minkowski sums of convex sets to sums of general sets, which need not been convex. Such sums of sets arise in economicsEconomics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, in mathematical optimization, and in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
; in each of these three mathematical sciences, non-convexity is an important feature of applications.
Economics
In economicsMicroeconomics
Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
, a consumer's preferences
Preference (economics)
In economics and other social sciences, preference refers to the set of assumptions related to ordering some alternatives, based on the degree of happiness, satisfaction, gratification, enjoyment, or utility they provide, a process which results in an optimal "choice"...
are defined over all "baskets" of goods. Each basket is represented as a non-negative vector, whose coordinates represent the quantities of the goods. On this set of baskets, an indifference curve
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
is defined for each consumer; a consumer's indifference curve contains all the baskets of commodities that the consumer regards as equivalent: That is, for every pair of baskets on the same indifference curve, the consumer does not prefer one basket over another. Through each basket of commodities passes one indifference curve. A consumer's preference set (relative to an indifference curve) is the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the indifference curve and all the commodity baskets that the consumer prefers over the indifference curve. A consumer's preferences are convex if all such preference sets are convex.
An optimal basket of goods occurs where the budget-line supports
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
a consumer's preference set, as shown in the diagram. This means that an optimal basket is on the highest possible indifference curve given the budget-line, which is defined in terms of a price vector and the consumer's income (endowment vector). Thus, the set of optimal baskets is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the prices, and this function is called the consumer's demand
Demand
- Economics :*Demand , the desire to own something and the ability to pay for it*Demand curve, a graphic representation of a demand schedule*Demand deposit, the money in checking accounts...
. If the preference set is convex, then at every price the consumer's demand is a convex set, for example, a unique optimal basket or a line-segment of baskets.
Non-convex preferences
However, if a preference set is non-convex, then some prices determine a budget-line that supports two separate optimal-baskets. For example, we can imagine that, for zoos, a lion costs as much as an eagle, and further that a zoo's budget suffices for one eagle or one lion. We can suppose also that a zoo-keeper views either animal as equally valuable. In this case, the zoo would purchase either one lion or one eagle. Of course, a contemporary zoo-keeper does not want to purchase half of an eagle and half of a lion (or a griffinGriffin
The griffin, griffon, or gryphon is a legendary creature with the body of a lion and the head and wings of an eagle...
)! Thus, the zoo-keeper's preferences are non-convex: The zoo-keeper prefers having either animal to having any strictly convex combination of both.
When the consumer's preference set is non-convex, then (for some prices) the consumer's demand is not connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
; a disconnected demand implies some discontinuous behavior by the consumer, as discussed by Harold Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...
:
If indifference curves for purchases be thought of as possessing a wavy character, convex to the origin in some regions and concave in others, we are forced to the conclusion that it is only the portions convex to the origin that can be regarded as possessing any importance, since the others are essentially unobservable. They can be detected only by the discontinuities that may occur in demand with variation in price-ratios, leading to an abrupt jumping of a point of tangency across a chasm when the straight line is rotated. But, while such discontinuities may reveal the existence of chasms, they can never measure their depth. The concave portions of the indifference curves and their many-dimensional generalizations, if they exist, must forever remain in
unmeasurable obscurity.
The difficulties of studying non-convex preferences were emphasized by Herman Wold
Herman Wold
Herman Ole Andreas Wold was a Norwegian-born econometrician and statistician who had a long career in Sweden...
and again by Paul Samuelson
Paul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
, who wrote that non-convexities are "shrouded in eternal according to Diewert.
Nonetheless, non-convex preferences were illuminated from 1959 to 1961 by a sequence of papers in The Journal of Political Economy (JPE). The main contributors were Farrell, Bator, Koopmans
Tjalling Koopmans
Tjalling Charles Koopmans was the joint winner, with Leonid Kantorovich, of the 1975 Nobel Memorial Prize in Economic Sciences....
, and Rothenberg. In particular, Rothenberg's paper discussed the approximate convexity of sums of non-convex sets. These JPE-papers stimulated a paper by Lloyd Shapley
Lloyd Shapley
Lloyd Stowell Shapley is a distinguished American mathematician and economist. He is a Professor Emeritus at University of California, Los Angeles, affiliated with departments of Mathematics and Economics...
and Martin Shubik
Martin Shubik
Martin Shubik is an American economist, who is Professor Emeritus of Mathematical Institutional Economics at Yale University. He was educated at the University of Toronto and Princeton University...
, which considered convexified consumer-preferences and introduced the concept of an "approximate equilibrium". The JPE-papers and the Shapley–Shubik paper influenced another notion of "quasi-equilibria", due to Robert Aumann
Robert Aumann
Robert John Aumann is an Israeli-American mathematician and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel...
.
Starr's 1969 paper and contemporary economics

Non-convexity (economics)
In economics, non-convexity refers to violations of the convexity assumptions of elementary economics. Basic economics textbooks concentrate on consumers with convex preferences and convex budget sets and on producers with convex production sets; for convex models, the predicted economic behavior...
were collected in an annotated bibliography by Kenneth Arrow
Kenneth Arrow
Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....
. He gave the bibliography to Starr
Ross Starr
Ross Starr is an American economist who specializes in microeconomic theory, monetary economics and mathematical economics. He is a Professor at the University of California, San Diego....
, who was then an undergraduate enrolled in Arrow's (graduate) advanced mathematical-economics course. In his term-paper, Starr studied the general equilibria of an artificial economy in which non-convex preferences were replaced by their convex hulls. In the convexified economy, at each price, the aggregate demand
Aggregate demand
In macroeconomics, aggregate demand is the total demand for final goods and services in the economy at a given time and price level. It is the amount of goods and services in the economy that will be purchased at all possible price levels. This is the demand for the gross domestic product of a...
was the sum of convex hulls of the consumers' demands. Starr's ideas interested the mathematicians Lloyd Shapley
Lloyd Shapley
Lloyd Stowell Shapley is a distinguished American mathematician and economist. He is a Professor Emeritus at University of California, Los Angeles, affiliated with departments of Mathematics and Economics...
and Jon Folkman
Jon Folkman
Jon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.-Schooling:Folkman was a Putnam Fellow in 1960. He received his Ph.D...
, who proved their eponym
Eponym
An eponym is the name of a person or thing, whether real or fictitious, after which a particular place, tribe, era, discovery, or other item is named or thought to be named...
ous lemma and theorem in "private correspondence", which was reported by Starr's published paper of 1969.
In his 1969 publication, Starr applied the Shapley–Folkman–Starr theorem. Starr proved that the "convexified" economy has general equilibria that can be closely approximated by "quasi-equilbria" of the original economy, when the number of agents exceeds the dimension of the goods: Concretely, Starr proved that there exists at least one quasi-equilibrium of prices popt with the following properties:
- For each quasi-equilibrium's prices popt, all consumers can choose optimal baskets (maximally preferred and meeting their budget constraints).
- At quasi-equilibrium prices popt in the convexified economy, every good's market is in equilibrium: Its supply equals its demand.
- For each quasi-equilibrium, the prices "nearly clear" the markets for the original economy: an upper boundUpper boundIn mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the distanceHausdorff distanceIn mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right...
between the set of equilibria of the "convexified" economy and the set of quasi-equilibria of the original economy followed from Starr's corollary to the Shapley–Folkman theorem.
Starr established that
"in the aggregate, the discrepancy between an allocation in the fictitious economy generated by [taking the convex hulls of all of the consumption and production sets] and some allocation in the real economy is bounded in a way that is independent of the number of economic agents. Therefore, the average agent experiences a deviation from intended actions that vanishes in significance as the number of agents goes to infinity".
Following Starr's 1969 paper, the Shapley–Folkman–Starr results have been widely used in economic theory. Roger Guesnerie
Roger Guesnerie
Roger Guesnerie is an economist born in France in 1943. He is currently the Chaired Professor of Economic Theory and Social Organization of the Collège de France, Director of Studies at the École des hautes études en sciences sociales, and the Chairman of the Board of Directors of the Paris School...
summarized their economic implications: "Some key results obtained under the convexity assumption remain (approximately) relevant in circumstances where convexity fails. For example, in economies with a large consumption side, preference nonconvexities do not destroy the standard results". "The derivation of these results in general form has been one of the major achievements of postwar economic theory", wrote Guesnerie. The topic of non-convex sets in economics
Non-convexity (economics)
In economics, non-convexity refers to violations of the convexity assumptions of elementary economics. Basic economics textbooks concentrate on consumers with convex preferences and convex budget sets and on producers with convex production sets; for convex models, the predicted economic behavior...
has been studied by many Nobel laureates: Arrow (1972), Robert Aumann
Robert Aumann
Robert John Aumann is an Israeli-American mathematician and a member of the United States National Academy of Sciences. He is a professor at the Center for the Study of Rationality in the Hebrew University of Jerusalem in Israel...
(2005), Gérard Debreu
Gerard Debreu
Gérard Debreu was a French economist and mathematician, who also came to have United States citizenship. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 1983 Nobel Memorial Prize in Economics.-Biography:His father was the...
(1983), Tjalling Koopmans
Tjalling Koopmans
Tjalling Charles Koopmans was the joint winner, with Leonid Kantorovich, of the 1975 Nobel Memorial Prize in Economic Sciences....
(1975), Paul Krugman
Paul Krugman
Paul Robin Krugman is an American economist, professor of Economics and International Affairs at the Woodrow Wilson School of Public and International Affairs at Princeton University, Centenary Professor at the London School of Economics, and an op-ed columnist for The New York Times...
(2008), and Paul Samuelson
Paul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
(1970); the complementary topic of convex sets in economics
Convexity in economics
Convexity is an important topic in economics. In the Arrow-Debreu model of general economic equilibrium, agents have convex budget sets and convex preferences: At equilibrium prices, the budget hyperplane supports the best attainable indifference curve. The profit function is the convex conjugate...
has been emphasized by these laureates, along with Leonid Hurwicz
Leonid Hurwicz
Leonid "Leo" Hurwicz was a Russian-born American economist and mathematician. His nationality of origin was Polish. He was Jewish. He originated incentive compatibility and mechanism design, which show how desired outcomes are achieved in economics, social science and political science...
, Leonid Kantorovich
Leonid Kantorovich
Leonid Vitaliyevich Kantorovich was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources...
(1975), and Robert Solow
Robert Solow
Robert Merton Solow is an American economist particularly known for his work on the theory of economic growth that culminated in the exogenous growth model named after him...
(1987). The Shapley–Folkman–Starr results have been featured in the economics literature: in microeconomics
Microeconomics
Microeconomics is a branch of economics that studies the behavior of how the individual modern household and firms make decisions to allocate limited resources. Typically, it applies to markets where goods or services are being bought and sold...
, in general-equilibrium theory, in public economics (including market failure
Market failure
Market failure is a concept within economic theory wherein the allocation of goods and services by a free market is not efficient. That is, there exists another conceivable outcome where a market participant may be made better-off without making someone else worse-off...
s), as well as in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, in mathematical economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
, and in applied mathematics (for economists). The Shapley–Folkman–Starr results have also influenced economics research using measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
and integration theory
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
.
Mathematical optimization
The Shapley–Folkman lemma has been used to explain why large minimizationNonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
problems with non-convexities
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
can be nearly solved (with iterative methods whose convergence proofs are stated for only convex problems).
Preliminaries of optimization theory
Nonlinear optimizationNonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
relies on the following definitions for function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s:
- The graphGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of a function f is the set of the pairs of arguments x and function evaluations f(x)
- Graph(f) = { (x, f(x) ) }
- The epigraphEpigraph (mathematics)In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....
of a real-valued functionReal-valued functionIn mathematics, a real-valued function is a function that associates to every element of the domain a real number in the image....
f is the set of points above the graph

- Epi(f) = { (x, u) : f(x) ≤ u }.
- A real-valued function is defined to be a convex functionConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
if its epigraph is a convex set.
For example, the quadratic function f(x) = x2 is convex, as is the absolute value function g(x) = |x|. However, the sine function
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
(pictured) is non-convex on the interval (0, π).
Additive optimization problems
In many optimization problems, the objective function f is separable: that is, f is the sum of many summand-functions, each of which has its own argument:- f(x) = f( (x1, ..., xN) ) = ∑ fn(xn).
For example, problems of linear optimization
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
are separable. Given a separable problem with an optimal solution, we fix an optimal solution
- xmin = (x1, ..., xN)min
with the minimum value For this separable problem, we also consider an optimal solution (xmin, f(xmin) )
to the "convexified problem", where convex hulls are taken of the graphs of the summand functions. Such an optimal solution is the limit of a sequence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of points in the convexified problem
- (xj, f(xj) ) ∈ ∑ Conv (Graph( fn ) ).
Of course, the given optimal-point is a sum of points in the graphs of the original summands and of a small number of convexified summands, by the Shapley–Folkman lemma.
This analysis was published by Ivar Ekeland
Ivar Ekeland
Ivar Ekeland is a French mathematician of Norwegian descent. Ekeland has written influential monographs and textbooks on nonlinear functional analysis, the calculus of variations, and mathematical economics, as well as popular books on mathematics, which have been published in French, English, and...
in 1974 to explain the apparent convexity of separable problems with many summands, despite the non-convexity of the summand problems. In 1973, the young mathematician Claude Lemaréchal
Claude Lemaréchal
Claude Lemaréchal is a French applied mathematician.In mathematical optimization, Claude Lemaréchal is known for his work in numerical methods for nonlinear optimization, especially for problems with nondifferentiable kinks. Lemaréchal and Phil...
was surprised by his success with convex minimization method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s on problems that were known to be non-convex; for minimizing nonlinear
Nonlinear programming
In mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
problems, a solution of the dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
problem need not provide useful information for solving the primal problem, unless the primal problem be convex and satisfy a constraint qualification. Lemaréchal's problem was additively separable, and each summand function was non-convex; nonetheless, a solution to the dual problem provided a close approximation to the primal problem's optimal value. Ekeland's analysis explained the success of methods of convex minimization on large and separable problems, despite the non-convexities of the summand functions. Ekeland and later authors argued that additive separability produced an approximately convex aggregate problem, even though the summand functions were non-convex. The crucial step in these publications is the use of the Shapley–Folkman lemma.
:
The Shapley–Folkman lemma has encouraged the use of methods of convex minimization on other applications with sums of many functions.
Probability and measure theory
Convex sets are often studied with probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. Each point in the convex hull of a (non-empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
) subset Q of a finite-dimensional space is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of a simple
Simple function
In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line which attains only a finite number of values...
random vector
Multivariate random variable
In mathematics, probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.More formally, a multivariate random...
that takes its values in Q, as a consequence of Carathéodory's lemma
Carathéodory's theorem (convex hull)
In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
. Thus, for a non-empty set Q, the collection of the expected values of the simple, Q-valued random vectors equals Q convex hull; this equality implies that the Shapley–Folkman–Starr results are useful in probability theory. In the other direction, probability theory provides tools to examine convex sets generally and the Shapley–Folkman–Starr results specifically. The Shapley–Folkman–Starr results have been widely used in the probabilistic theory of random sets
Stochastic geometry
In mathematics, stochastic geometry is the study of random spatial patterns. At the heart of the subject lies the study of random point patterns...
, for example, to prove a law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
, a central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, and a large-deviations
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
principle
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
. These proofs of probabilistic limit theorems
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
used the Shapley–Folkman–Starr results to avoid the assumption that all the random sets be convex.
A probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
is a finite measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, and the Shapley–Folkman lemma has applications in non-probabilistic measure theory, such as the theories of volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
and of vector measure
Vector measure
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
s. The Shapley–Folkman lemma enables a refinement of the Brunn–Minkowski inequality, which bounds the volume of sums in terms of the volumes of their summand-sets. The volume of a set is defined in terms of the Lebesgue measure, which is defined on subsets of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. In advanced measure-theory, the Shapley–Folkman lemma has been used to prove Lyapunov's theorem, which states that the range
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a vector measure is convex. Here, the traditional term "range" (alternatively, "image") is the set of values produced by the function. A vector measure is a vector-valued generalization of a measure; for example, if p1 and p2 are probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s defined on the same measurable space, then the product function is a vector measure,
where
is defined for every event
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
ω
by
- (p1 p2)(ω)=(p1(ω), p2(ω)).
Lyapunov's theorem has been used in economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
, in ("bang-bang") control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, and in statistical theory
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
. Lyapunov's theorem has been called a continuous
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
counterpart of the Shapley–Folkman lemma, which has itself been called a discrete analogue of Lyapunov's theorem.