Set notation
Encyclopedia
Sets are fundamental objects in mathematics
. Intuitively, a set is merely a collection of elements or members. There are various conventions for textually denoting sets. In any particular situation, an author typically chooses from among these conventions depending on which properties of the set are most relevant to the immediate context or on which perspective is most useful.
Some authors use the blackboard bold
font for these particular sets (
, 
, etc.). This usage is widely accepted in handwriting, but many mathematicians, and such experts on mathematical typography as Donald Knuth
, advise against its use in print.
of the set. Here the elements, whether expressed discretely or in some aggregate manner, are enclosed in braces.
The simplest notational approach of this type, which is feasible only for fairly small sets, is to enumerate the elements exhaustively. Thus the set of suits in a standard deck of playing cards is denoted by {♠, ♦, ♥, ♣} and the set of even prime numbers is denoted by . This approach also provides the notation for the empty set.
The semantics
of the term set imposes certain syntactic constraints on these notations. The only information that is fundamental for a set is which particular objects are, or are not, elements. As a result, the order in which elements appear in an enumeration is irrelevant: and are two enumerations of a single set. Likewise, repeated mention of an element is also irrelevant, so To deal with collections for which members' multiplicity is significant, there is a generalization of sets called multisets.
A variant of this explicitly exhaustive enumeration uses ranges of elements and features the ellipsis
. Thus the set of the first ten natural numbers is . Here, of course, the ellipsis means "and so forth." Note that wherever an ellipsis is used to denote a range, it is punctuated as though it were an element of the set. If either extreme of a range is indeterminate, it may be denoted by a mathematical expression giving a formula to compute it. As an example, if is known from context to be a positive integer, then the set of the first perfect squares
may be denoted by .
Some infinite sets, too, can be represented in this way. An example is denoting the set of natural numbers (for which one notation described above is ) by . In cases where the infinitely repeating pattern is not obvious, one can insert an expression to represent a generic element of the set, as with .
A more-powerful mechanism for denoting a set in terms of its elements is set-builder notation
. Here the general pattern is , which denotes the set of all elements (from some universal set
) for which the assertion about is true. For example, when understood as a set of points, the circle with radius and center , may be denoted as .
A notable exception to the braces notation is used to express intervals
on the real line
. Any such interval is well defined only because the real numbers are totally ordered
. It is completely determined by its left and right endpoints: the unit interval
, for instance, is the set of reals between 0 and 1. The convention for denoting intervals uses brackets and parentheses, depending as the corresponding endpoint is included in or excluded from the set, respectively. Thus the set of reals with absolute value
less than one is denoted by — note that this is very different from the ordered pair
with first entry −1 and second entry 1. As other examples, the set of reals that satisfy is denoted by , and the set of nonnegative reals is denoted by .
One class comprises those notations deriving the symbol for a set from the algebraic form of a representative element of the set. As an example, consider the set of even numbers. Since a number is even precisely if there exists some integer such that , the following variation on set-builder notation could be used to denote this set: (compare this with the formal set-builder notation: ). Alternatively, a single symbol for the set of even numbers is . Likewise, since any odd number must have the form for some integer , the set of odd numbers may be denoted .
A second class is based on a strong logical relationship between a set and a particular integer. One example is the bracket notation, in which the set of the first positive integers is denoted by (as a related point, when endowed with the standard less-than-or-equal relation
, the set yields the poset denoted by .) Another example arises from modular arithmetic
, where equivalence classes are denoted by
, which may be understood to represent the set of integers that leave remainder on division by . Thus yet another notation for the set of even numbers is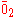 
.
Another set-denotational convention that relies on metaphor comes from enumerative combinatorics
. It derives a symbol for a set from an expression for the set's cardinality, or size, . Perhaps the simplest and best known example is the Cartesian product
of sets and , which is the set . Since in this set every element of gets paired exactly once with every element of , its cardinality is . For this reason, the set is denoted by . In fact, that same fact about its cardinality is why this set is called a product.
There are many other examples of this convention. One is the set of functions
from set to set . When and are finite, specifying any such function amounts to choosing for each element of which element of should be its image
, so the number of these functions is . Thus one denotes the set of all functions from to as . Another example is the power set of a set , which, having cardinality , is denoted by . Note, though, that since any subset
of may be seen as a function assigning to each element of one or the other element of {include, exclude}, the notation may be seen as a special case of . The cardinality metaphor has also been used to derive from the standard notation for binomial coefficients the notation
for the set of all -element subsets of a set '.
An example where this cardinality-based convention appears not to have been used yet is to denote the set of all permutations of a set . Since it is usually seen as the underlying set of a symmetric group
, this set is typically denoted by a symbol for the group itself, either or .
, one may denote the set of factors of an integer by . Similarly, a subset of is a principal lower set of a poset precisely if it can be denoted by for some in . And since is the symbol for the adjacency relation, the subset of a collection of vertices of a graph
that includes exactly those adjacent to a vertex (namely, the intersection
of with the open neighborhood
of may be denoted by .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Intuitively, a set is merely a collection of elements or members. There are various conventions for textually denoting sets. In any particular situation, an author typically chooses from among these conventions depending on which properties of the set are most relevant to the immediate context or on which perspective is most useful.
Denoting a set as an object
Where it is desirable to refer to a set as an indivisible entity, one typically denotes it by a single capital letter. In referring to an arbitrary, generic set, a typical notational choice is . When several sets are being discussed simultaneously, they are often denoted by the first few capitals: , , , and so forth. By convention, particular symbols are reserved for the most important sets of numbers:- – empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
(also
or are common) - – complex numbers
- – natural numbers
- – rational numbers (from quotientQuotientIn mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
) - – real numbers
- – integers (from zahl, German for numberNumberA number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
).
Some authors use the blackboard bold
Blackboard bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
font for these particular sets (
, , etc.). This usage is widely accepted in handwriting, but many mathematicians, and such experts on mathematical typography as Donald KnuthDonald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
, advise against its use in print.
Focusing on the membership of a set
In many contexts one is interested more in the elements that constitute the set than in the single entity comprising those elements, for instance where stating an extensional definitionExtensional definition
An extensional definition of a concept or term formulates its meaning by specifying its extension, that is, every object that falls under the definition of the concept or term in question....
of the set. Here the elements, whether expressed discretely or in some aggregate manner, are enclosed in braces.
The simplest notational approach of this type, which is feasible only for fairly small sets, is to enumerate the elements exhaustively. Thus the set of suits in a standard deck of playing cards is denoted by {♠, ♦, ♥, ♣} and the set of even prime numbers is denoted by . This approach also provides the notation for the empty set.
The semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of the term set imposes certain syntactic constraints on these notations. The only information that is fundamental for a set is which particular objects are, or are not, elements. As a result, the order in which elements appear in an enumeration is irrelevant: and are two enumerations of a single set. Likewise, repeated mention of an element is also irrelevant, so To deal with collections for which members' multiplicity is significant, there is a generalization of sets called multisets.
A variant of this explicitly exhaustive enumeration uses ranges of elements and features the ellipsis
Ellipsis
Ellipsis is a series of marks that usually indicate an intentional omission of a word, sentence or whole section from the original text being quoted. An ellipsis can also be used to indicate an unfinished thought or, at the end of a sentence, a trailing off into silence...
. Thus the set of the first ten natural numbers is . Here, of course, the ellipsis means "and so forth." Note that wherever an ellipsis is used to denote a range, it is punctuated as though it were an element of the set. If either extreme of a range is indeterminate, it may be denoted by a mathematical expression giving a formula to compute it. As an example, if is known from context to be a positive integer, then the set of the first perfect squares
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
may be denoted by .
Some infinite sets, too, can be represented in this way. An example is denoting the set of natural numbers (for which one notation described above is ) by . In cases where the infinitely repeating pattern is not obvious, one can insert an expression to represent a generic element of the set, as with .
A more-powerful mechanism for denoting a set in terms of its elements is set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
. Here the general pattern is , which denotes the set of all elements (from some universal set
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
) for which the assertion about is true. For example, when understood as a set of points, the circle with radius and center , may be denoted as .
A notable exception to the braces notation is used to express intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. Any such interval is well defined only because the real numbers are totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
. It is completely determined by its left and right endpoints: the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, for instance, is the set of reals between 0 and 1. The convention for denoting intervals uses brackets and parentheses, depending as the corresponding endpoint is included in or excluded from the set, respectively. Thus the set of reals with absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
less than one is denoted by — note that this is very different from the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
with first entry −1 and second entry 1. As other examples, the set of reals that satisfy is denoted by , and the set of nonnegative reals is denoted by .
Metaphor in denoting sets
Since so much of mathematics consists in discovering and exploiting patterns, it is perhaps not surprising that there should have arisen various set-denotational conventions that strike practitioners as obvious or natural—if sometimes only once the pattern has been pointed out.One class comprises those notations deriving the symbol for a set from the algebraic form of a representative element of the set. As an example, consider the set of even numbers. Since a number is even precisely if there exists some integer such that , the following variation on set-builder notation could be used to denote this set: (compare this with the formal set-builder notation: ). Alternatively, a single symbol for the set of even numbers is . Likewise, since any odd number must have the form for some integer , the set of odd numbers may be denoted .
A second class is based on a strong logical relationship between a set and a particular integer. One example is the bracket notation, in which the set of the first positive integers is denoted by (as a related point, when endowed with the standard less-than-or-equal relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, the set yields the poset denoted by .) Another example arises from modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, where equivalence classes are denoted by
, which may be understood to represent the set of integers that leave remainder on division by . Thus yet another notation for the set of even numbers is 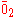.Another set-denotational convention that relies on metaphor comes from enumerative combinatorics
Enumerative combinatorics
Enumerative combinatorics is an area of combinatorics that deals with the number of ways that certain patterns can be formed. Two examples of this type of problem are counting combinations and counting permutations...
. It derives a symbol for a set from an expression for the set's cardinality, or size, . Perhaps the simplest and best known example is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of sets and , which is the set . Since in this set every element of gets paired exactly once with every element of , its cardinality is . For this reason, the set is denoted by . In fact, that same fact about its cardinality is why this set is called a product.
There are many other examples of this convention. One is the set of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from set to set . When and are finite, specifying any such function amounts to choosing for each element of which element of should be its image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
, so the number of these functions is . Thus one denotes the set of all functions from to as . Another example is the power set of a set , which, having cardinality , is denoted by . Note, though, that since any subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of may be seen as a function assigning to each element of one or the other element of {include, exclude}, the notation may be seen as a special case of . The cardinality metaphor has also been used to derive from the standard notation for binomial coefficients the notation
for the set of all -element subsets of a set '.An example where this cardinality-based convention appears not to have been used yet is to denote the set of all permutations of a set . Since it is usually seen as the underlying set of a symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, this set is typically denoted by a symbol for the group itself, either or .
Other conventions
Further conventions are also sometimes seen, including one based on relations. For a relation on a set , one may denote the set of objects related by R to some element of by . So from the notation | for the divides relation of number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, one may denote the set of factors of an integer by . Similarly, a subset of is a principal lower set of a poset precisely if it can be denoted by for some in . And since is the symbol for the adjacency relation, the subset of a collection of vertices of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
that includes exactly those adjacent to a vertex (namely, the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of with the open neighborhood
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
of may be denoted by .
See also
- List of mathematical symbols
- List (computing)
- SequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
- Set-builder notationSet-builder notationIn set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
- Mathematical notationMathematical notationMathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
- Ordinal notationOrdinal notationIn mathematical logic and set theory, an ordinal notation is a finite sequence of symbols from a finite alphabet which names an ordinal number according to some scheme which gives meaning to the language....