Semi-locally simply connected
Encyclopedia
In mathematics
, specifically algebraic topology
, the phrase semi-locally simply connected refers to a certain local connectedness
condition that arises in the theory of covering spaces. Roughly speaking, a topological space
X is semi-locally simply connected if there is a lower bound on the sizes of the “holes” in X. This condition is necessary for most of the theory of covering spaces, including the existence of a universal cover and the Galois correspondence
between covering spaces and subgroup
s of the fundamental group
.
Most “nice” spaces such as manifold
s and CW complex
es are semi-locally simply connected, and topological spaces that do not satisfy this condition are considered somewhat pathological
. The standard example of a non-semi-locally simply connected space is the Hawaiian earring
.
in X has a neighborhood
U with the property that every loop
in U can be contracted
to a single point within X (i.e. every loop is nullhomotopic). Note that the neighborhood U need not be simply connected: though every loop in U must be contractible within X, the contraction is not required to take place inside of U. For this reason, a space can be semi-locally simply connected without being locally simply connected.
Equivalent to this definition, a space X is semi-locally simply connected if every point in X has a neighborhood U for which the homomorphism
from the fundamental group
of U to the fundamental group of X, induced by the inclusion map
of U into X, is trivial.
Most of the main theorems about covering spaces, including the existence of a universal cover and the Galois correspondence, require a space to be path-connected
, locally path-connected
, and semi-locally simply connected. In particular, this condition is necessary for a space to have a simply connected covering space.
 Any “nice” space such as a manifold
Any “nice” space such as a manifold
or CW complex
is semi-locally simply connected. In some sense, only a pathological
space can fail to satisfy this condition.
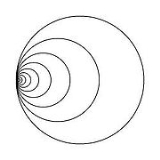
A simple example of a space that is not semi-locally simply connected is the Hawaiian earring
: the union
of the circle
s in the Euclidean plane with centers (1/n, 0) and radii
1/n, for n a natural number
. Give this space the subspace topology
. Then all neighborhoods of the origin
contain circle
s that are not nullhomotopic.
The Hawaiian earring can also be used to construct a semi-locally simply connected space that is not locally simply connected. In particular, the cone
on the Hawaiian earring is contractible and therefore semi-locally simply connected, but it is clearly not locally simply connected.
Another example of a non-semi-locally simply connected space is the complement
of Q × Q in the Euclidean plane R2, where Q denotes the set of rational number
s. In fact, the fundamental group of this space is uncountable (Hatcher p. 54).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the phrase semi-locally simply connected refers to a certain local connectedness
Locally connected space
In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
condition that arises in the theory of covering spaces. Roughly speaking, a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is semi-locally simply connected if there is a lower bound on the sizes of the “holes” in X. This condition is necessary for most of the theory of covering spaces, including the existence of a universal cover and the Galois correspondence
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between covering spaces and subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
.
Most “nice” spaces such as manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s and CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es are semi-locally simply connected, and topological spaces that do not satisfy this condition are considered somewhat pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
. The standard example of a non-semi-locally simply connected space is the Hawaiian earring
Hawaiian earring
In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
.
Definition
A space X is called semi-locally simply connected if every pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in X has a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
U with the property that every loop
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
in U can be contracted
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to a single point within X (i.e. every loop is nullhomotopic). Note that the neighborhood U need not be simply connected: though every loop in U must be contractible within X, the contraction is not required to take place inside of U. For this reason, a space can be semi-locally simply connected without being locally simply connected.
Equivalent to this definition, a space X is semi-locally simply connected if every point in X has a neighborhood U for which the homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of U to the fundamental group of X, induced by the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
of U into X, is trivial.
Most of the main theorems about covering spaces, including the existence of a universal cover and the Galois correspondence, require a space to be path-connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, locally path-connected
Locally connected space
In topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
, and semi-locally simply connected. In particular, this condition is necessary for a space to have a simply connected covering space.
Examples

Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
or CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
is semi-locally simply connected. In some sense, only a pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
space can fail to satisfy this condition.
A simple example of a space that is not semi-locally simply connected is the Hawaiian earring
Hawaiian earring
In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
: the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s in the Euclidean plane with centers (1/n, 0) and radii
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
1/n, for n a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. Give this space the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
. Then all neighborhoods of the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
contain circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s that are not nullhomotopic.
The Hawaiian earring can also be used to construct a semi-locally simply connected space that is not locally simply connected. In particular, the cone
Cone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
on the Hawaiian earring is contractible and therefore semi-locally simply connected, but it is clearly not locally simply connected.
Another example of a non-semi-locally simply connected space is the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of Q × Q in the Euclidean plane R2, where Q denotes the set of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. In fact, the fundamental group of this space is uncountable (Hatcher p. 54).

