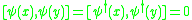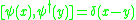Schrödinger field
Encyclopedia
In quantum mechanics
and quantum field theory
, a Schrödinger field, named after Erwin Schrödinger
, is a quantum field
which obeys the Schrödinger equation
. While any situation described by a Schrödinger field can also be described by a many-body
Schrödinger equation for identical particles, the field theory is more suitable for situations where the particle number
changes.
A Schrödinger field is also the classical limit of a quantum Schrödinger field, a classical wave which satisfies the Schrödinger equation. Unlike the quantum mechanical wavefunction, if there are interactions between the particles the equation will be nonlinear
. These nonlinear equations describe the classical wave limit of a system of interacting identical particles.
The path integral of a Schrödinger field is also known as a coherent state path integral, because the field itself is an annihilation operator whose eigenstates can be thought of as coherent states of the harmonic oscillations of the field modes.
Schrödinger fields are useful for describing Bose-Einstein condensation, the Bogolyubov
-de Gennes
equation of superconductivity
, superfluidity, and many-body theory
in general. They are also a useful alternative formalism for nonrelativistic quantum mechanics.
A Schrödinger field is the nonrelativistic limit of a Klein-Gordon field
.
whose quanta
obey the Schrödinger equation
. In the classical limit, it can be understood as the quantized wave equation of a Bose Einstein condensate or a superfluid
.
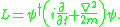
When is a complex valued field in a path integral, or equivalently an operator with canonical commutation relations, it describes a collection of identical nonrelativistic bosons. When
is a complex valued field in a path integral, or equivalently an operator with canonical commutation relations, it describes a collection of identical nonrelativistic bosons. When 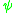 is a grassmann valued field
is a grassmann valued field
, or equivalently an operator with canonical anticommutation relations, the field describes identical fermions.
1
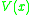 , the interaction makes a local contribution to the action:
, the interaction makes a local contribution to the action: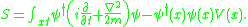
If the ordinary Schrödinger equation for V has known energy eigenstates with energies
with energies 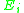 , then the field in the action can be rotated into a diagonal basis by a mode expansion:
, then the field in the action can be rotated into a diagonal basis by a mode expansion: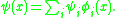
The action becomes: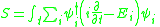
which is the position-momentum path integral for a collection of independent Harmonic oscillators.
To see the equivalence, note that decomposed into real and imaginary parts the action is:
after an integration by parts. Integrating over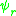 gives the action
gives the action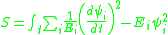
which, rescaling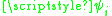 , is a harmonic oscillator action with frequency
, is a harmonic oscillator action with frequency  .
.
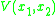 , the interaction is a nonlocal contribution to the action:
, the interaction is a nonlocal contribution to the action: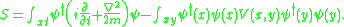
A pair-potential is the non-relativistic limit of a relativistic field coupled to electrodynamics. Ignoring the propagating degrees of freedom, the interaction between nonrelativistic electrons is the coulomb repulsion. In 3+1 dimensions, this is: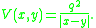
When coupled to an external potential to model classical positions of nuclei, a Schrödinger field with this pair potential describes nearly all of condensed matter physics. The exceptions are effects like superfluidity, where the quantum mechanical interference of nuclei is important, and inner shell electrons where the electron motion can be relativistic.
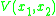 is widely studied, and is known as the nonlinear Schrödinger equation
is widely studied, and is known as the nonlinear Schrödinger equation
. Because the interactions always happen when two particles occupy the same point, the action for the nonlinear Schrödinger equation is local: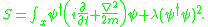
The interaction strength requires renormalization in dimensions higher than 2 and in two dimensions it has logarithmic running. In any dimensions, and even with power-law running, the theory is well defined. If the particles are fermions, the interaction vanishes.
requires renormalization in dimensions higher than 2 and in two dimensions it has logarithmic running. In any dimensions, and even with power-law running, the theory is well defined. If the particles are fermions, the interaction vanishes.
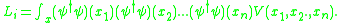
These types of potentials are important in some effective descriptions of close-packed atoms. Higher order interactions are less and less important.
 is
is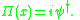
The canonical commutation relations are like an independent harmonic oscillator at each point:
The field Hamiltonian is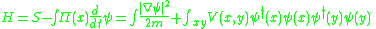
and the field equation for any interaction is a nonlinear and nonlocal version of the Schrödinger equation. For pairwise interactions: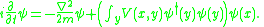
s is called many-body perturbation theory. The propagator
is
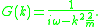
The interaction vertex is the Fourier transform of the pair-potential. In all the interactions, the number of incoming and outgoing lines is equal.
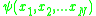 which is the probability amplitude for N particles to have the listed positions. The Schrödinger equation for
which is the probability amplitude for N particles to have the listed positions. The Schrödinger equation for  is:
is:
with Hamiltonian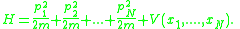
Since the particles are indistinguishable, the wavefunction has some symmetry under switching
positions. Either
Since the particles are indistinguishable, the potential V must be unchanged under permutations.
If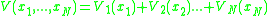
then it must be the case that . If
. If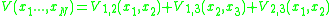
then and so on.
and so on.
In the Schrödinger equation formalism, the restrictions on the potential are ad-hoc, and the classical wave limit is hard to reach. It also has limited usefulness if a system is open to the environment, because particles might coherently enter and leave.
include configurations with arbitrary particle number. A nearly complete basis for this set of states is the collection:
labeled by the total number of particles and their position. An arbitrary state with particles at separated positions is described by a superposition of states of this form.
In this formalism, keep in mind that any two states whose positions can be permuted into each other are really the same, so the integration domains need to avoid double counting. Also keep in mind that the states with more than one particle at the same point have not yet been defined. The quantity is the amplitude that no particles are present, and its absolute square is the probability that the system is in the vacuum.
is the amplitude that no particles are present, and its absolute square is the probability that the system is in the vacuum.
In order to reproduce the Schrödinger description, the inner product on the basis states should be
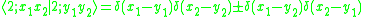
and so on. Since the discussion is nearly formally identical for bosons and fermions, although the physical properties are different, from here on the particles will be bosons.
There are natural operators in this Hilbert space. One operator, called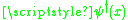 , is the operator which introduces an extra particle at x.
, is the operator which introduces an extra particle at x.
It is defined on each basis state: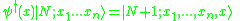
with slight ambiguity when a particle is already at x.
Another operator removes a particle at x, and is called . This operator is the conjugate of the operator
. This operator is the conjugate of the operator  . Because
. Because  has no matrix elements which connect to states with no particle at x,
has no matrix elements which connect to states with no particle at x, 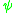 must give zero when acting on such a state.
must give zero when acting on such a state.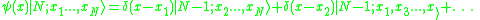
The position basis is an inconvenient way to understand coincident particles because states with a particle localized at one point have infinite energy, so intuition is difficult. In order to see what happens when two particles are at exactly the same point, it is mathematically simplest either to make space into a discrete lattice
, or to Fourier transform the field in a finite volume.
The operator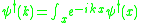
creates a superposition of one particle states in a plane wave state with momentum k, in other words, it produces a new particle with momentum k. The operator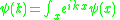
annihilates a particle with momentum k.
If the potential energy for interaction of infinitely distant particles vanishes, the fourier transformed operators in infinite volume create states which are noninteracting. The states are infinitely spread out, and the chance that the particles are nearby is zero.
The matrix elements for the operators between non-coincident points reconstructs the matrix elements of the Fourier transform between all modes:
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, a Schrödinger field, named after Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
, is a quantum field
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
which obeys the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. While any situation described by a Schrödinger field can also be described by a many-body
Many-body theory
The many-body theory is an area of physics which provides the framework for understanding the collective behavior of vast assemblies of interacting particles. In general terms, the many-body theory deals with effects that manifest themselves only in systems containing large numbers of constituents...
Schrödinger equation for identical particles, the field theory is more suitable for situations where the particle number
Particle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
changes.
A Schrödinger field is also the classical limit of a quantum Schrödinger field, a classical wave which satisfies the Schrödinger equation. Unlike the quantum mechanical wavefunction, if there are interactions between the particles the equation will be nonlinear
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
. These nonlinear equations describe the classical wave limit of a system of interacting identical particles.
The path integral of a Schrödinger field is also known as a coherent state path integral, because the field itself is an annihilation operator whose eigenstates can be thought of as coherent states of the harmonic oscillations of the field modes.
Schrödinger fields are useful for describing Bose-Einstein condensation, the Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
-de Gennes
Pierre-Gilles de Gennes
Pierre-Gilles de Gennes was a French physicist and the Nobel Prize laureate in physics in 1991.-Biography:...
equation of superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, superfluidity, and many-body theory
Many-body theory
The many-body theory is an area of physics which provides the framework for understanding the collective behavior of vast assemblies of interacting particles. In general terms, the many-body theory deals with effects that manifest themselves only in systems containing large numbers of constituents...
in general. They are also a useful alternative formalism for nonrelativistic quantum mechanics.
A Schrödinger field is the nonrelativistic limit of a Klein-Gordon field
Klein-Gordon equation
The Klein–Gordon equation is a relativistic version of the Schrödinger equation....
.
Summary
A Schrödinger field is a quantum fieldQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
whose quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
obey the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. In the classical limit, it can be understood as the quantized wave equation of a Bose Einstein condensate or a superfluid
Superfluid
Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...
.
Free field
A Schrödinger field has the free field Lagrangian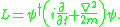
When
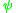 is a complex valued field in a path integral, or equivalently an operator with canonical commutation relations, it describes a collection of identical nonrelativistic bosons. When
is a complex valued field in a path integral, or equivalently an operator with canonical commutation relations, it describes a collection of identical nonrelativistic bosons. When 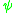 is a grassmann valued field
is a grassmann valued fieldBerezin integral
In mathematical physics, a Grassmann integral, or, more correctly, Berezin integral, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a...
, or equivalently an operator with canonical anticommutation relations, the field describes identical fermions.
1
External potential
If the particles interact with an external potential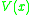 , the interaction makes a local contribution to the action:
, the interaction makes a local contribution to the action: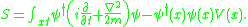
If the ordinary Schrödinger equation for V has known energy eigenstates
 with energies
with energies 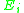 , then the field in the action can be rotated into a diagonal basis by a mode expansion:
, then the field in the action can be rotated into a diagonal basis by a mode expansion: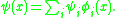
The action becomes:
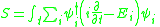
which is the position-momentum path integral for a collection of independent Harmonic oscillators.
To see the equivalence, note that decomposed into real and imaginary parts the action is:

after an integration by parts. Integrating over
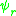 gives the action
gives the action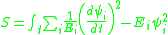
which, rescaling
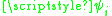 , is a harmonic oscillator action with frequency
, is a harmonic oscillator action with frequency  .
.Pair potential
When the particles interact with a pair potentialPair potential
In mechanics, a pair potential is a function that describes the potential energy of two interacting objects. Examples of pair potentials include the Coulomb's law, Newton's law of universal gravitation, the Lennard-Jones potential and the Morse potential....
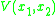 , the interaction is a nonlocal contribution to the action:
, the interaction is a nonlocal contribution to the action: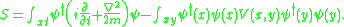
A pair-potential is the non-relativistic limit of a relativistic field coupled to electrodynamics. Ignoring the propagating degrees of freedom, the interaction between nonrelativistic electrons is the coulomb repulsion. In 3+1 dimensions, this is:
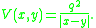
When coupled to an external potential to model classical positions of nuclei, a Schrödinger field with this pair potential describes nearly all of condensed matter physics. The exceptions are effects like superfluidity, where the quantum mechanical interference of nuclei is important, and inner shell electrons where the electron motion can be relativistic.
Nonlinear Schrödinger equation
A special case of a delta-function interaction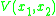 is widely studied, and is known as the nonlinear Schrödinger equation
is widely studied, and is known as the nonlinear Schrödinger equationNonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
. Because the interactions always happen when two particles occupy the same point, the action for the nonlinear Schrödinger equation is local:
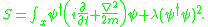
The interaction strength
 requires renormalization in dimensions higher than 2 and in two dimensions it has logarithmic running. In any dimensions, and even with power-law running, the theory is well defined. If the particles are fermions, the interaction vanishes.
requires renormalization in dimensions higher than 2 and in two dimensions it has logarithmic running. In any dimensions, and even with power-law running, the theory is well defined. If the particles are fermions, the interaction vanishes.Many-body potentials
The potentials can include many-body contributions. The interacting Lagrangian is then: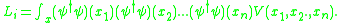
These types of potentials are important in some effective descriptions of close-packed atoms. Higher order interactions are less and less important.
Canonical formalism
The canonical momentum association with the field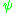 is
is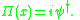
The canonical commutation relations are like an independent harmonic oscillator at each point:

The field Hamiltonian is
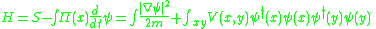
and the field equation for any interaction is a nonlinear and nonlocal version of the Schrödinger equation. For pairwise interactions:
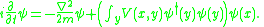
Perturbation theory
The expansion in Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s is called many-body perturbation theory. The propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
is
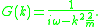
The interaction vertex is the Fourier transform of the pair-potential. In all the interactions, the number of incoming and outgoing lines is equal.
Identical particles
The many body Schrödinger equation for identical particles describes the time evolution of the many-body wavefunction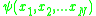 which is the probability amplitude for N particles to have the listed positions. The Schrödinger equation for
which is the probability amplitude for N particles to have the listed positions. The Schrödinger equation for  is:
is:
with Hamiltonian
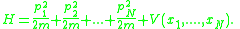
Since the particles are indistinguishable, the wavefunction has some symmetry under switching
positions. Either
 for bosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
for bosonBosonIn particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s, for fermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
for fermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s.
Since the particles are indistinguishable, the potential V must be unchanged under permutations.
If
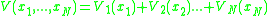
then it must be the case that
 . If
. If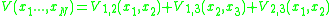
then
 and so on.
and so on.In the Schrödinger equation formalism, the restrictions on the potential are ad-hoc, and the classical wave limit is hard to reach. It also has limited usefulness if a system is open to the environment, because particles might coherently enter and leave.
Nonrelativistic Fock space
A Schrödinger field is defined by extending the Hilbert space of states toinclude configurations with arbitrary particle number. A nearly complete basis for this set of states is the collection:

labeled by the total number of particles and their position. An arbitrary state with particles at separated positions is described by a superposition of states of this form.

In this formalism, keep in mind that any two states whose positions can be permuted into each other are really the same, so the integration domains need to avoid double counting. Also keep in mind that the states with more than one particle at the same point have not yet been defined. The quantity
 is the amplitude that no particles are present, and its absolute square is the probability that the system is in the vacuum.
is the amplitude that no particles are present, and its absolute square is the probability that the system is in the vacuum.In order to reproduce the Schrödinger description, the inner product on the basis states should be

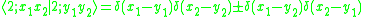
and so on. Since the discussion is nearly formally identical for bosons and fermions, although the physical properties are different, from here on the particles will be bosons.
There are natural operators in this Hilbert space. One operator, called
 , is the operator which introduces an extra particle at x.
, is the operator which introduces an extra particle at x.It is defined on each basis state:
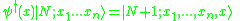
with slight ambiguity when a particle is already at x.
Another operator removes a particle at x, and is called
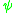 . This operator is the conjugate of the operator
. This operator is the conjugate of the operator  . Because
. Because  has no matrix elements which connect to states with no particle at x,
has no matrix elements which connect to states with no particle at x, 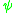 must give zero when acting on such a state.
must give zero when acting on such a state.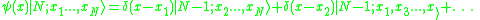
The position basis is an inconvenient way to understand coincident particles because states with a particle localized at one point have infinite energy, so intuition is difficult. In order to see what happens when two particles are at exactly the same point, it is mathematically simplest either to make space into a discrete lattice
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
, or to Fourier transform the field in a finite volume.
The operator
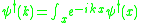
creates a superposition of one particle states in a plane wave state with momentum k, in other words, it produces a new particle with momentum k. The operator
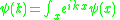
annihilates a particle with momentum k.
If the potential energy for interaction of infinitely distant particles vanishes, the fourier transformed operators in infinite volume create states which are noninteracting. The states are infinitely spread out, and the chance that the particles are nearby is zero.
The matrix elements for the operators between non-coincident points reconstructs the matrix elements of the Fourier transform between all modes:
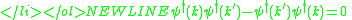
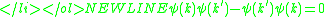
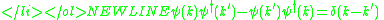
where the delta function is either the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
or the Kronecker delta, depending on whether the volume is infinite or finite.
The commutation relations now determine the operators completely, and when the spatial volume is finite, there are no conceptual hurdle to understand coinciding momenta because momenta are discrete. In a discrete momentum basis, the basis states are: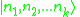
where the n's are the number of particles at each momentum. For fermions and anyons, the number of particles at any momentum is always either zero or one. The operators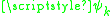 have harmonic-oscillator like matrix elements between states, independent of the interaction:
have harmonic-oscillator like matrix elements between states, independent of the interaction: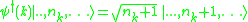
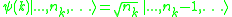
So that the operator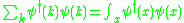
counts the total number of particles.
Now it is easy to see that the matrix elements of and
and 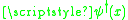 have harmonic oscillator commutation relations too.
have harmonic oscillator commutation relations too.
So that there really is no difficulty with coincident particles in position space.
The operator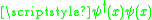 which removes and replaces a particle, acts as a sensor to detect if a particle is present at x. The operator
which removes and replaces a particle, acts as a sensor to detect if a particle is present at x. The operator  acts to multiply the state by the gradient of the many body wavefunction. The operator
acts to multiply the state by the gradient of the many body wavefunction. The operator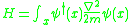
acts to reproduce the right hand side of the Schrödinger equation when acting on any basis state, so that
holds as an operator equation. Since this is true for an arbitrary state, it is also true without the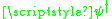 .
.
To add interactions, add nonlinear terms in the field equations. The field form automatically ensures that the potentials obey the restrictions from symmetry.
Field Hamiltonian
The field Hamiltonian which reproduces the equations of motion is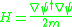
The Heisenberg equations of motion for this operator reproduces the equation of motion for the field.
To find the classical field Lagrangian, apply a Legendre transform to the classical limit of the Hamiltonian.
Although this is correct classically, the quantum mechanical transformation is not completely conceptually straightforward because the path integral is over eigenvalues of operators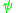 which are not hermitianHermitianA number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
which are not hermitianHermitianA number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
and whose eigenvalues are not orthogonal. The path integral over field states therefore seems naively to be overcounting. This is not the case, because the time derivative term in L includes the overlap between the different field states.