Schmidt decomposition
Encyclopedia
In linear algebra
, the Schmidt decomposition (named after its originator Erhard Schmidt
) refers to a particular way of expressing a vector
in the tensor product
of two inner product space
s. It has applications in quantum information theory and plasticity
.
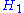and 
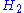be Hilbert spaces of dimension
s n and m respectively. Assume
. For any vector 
in the tensor product 
, there exist orthonormal sets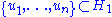 
and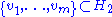 
such that 
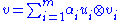, where the scalars 
are non-negative and, as a set, uniquely determined by 
.
in a different context. Fix orthonormal bases
and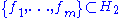 
. We can identify an elementary tensor 
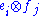with the matrix 
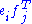, where 
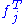is the transpose
of
. A general element of the tensor product
can then be viewed as the n × m matrix
By the singular value decomposition, there exist an n × n unitary U, m × m unitary V, and a positive semidefinite
diagonal m × m matrix Σ such that
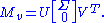
Write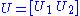
where 
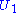is n × m and we have
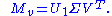
Let
be the first m column vectors of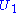 
, 
the column vectors of V, and 
the diagonal elements of Σ. The previous expression is then
which proves the claim.
Form the rank 1 matrix ρ = v v*. Then the partial trace
of ρ, with respect to either system A or B, is a diagonal matrix whose non-zero diagonal elements are |αi |2. In other words, the Schmidt decomposition shows that the reduced state of ρ on either subsystem have the same spectrum.
In the language of quantum mechanics, a rank 1 projection ρ is called a pure state. A consequence of the above comments is that, for bipartite pure states, the von Neumann entropy
of either reduced state is a well defined measure of entanglement.
the strictly positive values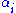
in its Schmidt decomposition are its Schmidt coefficients. The number of Schmidt coefficients of 
is called its Schmidt rank.
If w can not be expressed as
then w is said to be an entangled state
. From the Schmidt decomposition, we can see that w is entangled if and only if w has Schmidt rank strictly greater than 1. Therefore, a bipartite pure state is entangled if and only if its reduced states are mixed states.
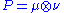. The velocity gradient is a linear combination of these across all slip systems where the scaling factor is the rate of slip along the system.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Schmidt decomposition (named after its originator Erhard Schmidt
Erhard Schmidt
Erhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
) refers to a particular way of expressing a vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
in the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of two inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
s. It has applications in quantum information theory and plasticity
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
.
Theorem
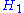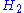Let and be Hilbert spaces of dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s n and m respectively. Assume
. For any vector in the tensor product , there exist orthonormal sets 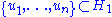and 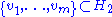such that 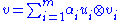, where the scalars are non-negative and, as a set, uniquely determined by .Proof
The Schmidt decomposition is essentially a restatement of the singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
in a different context. Fix orthonormal bases
and 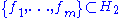. We can identify an elementary tensor 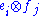with the matrix 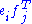, where 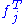is the transposeTranspose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of
. A general element of the tensor productcan then be viewed as the n × m matrix
By the singular value decomposition, there exist an n × n unitary U, m × m unitary V, and a positive semidefinite
Positive semidefinite
In mathematics, positive semidefinite may refer to:* positive-semidefinite matrix* positive-semidefinite function...
diagonal m × m matrix Σ such that
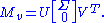
Write
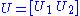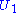where is n × m and we have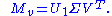Let
be the first m column vectors of 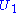, the column vectors of V, and the diagonal elements of Σ. The previous expression is thenwhich proves the claim.
Spectrum of reduced states
Consider a vector in the form of Schmidt decompositionForm the rank 1 matrix ρ = v v*. Then the partial trace
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
of ρ, with respect to either system A or B, is a diagonal matrix whose non-zero diagonal elements are |αi |2. In other words, the Schmidt decomposition shows that the reduced state of ρ on either subsystem have the same spectrum.
In the language of quantum mechanics, a rank 1 projection ρ is called a pure state. A consequence of the above comments is that, for bipartite pure states, the von Neumann entropy
Von Neumann entropy
In quantum statistical mechanics, von Neumann entropy, named after John von Neumann, is the extension of classical entropy concepts to the field of quantum mechanics....
of either reduced state is a well defined measure of entanglement.
Schmidt rank and entanglement
For an element w of the tensor productthe strictly positive values
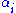in its Schmidt decomposition are its Schmidt coefficients. The number of Schmidt coefficients of is called its Schmidt rank.If w can not be expressed as
then w is said to be an entangled state
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
. From the Schmidt decomposition, we can see that w is entangled if and only if w has Schmidt rank strictly greater than 1. Therefore, a bipartite pure state is entangled if and only if its reduced states are mixed states.
Crystal plasticity
In the field of plasticity, crystalline solids such as metals deform plastically primarily along crystal planes. Each plane, defined by its normal vector ν can "slip" in one of several directions, defined by a vector μ. Together a slip plane and direction form a slip system which is described by the Schmidt tensor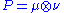. The velocity gradient is a linear combination of these across all slip systems where the scaling factor is the rate of slip along the system.