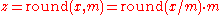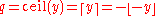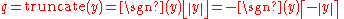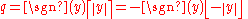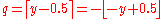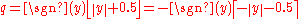Rounding
Encyclopedia
Rounding a numerical value means replacing it by another value that is approximately equal but has a shorter, simpler, or more explicit representation; for example, replacing $23.4476 with $23.45, or the fraction 312/937 with 1/3, or the expression √2 with 1.414.
Rounding is often done on purpose to obtain a value that is easier to write and handle than the original. It may be done also to indicate the accuracy of a computed number; for example, a quantity that was computed as 123,456 but is known to be accurate only to within a few hundred units is better stated as "about 123,500."
On the other hand, rounding introduces some round-off error
in the result. Rounding is almost unavoidable in many computations — especially when dividing two numbers in integer
or fixed-point arithmetic
; when computing mathematical functions such as square root
s, logarithm
s, and sine
s; or when using a floating point
representation with a fixed number of significant digits. In a sequence of calculations, these rounding errors generally accumulate, and in certain ill-conditioned cases they may make the result meaningless.
Accurate rounding of transcendental mathematical functions
is difficult because the number of extra digits that need to be calculated to resolve whether to round up or down cannot be known in advance. This problem is known as "the table-maker's dilemma".
Rounding has many similarities to the quantization
that occurs when physical quantities
must be encoded by numbers or digital signal
s.
In general, rounding a number x to a multiple of some specified increment m entails the following steps:
For example, rounding x = 2.1784 dollars to whole cents (i.e., to a multiple of 0.01) entails computing y = x/m = 2.1784/0.01 = 217.84, then rounding y to the integer q = 218, and finally computing z = q×m = 218×0.01 = 2.18.
When rounding to a predetermined number of significant digits, the increment m depends on the magnitude of the number to be rounded (or of the rounded result).
The increment m is normally a finite fraction in whatever number system
that is used to represent the numbers. For display to humans, that usually means the decimal number system (that is, m is an integer times a power of 10, like 1/1000 or 25/100). For intermediate values stored in digital computers, it often means the binary number system (m is an integer times a power of 2).
The abstract single-argument "round" function that returns an integer from an arbitrary real value has at least a dozen distinct concrete definitions presented in the rounding to integer section. The abstract two-argument "round" function is formally defined here, but in many cases it is used with the implicit value m = 1 for the increment and then reduces to the equivalent abstract single-argument function, with also the same dozen distinct concrete definitions.
There are many ways of rounding a number y to an integer q. The most common ones are
The first four methods are called directed rounding, as the displacements from the original number y to the rounded value q are all directed towards or away from the same limiting value (0, +∞
, or −∞).
If y is positive, round-down is the same as round-towards-zero, and round-up is the same as round-away-from-zero. If y is negative, round-down is the same as round-away-from-zero, and round-up is the same as round-towards-zero. In any case, if y is integer, q is just y. The following table illustrates these rounding methods:
Where many calculations are done in sequence, the choice of rounding method can have a very significant effect on the result. A famous instance involved a new index set up by the Vancouver Stock Exchange
in 1982. It was initially set at 1000.000, and after 22 months had fallen to about 520 — whereas stock prices had generally increased in the period. The problem was caused by the index being recalculated thousands of times daily, and always being rounded down to 3 decimal places, in such a way that the rounding errors accumulated. Recalculating with better rounding gave an index value of 1098.892 at the end of the same period.
For example, by this rule the value 23.5 gets rounded to 24, but −23.5 gets rounded to −23.
This is one of two rules generally taught in US elementary mathematics classes.
If it were not for the 0.5 fractions, the roundoff errors introduced by the round to nearest method would be quite symmetric: for every fraction that gets rounded up (such as 0.268), there is a complementary fraction (namely, 0.732) that gets rounded down, by the same amount. When rounding a large set of numbers with random fractional parts, these rounding errors would statistically compensate each other, and the expected (average) value of the rounded numbers would be equal to the expected value of the original numbers.
However, the round half up tie-breaking rule is not symmetric, as the fractions that are exactly 0.5 always get rounded up. This asymmetry introduces a positive bias in the roundoff errors. For example, if the fraction of y consists of three random decimal digits, then the expected value of q will be 0.0005 higher than the expected value of y. For this reason, round-to-nearest with the round half up rule is also (ambiguously) known as asymmetric rounding.
One reason for rounding up at 0.5 is that only one digit need be examined. When seeing 17.50000..., for example, the first three figures, 17.5, determines that the figure would be rounded up to 18. If the opposite rule were used (round half down), then all the zero decimal places would need to be examined to determine if the value is exactly 17.5.
For example, 23.5 gets rounded to 23, and −23.5 gets rounded to −24.
The round half down tie-breaking rule is not symmetric, as the fractions that are exactly 0.5 always get rounded down. This asymmetry introduces a negative bias in the roundoff errors. For example, if the fraction of y consists of three random decimal digits, then the expected value of q will be 0.0005 lower than the expected value of y. For this reason, round-to-nearest with the round half down rule is also (ambiguously) known as asymmetric rounding.
For example, 23.5 gets rounded to 24, and −23.5 gets rounded to −24.
This method treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. However, this rule will still introduce a positive bias for positive numbers, and a negative bias for the negative ones.
It is often used for currency conversions and price roundings (when the amount is first converted into the smallest significant subdivision of the currency, such as cents of a euro) as it is easy to explain by just considering the first fractional digit, independently of supplementary precision digits or sign of the amount (for strict equivalence between the paying and recipient of the amount).
For example, 23.5 gets rounded to 23, and −23.5 gets rounded to −23.
This method also treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. However, this rule will still introduce a negative bias for positive numbers, and a positive bias for the negative ones.
Thus, for example, +23.5 becomes +24, +22.5 becomes +22, −22.5 becomes −22, and −23.5 becomes −24.
This method also treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. In addition, for most reasonable distributions of y values, the expected (average) value of the rounded numbers is essentially the same as that of the original numbers, even if the latter are all positive (or all negative). However, this rule will still introduce a positive bias for even numbers (including zero), and a negative bias for the odd ones.
This variant of the round-to-nearest method is also called unbiased rounding, convergent rounding, statistician's rounding, Dutch rounding, Gaussian rounding, odd-even rounding or bankers' rounding. This is widely used in bookkeeping.
This is the default rounding mode used in IEEE 754 computing functions and operators.
Thus, for example, +22.5 becomes +23, +21.5 becomes +21, −21.5 becomes −21, and −22.5 becomes −23.
This method also treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. In addition, for most reasonable distributions of y values, the expected (average) value of the rounded numbers is essentially the same as that of the original numbers, even if the latter are all positive (or all negative). However, this rule will still introduce a negative bias for even numbers (including zero), and a positive bias for the odd ones.
This variant is almost never used in most computations, except in situations where one wants to avoid rounding 0.5 or −0.5 to zero, or to avoid increasing the scale of numbers represented as floating point (with limited ranges for the scaling exponent), so that a non infinite number would round to infinite, or that a small denormal value would round to a normal non-zero value (these could occur with the round half to even mode). Effectively, this mode prefers preserving the existing scale of tie numbers, avoiding out of range results when possible.
Like round-half-to-even, this rule is essentially free of overall bias; but it is also fair among even and odd q values. On the other hand, it introduces a random component into the result; performing the same computation twice on the same data may yield two different results. Also, it is open to subconscious bias if humans (rather than computers or devices of chance) are "randomly" deciding in which direction to round.
This suppresses the random component of the result, if occurrences of 0.5 fractional parts can be effectively numbered. But it can still introduce a positive or negative bias according to the direction of rounding assigned to the first occurrence, if the total number of occurrences is odd.
One way to avoid this problem is to round each value y upwards with probability equal to its fraction, and round it downwards with the complement of that probability. For example, the number 23.17 would be rounded up to 24 with probability 0.17, and down to 23 with probability 1 − 0.17 = 0.83. (This is equivalent to rounding down y + s, where s is a random number uniformly distributed between 0 and 1.) With this special rounding, known as dithering, the sudden steps get replaced by a less objectionable noise, and even small variations in the original signal will be preserved to some extent. Like the stochastic approach to tie-breaking, dithering has no bias: if all fraction values are equally likely, rounding up by a certain amount is as likely as rounding down by that same amount; and the same is true for the sum of several rounded numbers. On the other hand, dithering introduces a random component in the result, much greater than that of stochastic tie-breaking.
More precisely, the roundoff error for each dithered number will be a uniformly distributed
random variable
with mean value
zero, but with a standard deviation
 , which is better than the 1/2 standard deviation with the simple predictive methods, but slightly higher than with the simpler stochastic method. However, the sum of n rounded numbers will be a random variable with expected error zero, but with standard deviation
, which is better than the 1/2 standard deviation with the simple predictive methods, but slightly higher than with the simpler stochastic method. However, the sum of n rounded numbers will be a random variable with expected error zero, but with standard deviation 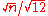 (the total remaining noise) which diverges semi-quadratically and may become easily perceptible, even if the standard deviation of the roundoff error per sample will be
(the total remaining noise) which diverges semi-quadratically and may become easily perceptible, even if the standard deviation of the roundoff error per sample will be  which slowly converges semi-quadratically to zero. So, this random distribution may still be too high for some applications that are rounding a lot of data.
which slowly converges semi-quadratically to zero. So, this random distribution may still be too high for some applications that are rounding a lot of data.
The modified values are then rounded with any one of the above rounding methods, the best ones being with stochastic or dithering methods: in this last case, the sum of n rounded numbers will still be a random variable with expected error zero but with an excellent constant standard deviation of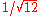 , instead of diverging semi-quadratically when dithering isolated samples; and the overall average roundoff error deviation per rounded sample will be
, instead of diverging semi-quadratically when dithering isolated samples; and the overall average roundoff error deviation per rounded sample will be 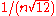 that will converge hyperbolically to zero, faster than with the semi-hyperbolic convergence when dithering isolated samples.
that will converge hyperbolically to zero, faster than with the semi-hyperbolic convergence when dithering isolated samples.
In practice, when rounding large sets of sampled data (such as audio, image and video rendering), the accumulation of roundoff errors is most frequently used with a simple predictive rounding of the modified values (such as rounding towards zero), because it will still preserve the hyperbolic convergence towards zero of the overall mean roundoff error bias and of its standard deviation. This enhancement is frequently used in image and audio processing (notably for accurate rescaling and antialiasing operations, where the simple probabilistic dithering of isolated values may still produce perceptible noise, sometimes even worse than the moiré effects
occurring with simple non-probabilistic rounding methods applied to isolated samples).
The effective propagation of accumulated roundoff errors may depend on the discrete dimension of the sampled data to round: when sampling bidimensional images, including colored images (that add the discrete dimension of color planes), or tridimensional videos (that add a discrete time dimension), or on polyphonic audio data (using time and channel discrete dimensions), it may still be preferable to propagate this error into a preferred direction, or equally into several orthogonal dimensions, such as vertically vs. horizontally for bidimensional images, or into parallel color channels at the same position and/or timestamp, and depending on other properties of these orthogonal discrete dimensions (according to a perception model). In those cases, several roundoff error accumulators may be used (at least one for each discrete dimension), or a (n-1)-dimension vector (or matrix) of accumulators.
In some of these cases, the discrete dimensions of the data to sample and round may be treated non orthogonally: for example, when working with colored images, the trichromatic color planes data in each physical dimension (height, width and optionally time) could be remapped using a perceptive color model, so that the roundoff error accumulators will be designed to preserve lightness with a higher probability than hue or saturation, instead of propagating errors into each orthogonal color plane independently; and in stereophonic audio data the two rounded data channels (left and right) may be rounded together to preserve their mean value in priority to their effective difference that will absorb most of the remaining roundoff errors, in a balanced way around zero.
whose numerator m and denominator n do not exceed a given maximum. This problem is fairly distinct from that of rounding a value to a fixed number of decimal or binary digits, or to a multiple of a given unit m. This problem is related to Farey sequence
s, the Stern-Brocot tree
, and continued fraction
s.
For example it can be used in engineering graphics for representing data with a logarithmic scale with variable steps (for example wave lengths, whose base is not necessarily an integer measure), or in statistical data to define classes of real values within intervals of exponentially growing widths (but the most common use is with integer bases such as 10 or 2).
This type of rounding is based on a logarithmic scale
defined by a fixed non-zero real scaling factor s (in most frequent cases this factor is s=1) and a fixed positive base b>1 (not necessarily an integer and most often different from the scaling factor), and a fixed integer number n>0 of significant digits in that base (which will determine the value of the increment to use for rounding, along with the computed effective scale of the rounded number).
The primary argument number (as well as the resulting rounded number) is first represented in exponential notation x = s·a·m·bc, such that the sign s is either +1 or −1, the absolute mantissa
a is restricted to the half-open positive interval [1/b,1), and the exponent c is any (positive or negative) integer. In that representation, all significant digits are in the fractional part of the absolute mantissa whose integer part is always zero.
If the source number (or rounded number) is 0, the absolute mantisssa a is defined as 0, the exponent c is fixed to an arbitrary value (0 in most conventions, but some floating-point representations can't use a null absolute mantissa but reserve a specific maximum negative value for the exponent c to represent the number 0 itself), and the sign s may be arbitrarily chosen between −1 or +1 (it is generally set to +1 for simple zero, or it is set to the same sign as the argument in the rounded value if the number representation allows to differentiate positive and negative zeroes, even if they finally represent the same numeric value 0).
A scaled exponential representation as x = a·s·bc may also be used equivalently, with a signed mantissa a either equal to zero or within one of the two half-open intervals (−1,−1/b] and [+1/b,+1), and this will be the case in the algorithm below.
The steps to compute this scaled rounding are generally similar to the following:
For the abstract "round" function, this type of rounding can use any one of the rounding to integer modes described more completely in the next section, but it is most frequently the round to nearest mode (with tie-breaking rules also described more completely below).
For example:
, writing paper, capacitors, and many other products are usually sold in only a few standard sizes.
Many design procedures describe how to calculate an approximate value, and then "round" to some standard size using phrases such as "round down to nearest standard value", "round up to nearest standard value", or "round to nearest standard value".
When a set of preferred values is equally spaced on a logarithmic scale,
Choosing the closest preferred value to any given value can be seen as a kind of scaled rounding.
Such "rounded" values can be directly calculated.
Apart from this detail, all the variants of rounding discussed above apply to the rounding of floating-point numbers as well. The algorithm for such rounding is presented in the Scaled rounding section above, but with a constant scaling factor s=1, and an integer base b>1.
For results where the rounded result would overflow the result for a directed rounding is either the appropriate signed infinity, or the highest representable positive finite number (or the lowest representable negative finite number if x is negative), depending on the direction of rounding. The result of an overflow for the usual case of round to even is always the appropriate infinity.
In addition, if the rounded result would underflow, i.e. if the exponent would exceed the lowest representable integer value, the effective result may be either zero (possibly signed if the representation can maintain a distinction of signs for zeroes), or the smallest representable positive finite number (or the highest representable negative finite number if x is negative), possibly a denormal positive or negative number (if the mantissa is storing all its significant digits, in which case the most significant digit may still be stored in a lower position by setting the highest stored digits to zero, and this stored mantissa does not drop the most significant digit, something that is possible when base b=2 because the most significant digit is always 1 in that base), depending on the direction of rounding. The result of an underflow for the usual case of round to even is always the appropriate zero.
Some computer languages and the IEEE 754-2008 standard dictate that in straightforward calculations the result should not be rounded twice. This has been a particular problem with Java as it is designed to be run identically on different machines, special programming tricks have had to be used to achieve this with x87
floating point.
The Java language was changed to allow different results where the difference does not matter and require a strictfp
qualifier to be used when the results have to conform accurately.
coined the term "The Table-Maker's Dilemma" for the unknown cost of rounding transcendental function
s:
The IEEE floating point standard guarantees that add, subtract, multiply, divide, square root, and floating point remainder will give the correctly rounded result of the infinite precision operation. However, no such guarantee is given for more complex functions and they are typically only accurate to within the last bit at best.
Using the Gelfond–Schneider theorem
and Lindemann–Weierstrass theorem
many of the standard elementary functions can be proved to return transcendental
results when given rational non-zero arguments; therefore it is always possible to correctly round such functions. However determining a limit for a given precision on how accurate results needs to be computed before a correctly rounded result can be guaranteed may demand a lot of computation time.
There are some packages around now that offer correct rounding. The GNU MPFR
package gives correctly rounded arbitrary precision results. Some other libraries implement elementary functions with correct rounding in double precision:
It is possible to devise well defined computable number
s which it may never be possible to correctly round no matter how many digits are calculated. For instance if Goldbach's conjecture
is true but unprovable then it is impossible to correctly round down 0.5 + 10-n where n is the first even number greater than 4 which is not the sum of two primes, or 0.5 if there is no such number. This can however be approximated to any given precision even if the conjecture is unprovable.
s found in Mesopotamia
contain tables with rounded values of reciprocals
and square roots in base 60.
Rounded approximations to π
, the length of the year, and the length of the month are also ancient—see base 60#Examples.
The Round-to-even method has served as the ASTM (E-29) standard since 1940. The origin of the terms unbiased rounding and statistician's rounding are fairly self-explanatory. In the 1906 4th edition of Probability and Theory of Errors Robert Simpson Woodward
called this "the computer's rule" indicating that it was then in common use by human computer
s who calculated mathematical tables. Churchill Eisenhart
's 1947 paper "Effects of Rounding or Grouping Data" (in Selected Techniques of Statistical Analysis, McGrawHill, 1947, Eisenhart, Hastay, and Wallis, editors) indicated that the practice was already "well established" in data analysis.
The origin of the term bankers' rounding remains more obscure. If this rounding method was ever a standard in banking, the evidence has proved extremely difficult to find. To the contrary, section 2 of the European Commission report The Introduction of the Euro and the Rounding of Currency Amounts suggests that there had previously been no standard approach to rounding in banking; and it specifies that "half-way" amounts should be rounded up.
Until the 1980s, the rounding method used in floating-point computer arithmetic was usually fixed by the hardware, poorly documented, inconsistent, and different for each brand and model of computer. This situation changed after the IEEE 754 floating point standard was adopted by most computer manufacturers. The standard allows the user to choose among several rounding modes, and in each case specifies precisely how the results should be rounded. These features made numerical computations more predictable and machine-independent, and made possible the efficient and consistent implementation of interval arithmetic
.
s provide functions or special syntax to round fractional numbers in various ways. The earliest numeric languages, such as FORTRAN
and C
, would provide only one method, usually truncation (towards zero). This default method could be implied in certain contexts, such as when assigning a fractional number to an integer variable
, or using a fractional number as an index of an array
. Other kinds of rounding had to be programmed explicitly; for example, rounding a positive number to the nearest integer could be implemented by adding 0.5 and truncating.
In the last decades, however, the syntax and/or the standard libraries of most languages have commonly provided at least the four basic rounding functions (up, down, to nearest, and towards zero). The tie-breaking method may vary depending the language and version, and/or may be selectable by the programmer. Several languages follow the lead of the IEEE-754 floating-point standard, and define these functions as taking a double precision float argument and returning the result of the same type, which then may be converted to an integer if necessary. Since the IEEE double precision format has 52 fraction bits, this approach may avoid spurious overflows
in languages have 32-bit integers. Some languages, such as PHP
, provide functions that round a value to a specified number of decimal digits, e.g. from 4321.5678 to 4321.57 or 4300. In addition, many languages provide a printf
or similar string formatting function, which allows one to convert a fractional number to a string, rounded to a user-specified number of decimal places (the precision). On the other hand, truncation (round to zero) is still the default rounding method used by many languages, especially for the division of two integer values.
On the opposite, CSS
and SVG
do not define any specific maximum precision for numbers and measurements, that are treated and exposed in their DOM
and in their IDL
interface as strings as if they had infinite precision, and do not discriminate between integers and floating point values; however, the implementations of these languages will typically convert these numbers into IEEE-754 double floating points before exposing the computed digits with a limited precision (notably within standard Javascript
or ECMAScript
interface bindings).
Office of the Federal Coordinator for Meteorology determined that weather data should be rounded to the nearest round number, with the "round half up" tie-breaking rule. For example, 1.5 rounded to integer should become 2, and −1.5 should become −1. Prior to that date, the tie-breaking rule was "round half away from zero".
s may write "−0" to indicate a temperature between 0.0 and −0.5 degrees (exclusive) that was rounded to integer. This notation is used when the negative sign is considered important, no matter how small is the magnitude; for example, when rounding temperatures in the Celsius
scale, where below zero indicates freezing.
Rounding is often done on purpose to obtain a value that is easier to write and handle than the original. It may be done also to indicate the accuracy of a computed number; for example, a quantity that was computed as 123,456 but is known to be accurate only to within a few hundred units is better stated as "about 123,500."
On the other hand, rounding introduces some round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
in the result. Rounding is almost unavoidable in many computations — especially when dividing two numbers in integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
or fixed-point arithmetic
Fixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
; when computing mathematical functions such as square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s, and sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
s; or when using a floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
representation with a fixed number of significant digits. In a sequence of calculations, these rounding errors generally accumulate, and in certain ill-conditioned cases they may make the result meaningless.
Accurate rounding of transcendental mathematical functions
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
is difficult because the number of extra digits that need to be calculated to resolve whether to round up or down cannot be known in advance. This problem is known as "the table-maker's dilemma".
Rounding has many similarities to the quantization
Quantization (signal processing)
Quantization, in mathematics and digital signal processing, is the process of mapping a large set of input values to a smaller set – such as rounding values to some unit of precision. A device or algorithmic function that performs quantization is called a quantizer. The error introduced by...
that occurs when physical quantities
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
must be encoded by numbers or digital signal
Digital signal
A digital signal is a physical signal that is a representation of a sequence of discrete values , for example of an arbitrary bit stream, or of a digitized analog signal...
s.
Types of rounding
Typical rounding problems are- approximating an irrational number by a fraction, e.g. πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
by 22/7; - approximating a fraction with periodic decimal expansion by a finite decimal fraction, e.g. 5/3 by 1.6667;
- replacing a rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
by a fraction with smaller numerator and denominator, e.g. 3122/9417 by 1/3; - replacing a fractional decimal number by one with fewer digits, e.g. 2.1784 dollars by 2.18 dollars;
- replacing a decimal integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
by an integer with more trailing zeros, e.g. 23,217 people by 23,200 people; or, in general, - replacing a value by a multiple of a specified amount, e.g. 27.2 seconds by 30 seconds (a multiple of 15).
Rounding to a specified increment
The most common type of rounding is to round to an integer; or, more generally, to an integer multiple of some increment — such as rounding to whole tenths of seconds, hundredths of a dollar, to whole multiples of 1/2 or 1/8 inch, to whole dozens or thousands, etc..In general, rounding a number x to a multiple of some specified increment m entails the following steps:
- Divide x by m, let the result be y;
- Round y to an integer value, call it q;
- Multiply q by m to obtain the rounded value z.
For example, rounding x = 2.1784 dollars to whole cents (i.e., to a multiple of 0.01) entails computing y = x/m = 2.1784/0.01 = 217.84, then rounding y to the integer q = 218, and finally computing z = q×m = 218×0.01 = 2.18.
When rounding to a predetermined number of significant digits, the increment m depends on the magnitude of the number to be rounded (or of the rounded result).
The increment m is normally a finite fraction in whatever number system
Number system
In mathematics, a 'number system' is a set of numbers, , together with one or more operations, such as addition or multiplication....
that is used to represent the numbers. For display to humans, that usually means the decimal number system (that is, m is an integer times a power of 10, like 1/1000 or 25/100). For intermediate values stored in digital computers, it often means the binary number system (m is an integer times a power of 2).
The abstract single-argument "round" function that returns an integer from an arbitrary real value has at least a dozen distinct concrete definitions presented in the rounding to integer section. The abstract two-argument "round" function is formally defined here, but in many cases it is used with the implicit value m = 1 for the increment and then reduces to the equivalent abstract single-argument function, with also the same dozen distinct concrete definitions.
Rounding to integer
The most basic form of rounding is to replace an arbitrary number by an integer. All the following rounding modes are concrete implementations of the abstract single-argument "round" function presented and used in the previous sections.There are many ways of rounding a number y to an integer q. The most common ones are
- round down (or take the floor, or round towards minus infinity): q is the largest integer that does not exceed y.
-
- round up (or take the ceiling, or round towards plus infinity): q is the smallest integer that is not less than y.
-
- round towards zero (or truncateTruncationIn mathematics and computer science, truncation is the term for limiting the number of digits right of the decimal point, by discarding the least significant ones.For example, consider the real numbersThe result would be:- Truncation and floor function :...
, or round away from infinity): q is the integer part of y, without its fraction digits. -
- round away from zero (or round towards infinity): if y is an integer, q is y; else q is the integer that is closest to 0 and is such that y is between 0 and q.
-
- round to nearest: q is the integer that is closest to y (see below for tie-breaking rules).
The first four methods are called directed rounding, as the displacements from the original number y to the rounded value q are all directed towards or away from the same limiting value (0, +∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
, or −∞).
If y is positive, round-down is the same as round-towards-zero, and round-up is the same as round-away-from-zero. If y is negative, round-down is the same as round-away-from-zero, and round-up is the same as round-towards-zero. In any case, if y is integer, q is just y. The following table illustrates these rounding methods:
| y | round down (towards −∞) |
round up (towards +∞) |
round towards zero |
round away from zero |
round to nearest |
|---|---|---|---|---|---|
| +23.67 | +23 | +24 | +23 | +24 | +24 |
| +23.50 | +23 | +24 | +23 | +24 | +23 or +24 |
| +23.35 | +23 | +24 | +23 | +24 | +23 |
| +23.00 | +23 | +23 | +23 | +23 | +23 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| −23.00 | −23 | −23 | −23 | −23 | −23 |
| −23.35 | −24 | −23 | −23 | −24 | −23 |
| −23.50 | −24 | −23 | −23 | −24 | −23 or −24 |
| −23.67 | −24 | −23 | −23 | −24 | −24 |
Where many calculations are done in sequence, the choice of rounding method can have a very significant effect on the result. A famous instance involved a new index set up by the Vancouver Stock Exchange
Vancouver Stock Exchange
The Vancouver Stock Exchange was a stock exchange based in Vancouver, British Columbia. It was incorporated 1906 and was the third major stock exchange in Canada, after the Toronto Stock Exchange and Montreal Stock Exchange , and featured many small-cap and exploration stocks.In 1991, it listed...
in 1982. It was initially set at 1000.000, and after 22 months had fallen to about 520 — whereas stock prices had generally increased in the period. The problem was caused by the index being recalculated thousands of times daily, and always being rounded down to 3 decimal places, in such a way that the rounding errors accumulated. Recalculating with better rounding gave an index value of 1098.892 at the end of the same period.
Tie-breaking
Rounding a number y to the nearest integer requires some tie-breaking rule for those cases when y is exactly half-way between two integers — that is, when the fraction part of y is exactly 0.5.Round half up
The following tie-breaking rule, called round half up (or round half towards plus infinity), is widely used in many disciplines. That is, half-way values y are always rounded up.- If the fraction of y is exactly 0.5, then q = y + 0.5.
-
For example, by this rule the value 23.5 gets rounded to 24, but −23.5 gets rounded to −23.
This is one of two rules generally taught in US elementary mathematics classes.
If it were not for the 0.5 fractions, the roundoff errors introduced by the round to nearest method would be quite symmetric: for every fraction that gets rounded up (such as 0.268), there is a complementary fraction (namely, 0.732) that gets rounded down, by the same amount. When rounding a large set of numbers with random fractional parts, these rounding errors would statistically compensate each other, and the expected (average) value of the rounded numbers would be equal to the expected value of the original numbers.
However, the round half up tie-breaking rule is not symmetric, as the fractions that are exactly 0.5 always get rounded up. This asymmetry introduces a positive bias in the roundoff errors. For example, if the fraction of y consists of three random decimal digits, then the expected value of q will be 0.0005 higher than the expected value of y. For this reason, round-to-nearest with the round half up rule is also (ambiguously) known as asymmetric rounding.
One reason for rounding up at 0.5 is that only one digit need be examined. When seeing 17.50000..., for example, the first three figures, 17.5, determines that the figure would be rounded up to 18. If the opposite rule were used (round half down), then all the zero decimal places would need to be examined to determine if the value is exactly 17.5.
Round half down
One may also use round half down (or round half towards minus infinity) as opposed to the more common round half up (the round half up method is a common convention, but is nothing more than a convention).- If the fraction of y is exactly 0.5, then q = y − 0.5.
-
For example, 23.5 gets rounded to 23, and −23.5 gets rounded to −24.
The round half down tie-breaking rule is not symmetric, as the fractions that are exactly 0.5 always get rounded down. This asymmetry introduces a negative bias in the roundoff errors. For example, if the fraction of y consists of three random decimal digits, then the expected value of q will be 0.0005 lower than the expected value of y. For this reason, round-to-nearest with the round half down rule is also (ambiguously) known as asymmetric rounding.
Round half away from zero
The other tie-breaking method commonly taught and used is the round half away from zero (or round half towards infinity), namely:- If the fraction of y is exactly 0.5, then q = y + 0.5 if y is positive, and q = y − 0.5 if y is negative.
-
For example, 23.5 gets rounded to 24, and −23.5 gets rounded to −24.
This method treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. However, this rule will still introduce a positive bias for positive numbers, and a negative bias for the negative ones.
It is often used for currency conversions and price roundings (when the amount is first converted into the smallest significant subdivision of the currency, such as cents of a euro) as it is easy to explain by just considering the first fractional digit, independently of supplementary precision digits or sign of the amount (for strict equivalence between the paying and recipient of the amount).
Round half towards zero
One may also round half towards zero (or round half away from infinity) as opposed to the more common round half away from zero (the round half away from zero method is a common convention, but is nothing more than a convention).- If the fraction of y is exactly 0.5, then q = y − 0.5 if y is positive, and q = y + 0.5 if y is negative.
-
For example, 23.5 gets rounded to 23, and −23.5 gets rounded to −23.
This method also treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. However, this rule will still introduce a negative bias for positive numbers, and a positive bias for the negative ones.
Round half to even
A tie-breaking rule that is even less biased is round half to even, namely- If the fraction of y is 0.5, then q is the even integer nearest to y.
Thus, for example, +23.5 becomes +24, +22.5 becomes +22, −22.5 becomes −22, and −23.5 becomes −24.
This method also treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. In addition, for most reasonable distributions of y values, the expected (average) value of the rounded numbers is essentially the same as that of the original numbers, even if the latter are all positive (or all negative). However, this rule will still introduce a positive bias for even numbers (including zero), and a negative bias for the odd ones.
This variant of the round-to-nearest method is also called unbiased rounding, convergent rounding, statistician's rounding, Dutch rounding, Gaussian rounding, odd-even rounding or bankers' rounding. This is widely used in bookkeeping.
This is the default rounding mode used in IEEE 754 computing functions and operators.
Round half to odd
Another tie-breaking rule that is very similar to round half to even, namely- If the fraction of y is 0.5, then q is the odd integer nearest to y.
Thus, for example, +22.5 becomes +23, +21.5 becomes +21, −21.5 becomes −21, and −22.5 becomes −23.
This method also treats positive and negative values symmetrically, and therefore is free of overall bias if the original numbers are positive or negative with equal probability. In addition, for most reasonable distributions of y values, the expected (average) value of the rounded numbers is essentially the same as that of the original numbers, even if the latter are all positive (or all negative). However, this rule will still introduce a negative bias for even numbers (including zero), and a positive bias for the odd ones.
This variant is almost never used in most computations, except in situations where one wants to avoid rounding 0.5 or −0.5 to zero, or to avoid increasing the scale of numbers represented as floating point (with limited ranges for the scaling exponent), so that a non infinite number would round to infinite, or that a small denormal value would round to a normal non-zero value (these could occur with the round half to even mode). Effectively, this mode prefers preserving the existing scale of tie numbers, avoiding out of range results when possible.
Stochastic rounding
Another unbiased tie-breaking method is stochastic rounding:- If the fractional part of y is .5, choose q randomly among y + 0.5 and y − 0.5, with equal probability.
Like round-half-to-even, this rule is essentially free of overall bias; but it is also fair among even and odd q values. On the other hand, it introduces a random component into the result; performing the same computation twice on the same data may yield two different results. Also, it is open to subconscious bias if humans (rather than computers or devices of chance) are "randomly" deciding in which direction to round.
Alternating tie-breaking
One method, more obscure than most, is round half alternatingly.- If the fractional part is 0.5, alternate round up and round down: for the first occurrence of a 0.5 fractional part, round up; for the second occurrence, round down; so on so forth.
This suppresses the random component of the result, if occurrences of 0.5 fractional parts can be effectively numbered. But it can still introduce a positive or negative bias according to the direction of rounding assigned to the first occurrence, if the total number of occurrences is odd.
Simple dithering
In some contexts, all the rounding methods above may be unsatisfactory. For example, suppose that y is an accurate measurement of an audio signal, which is being rounded to an integer q in order to reduce the storage or transmission costs. If y changes slowly with time, any of the rounding method above will result in q being completely constant for long intervals, separated by sudden jumps of ±1. When the q signal is played back, these steps will be heard as a very disagreeable noise, and any variations of the original signal between two integer values will be completely lost.One way to avoid this problem is to round each value y upwards with probability equal to its fraction, and round it downwards with the complement of that probability. For example, the number 23.17 would be rounded up to 24 with probability 0.17, and down to 23 with probability 1 − 0.17 = 0.83. (This is equivalent to rounding down y + s, where s is a random number uniformly distributed between 0 and 1.) With this special rounding, known as dithering, the sudden steps get replaced by a less objectionable noise, and even small variations in the original signal will be preserved to some extent. Like the stochastic approach to tie-breaking, dithering has no bias: if all fraction values are equally likely, rounding up by a certain amount is as likely as rounding down by that same amount; and the same is true for the sum of several rounded numbers. On the other hand, dithering introduces a random component in the result, much greater than that of stochastic tie-breaking.
More precisely, the roundoff error for each dithered number will be a uniformly distributed
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with mean value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
zero, but with a standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
 , which is better than the 1/2 standard deviation with the simple predictive methods, but slightly higher than with the simpler stochastic method. However, the sum of n rounded numbers will be a random variable with expected error zero, but with standard deviation
, which is better than the 1/2 standard deviation with the simple predictive methods, but slightly higher than with the simpler stochastic method. However, the sum of n rounded numbers will be a random variable with expected error zero, but with standard deviation 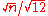 (the total remaining noise) which diverges semi-quadratically and may become easily perceptible, even if the standard deviation of the roundoff error per sample will be
(the total remaining noise) which diverges semi-quadratically and may become easily perceptible, even if the standard deviation of the roundoff error per sample will be  which slowly converges semi-quadratically to zero. So, this random distribution may still be too high for some applications that are rounding a lot of data.
which slowly converges semi-quadratically to zero. So, this random distribution may still be too high for some applications that are rounding a lot of data.Multidimensional dithering
This variant of the simple dithering method still rounds values with probability equal to its fraction. However, instead of using a random distribution for rounding isolated samples, the roundoff error occurring at each rounded sample is accumulated for the next surrounding elements to sample or compute; this accumulated value is then added to the value of these next sampled or computed values to round, so that the modified values will take into account this difference using a predictive model (such as Floyd–Steinberg dithering).The modified values are then rounded with any one of the above rounding methods, the best ones being with stochastic or dithering methods: in this last case, the sum of n rounded numbers will still be a random variable with expected error zero but with an excellent constant standard deviation of
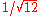 , instead of diverging semi-quadratically when dithering isolated samples; and the overall average roundoff error deviation per rounded sample will be
, instead of diverging semi-quadratically when dithering isolated samples; and the overall average roundoff error deviation per rounded sample will be 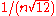 that will converge hyperbolically to zero, faster than with the semi-hyperbolic convergence when dithering isolated samples.
that will converge hyperbolically to zero, faster than with the semi-hyperbolic convergence when dithering isolated samples.In practice, when rounding large sets of sampled data (such as audio, image and video rendering), the accumulation of roundoff errors is most frequently used with a simple predictive rounding of the modified values (such as rounding towards zero), because it will still preserve the hyperbolic convergence towards zero of the overall mean roundoff error bias and of its standard deviation. This enhancement is frequently used in image and audio processing (notably for accurate rescaling and antialiasing operations, where the simple probabilistic dithering of isolated values may still produce perceptible noise, sometimes even worse than the moiré effects
Moiré pattern
In physics, a moiré pattern is an interference pattern created, for example, when two grids are overlaid at an angle, or when they have slightly different mesh sizes.- Etymology :...
occurring with simple non-probabilistic rounding methods applied to isolated samples).
The effective propagation of accumulated roundoff errors may depend on the discrete dimension of the sampled data to round: when sampling bidimensional images, including colored images (that add the discrete dimension of color planes), or tridimensional videos (that add a discrete time dimension), or on polyphonic audio data (using time and channel discrete dimensions), it may still be preferable to propagate this error into a preferred direction, or equally into several orthogonal dimensions, such as vertically vs. horizontally for bidimensional images, or into parallel color channels at the same position and/or timestamp, and depending on other properties of these orthogonal discrete dimensions (according to a perception model). In those cases, several roundoff error accumulators may be used (at least one for each discrete dimension), or a (n-1)-dimension vector (or matrix) of accumulators.
In some of these cases, the discrete dimensions of the data to sample and round may be treated non orthogonally: for example, when working with colored images, the trichromatic color planes data in each physical dimension (height, width and optionally time) could be remapped using a perceptive color model, so that the roundoff error accumulators will be designed to preserve lightness with a higher probability than hue or saturation, instead of propagating errors into each orthogonal color plane independently; and in stereophonic audio data the two rounded data channels (left and right) may be rounded together to preserve their mean value in priority to their effective difference that will absorb most of the remaining roundoff errors, in a balanced way around zero.
Rounding to simple fractions
In some contexts it is desirable to round a given number x to a "neat" fraction — that is, the nearest fraction z = m/nwhose numerator m and denominator n do not exceed a given maximum. This problem is fairly distinct from that of rounding a value to a fixed number of decimal or binary digits, or to a multiple of a given unit m. This problem is related to Farey sequence
Farey sequence
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size....
s, the Stern-Brocot tree
Stern-Brocot tree
In number theory, the Stern–Brocot tree is an infinite complete binary tree in which the vertices correspond precisely to the positive rational numbers, whose values are ordered from left to right as in a search tree....
, and continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s.
Scaled rounding
This type of rounding, which is also named rounding to a logarithmic scale, is a variant of Rounding to a specified increment but with an increment that is modified depending on the scale and magnitude of the result. Concretely, the intent is to limit the number of significant digits, rounding the value so that non-significant digits will be dropped. This type of rounding occurs implicitly with numbers computed with floating-point values with limited precision (such as IEEE-754 float and double types), but it may be used more generally to round any real values with any positive number of significant digits and any strictly positive real base.For example it can be used in engineering graphics for representing data with a logarithmic scale with variable steps (for example wave lengths, whose base is not necessarily an integer measure), or in statistical data to define classes of real values within intervals of exponentially growing widths (but the most common use is with integer bases such as 10 or 2).
This type of rounding is based on a logarithmic scale
Logarithmic scale
A logarithmic scale is a scale of measurement using the logarithm of a physical quantity instead of the quantity itself.A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4...
defined by a fixed non-zero real scaling factor s (in most frequent cases this factor is s=1) and a fixed positive base b>1 (not necessarily an integer and most often different from the scaling factor), and a fixed integer number n>0 of significant digits in that base (which will determine the value of the increment to use for rounding, along with the computed effective scale of the rounded number).
The primary argument number (as well as the resulting rounded number) is first represented in exponential notation x = s·a·m·bc, such that the sign s is either +1 or −1, the absolute mantissa
Mantissa
* The mantissa is the significand in a common logarithm or floating-point number.* Metaphorically, it is the part of the self that eludes conscious awareness or self-understanding.* An addition of little importance.Mantissa may also refer to:...
a is restricted to the half-open positive interval [1/b,1), and the exponent c is any (positive or negative) integer. In that representation, all significant digits are in the fractional part of the absolute mantissa whose integer part is always zero.
If the source number (or rounded number) is 0, the absolute mantisssa a is defined as 0, the exponent c is fixed to an arbitrary value (0 in most conventions, but some floating-point representations can't use a null absolute mantissa but reserve a specific maximum negative value for the exponent c to represent the number 0 itself), and the sign s may be arbitrarily chosen between −1 or +1 (it is generally set to +1 for simple zero, or it is set to the same sign as the argument in the rounded value if the number representation allows to differentiate positive and negative zeroes, even if they finally represent the same numeric value 0).
A scaled exponential representation as x = a·s·bc may also be used equivalently, with a signed mantissa a either equal to zero or within one of the two half-open intervals (−1,−1/b] and [+1/b,+1), and this will be the case in the algorithm below.
The steps to compute this scaled rounding are generally similar to the following:
- if x equals zero, simply return x; otherwise:
- convert x into the scaled exponential representation, with a signed mantissa:

- let x’ be the unscaled value of x, by dividing it by the scaling factor s:
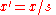 ;
; - let the scaling exponent c be one plus the base-b logarithm of the absolute value of x’, rounded down to an integer (towards minus infinity):
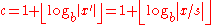 ;
; - let the signed mantissa a be product of x’ divided by b to the power c:

- let x’ be the unscaled value of x, by dividing it by the scaling factor s:
- compute the rounded value in this representation:
- let c’ be the initial scaling exponent c of x’:

- let m be the increment for rounding the mantissa a according to the number of significant digits to keep:
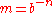
- let a’ be the signed mantissa a rounded according to this increment m and the selected rounding mode:

- if the absolute value of a’ is not lower than b, then decrement n (multiply the increment m by b), increment the scaling exponent c’, divide the signed mantissa a by b, and restart the rounding of the new signed mantissa a into a’ with the same formula; this step may be avoided only if the abtract "round" function is always rounding a towards 0 (i.e. when it is a simple truncation), but is necessary if it may be rounding a towards infinity, because the rounded mantissa may have a higher scaling exponent in this case, leaving an extra digit of precision.
- let c’ be the initial scaling exponent c of x’:
- return the rounded value:
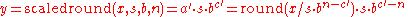 .
.
For the abstract "round" function, this type of rounding can use any one of the rounding to integer modes described more completely in the next section, but it is most frequently the round to nearest mode (with tie-breaking rules also described more completely below).
For example:
- the scaled rounding of 1.234 with scaling factor 1 in base 10 and 3 significant digits (maximum relative precision=1/1000), when using any round to nearest mode, will return 1.23;
- similar scaled rounding of 1.236 will return 1.24;
- similar scaled rounding of 21.236 will return 21.2;
- similar scaled rounding of 321.236 will return 321;
- the scaled rounding of 1.234 scaling factor 1 in base 10 and 3 significant digits (maximum relative precision=1/1000), when using the round down mode, will return 1.23;
- similar scaled rounding of 1.236 will also return 1.23;
- the scaled rounding of
 with scaling factor
with scaling factor  in base 2 and 3 significant digits (maximum relative precision=1/8), when using the round down mode, will return
in base 2 and 3 significant digits (maximum relative precision=1/8), when using the round down mode, will return  ;
; - similar scaled rounding of
 will return
will return 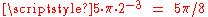 ;
; - similar scaled rounding of
 will return
will return  .
. - similar scaled rounding of
 will also return
will also return  .
. - similar scaled rounding of
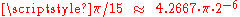 will return
will return  .
.
Round to available value
Finished lumberLumber
Lumber or timber is wood in any of its stages from felling through readiness for use as structural material for construction, or wood pulp for paper production....
, writing paper, capacitors, and many other products are usually sold in only a few standard sizes.
Many design procedures describe how to calculate an approximate value, and then "round" to some standard size using phrases such as "round down to nearest standard value", "round up to nearest standard value", or "round to nearest standard value".
When a set of preferred values is equally spaced on a logarithmic scale,
Choosing the closest preferred value to any given value can be seen as a kind of scaled rounding.
Such "rounded" values can be directly calculated.
Floating-point rounding
In floating-point arithmetic, rounding aims to turn a given value x into a value z with a specified number of significant digits. In other words, z should be a multiple of a number m that depends on the magnitude of z. The number m is a power of the base (usually 2 or 10) of the floating-point representation.Apart from this detail, all the variants of rounding discussed above apply to the rounding of floating-point numbers as well. The algorithm for such rounding is presented in the Scaled rounding section above, but with a constant scaling factor s=1, and an integer base b>1.
For results where the rounded result would overflow the result for a directed rounding is either the appropriate signed infinity, or the highest representable positive finite number (or the lowest representable negative finite number if x is negative), depending on the direction of rounding. The result of an overflow for the usual case of round to even is always the appropriate infinity.
In addition, if the rounded result would underflow, i.e. if the exponent would exceed the lowest representable integer value, the effective result may be either zero (possibly signed if the representation can maintain a distinction of signs for zeroes), or the smallest representable positive finite number (or the highest representable negative finite number if x is negative), possibly a denormal positive or negative number (if the mantissa is storing all its significant digits, in which case the most significant digit may still be stored in a lower position by setting the highest stored digits to zero, and this stored mantissa does not drop the most significant digit, something that is possible when base b=2 because the most significant digit is always 1 in that base), depending on the direction of rounding. The result of an underflow for the usual case of round to even is always the appropriate zero.
Double rounding
Rounding a number twice in succession to different precisions, with the latter precision being coarser, is not guaranteed to give the same result as rounding once to the final precision except in the case of directed rounding. For instance rounding 9.46 to one decimal gives 9.5, and then 10 when rounding to integer using rounding half to even, but would give 9 when rounded to integer directly.Some computer languages and the IEEE 754-2008 standard dictate that in straightforward calculations the result should not be rounded twice. This has been a particular problem with Java as it is designed to be run identically on different machines, special programming tricks have had to be used to achieve this with x87
X87
x87 is a floating point-related subset of the x86 architecture instruction set. It originated as an extension of the 8086 instruction set in the form of optional floating point coprocessors that worked in tandem with corresponding x86 CPUs. These microchips had names ending in "87"...
floating point.
The Java language was changed to allow different results where the difference does not matter and require a strictfp
Strictfp
strictfp is a keyword in the Java programming language that restricts floating-point calculations to ensure portability. It was introduced into Java with the Java virtual machine version 1.2.-Basis:...
qualifier to be used when the results have to conform accurately.
Exact computation with rounded arithmetic
It is possible to use rounded arithmetic to evaluate the exact value of a function with a discrete domain and range. For example, if we know that an integer n is a perfect square, we can compute its square root by converting n to a floating-point value x, computing the approximate square root y of x with floating point, and then rounding y to the nearest integer q. If n is not too big, the floating-point roundoff error in y will be less than 0.5, so the rounded value q will be the exact square root of n. In most modern computers, this method may be much faster than computing the square root of n by an all-integer algorithm.The table-maker's dilemma
William KahanWilliam Kahan
William Morton Kahan is a mathematician and computer scientist who received the Turing Award in 1989 for "his fundamental contributions to numerical analysis", and was named an ACM Fellow in 1994....
coined the term "The Table-Maker's Dilemma" for the unknown cost of rounding transcendental function
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s:
"Nobody knows how much it would cost to compute y^w correctly rounded for every two floating-point arguments at which it does not over/underflow. Instead, reputable math libraries compute elementary transcendental functions mostly within slightly more than half an ulpUnit in the Last PlaceIn computer science and numerical analysis, unit in the last place or unit of least precision is the spacing between floating-point numbers, i.e., the value the least significant bit represents if it is 1...
and almost always well within one ulp. Why can't Y^W be rounded within half an ulp like SQRT? Because nobody knows how much computation it would cost... No general way exists to predict how many extra digits will have to be carried to compute a transcendental expression and round it correctly to some preassigned number of digits. Even the fact (if true) that a finite number of extra digits will ultimately suffice may be a deep theorem."
The IEEE floating point standard guarantees that add, subtract, multiply, divide, square root, and floating point remainder will give the correctly rounded result of the infinite precision operation. However, no such guarantee is given for more complex functions and they are typically only accurate to within the last bit at best.
Using the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
and Lindemann–Weierstrass theorem
Lindemann–Weierstrass theorem
In mathematics, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if 1, ..., are algebraic numbers which are linearly independent over the rational numbers ', then 1, ..., are algebraically...
many of the standard elementary functions can be proved to return transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
results when given rational non-zero arguments; therefore it is always possible to correctly round such functions. However determining a limit for a given precision on how accurate results needs to be computed before a correctly rounded result can be guaranteed may demand a lot of computation time.
There are some packages around now that offer correct rounding. The GNU MPFR
MPFR
GNU MPFR is a portable C library for arbitrary-precision binary floating-point computation with correct rounding, based on GNU Multi-Precision Library. The computation is both efficient and has a well-defined semantics. It copies the ideas from the ANSI/IEEE-754 standard for fixed-precision...
package gives correctly rounded arbitrary precision results. Some other libraries implement elementary functions with correct rounding in double precision:
- IBMIBMInternational Business Machines Corporation or IBM is an American multinational technology and consulting corporation headquartered in Armonk, New York, United States. IBM manufactures and sells computer hardware and software, and it offers infrastructure, hosting and consulting services in areas...
's libultim, in rounding to nearest only. - Sun MicrosystemsSun MicrosystemsSun Microsystems, Inc. was a company that sold :computers, computer components, :computer software, and :information technology services. Sun was founded on February 24, 1982...
's libmcr, in the 4 rounding modes. - CRlibm, written in the Arénaire team (LIP, ENS Lyon). It supports the 4 rounding modes and is proved.
It is possible to devise well defined computable number
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
s which it may never be possible to correctly round no matter how many digits are calculated. For instance if Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
is true but unprovable then it is impossible to correctly round down 0.5 + 10-n where n is the first even number greater than 4 which is not the sum of two primes, or 0.5 if there is no such number. This can however be approximated to any given precision even if the conjecture is unprovable.
History
The concept of rounding is very old, perhaps older even than the concept of division. Some ancient clay tabletClay tablet
In the Ancient Near East, clay tablets were used as a writing medium, especially for writing in cuneiform, throughout the Bronze Age and well into the Iron Age....
s found in Mesopotamia
Mesopotamia
Mesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...
contain tables with rounded values of reciprocals
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
and square roots in base 60.
Rounded approximations to π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, the length of the year, and the length of the month are also ancient—see base 60#Examples.
The Round-to-even method has served as the ASTM (E-29) standard since 1940. The origin of the terms unbiased rounding and statistician's rounding are fairly self-explanatory. In the 1906 4th edition of Probability and Theory of Errors Robert Simpson Woodward
Robert Simpson Woodward
Robert Simpson Woodward was an American physicist and mathematician, born at Rochester, Michigan. He graduated C.E. at the University of Michigan in 1872 and was appointed assistant engineer on the United States Lake Survey. In 1882 he became assistant astronomer for the United States Transit of...
called this "the computer's rule" indicating that it was then in common use by human computer
Human computer
The term "computer", in use from the mid 17th century, meant "one who computes": a person performing mathematical calculations, before electronic computers became commercially available....
s who calculated mathematical tables. Churchill Eisenhart
Churchill Eisenhart
Dr. Churchill Eisenhart was a United States mathematician. He was Chief of the Statistical Engineering Laboratory , Applied Mathematics Division of the National Bureau of Standards ....
's 1947 paper "Effects of Rounding or Grouping Data" (in Selected Techniques of Statistical Analysis, McGrawHill, 1947, Eisenhart, Hastay, and Wallis, editors) indicated that the practice was already "well established" in data analysis.
The origin of the term bankers' rounding remains more obscure. If this rounding method was ever a standard in banking, the evidence has proved extremely difficult to find. To the contrary, section 2 of the European Commission report The Introduction of the Euro and the Rounding of Currency Amounts suggests that there had previously been no standard approach to rounding in banking; and it specifies that "half-way" amounts should be rounded up.
Until the 1980s, the rounding method used in floating-point computer arithmetic was usually fixed by the hardware, poorly documented, inconsistent, and different for each brand and model of computer. This situation changed after the IEEE 754 floating point standard was adopted by most computer manufacturers. The standard allows the user to choose among several rounding modes, and in each case specifies precisely how the results should be rounded. These features made numerical computations more predictable and machine-independent, and made possible the efficient and consistent implementation of interval arithmetic
Interval arithmetic
Interval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
.
Rounding functions in programming languages
Most programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s provide functions or special syntax to round fractional numbers in various ways. The earliest numeric languages, such as FORTRAN
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
and C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, would provide only one method, usually truncation (towards zero). This default method could be implied in certain contexts, such as when assigning a fractional number to an integer variable
Variable (programming)
In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
, or using a fractional number as an index of an array
Array data type
In computer science, an array type is a data type that is meant to describe a collection of elements , each selected by one or more indices that can be computed at run time by the program. Such a collection is usually called an array variable, array value, or simply array...
. Other kinds of rounding had to be programmed explicitly; for example, rounding a positive number to the nearest integer could be implemented by adding 0.5 and truncating.
In the last decades, however, the syntax and/or the standard libraries of most languages have commonly provided at least the four basic rounding functions (up, down, to nearest, and towards zero). The tie-breaking method may vary depending the language and version, and/or may be selectable by the programmer. Several languages follow the lead of the IEEE-754 floating-point standard, and define these functions as taking a double precision float argument and returning the result of the same type, which then may be converted to an integer if necessary. Since the IEEE double precision format has 52 fraction bits, this approach may avoid spurious overflows
Arithmetic overflow
The term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
in languages have 32-bit integers. Some languages, such as PHP
PHP
PHP is a general-purpose server-side scripting language originally designed for web development to produce dynamic web pages. For this purpose, PHP code is embedded into the HTML source document and interpreted by a web server with a PHP processor module, which generates the web page document...
, provide functions that round a value to a specified number of decimal digits, e.g. from 4321.5678 to 4321.57 or 4300. In addition, many languages provide a printf
Printf
Printf format string refers to a control parameter used by a class of functions typically associated with some types of programming languages. The format string specifies a method for rendering an arbitrary number of varied data type parameter into a string...
or similar string formatting function, which allows one to convert a fractional number to a string, rounded to a user-specified number of decimal places (the precision). On the other hand, truncation (round to zero) is still the default rounding method used by many languages, especially for the division of two integer values.
On the opposite, CSS
Cascading Style Sheets
Cascading Style Sheets is a style sheet language used to describe the presentation semantics of a document written in a markup language...
and SVG
Scalable Vector Graphics
Scalable Vector Graphics is a family of specifications of an XML-based file format for describing two-dimensional vector graphics, both static and dynamic . The SVG specification is an open standard that has been under development by the World Wide Web Consortium since 1999.SVG images and their...
do not define any specific maximum precision for numbers and measurements, that are treated and exposed in their DOM
Document Object Model
The Document Object Model is a cross-platform and language-independent convention for representing and interacting with objects in HTML, XHTML and XML documents. Aspects of the DOM may be addressed and manipulated within the syntax of the programming language in use...
and in their IDL
Interface description language
An interface description language , or IDL for short, is a specification language used to describe a software component's interface...
interface as strings as if they had infinite precision, and do not discriminate between integers and floating point values; however, the implementations of these languages will typically convert these numbers into IEEE-754 double floating points before exposing the computed digits with a limited precision (notably within standard Javascript
JavaScript
JavaScript is a prototype-based scripting language that is dynamic, weakly typed and has first-class functions. It is a multi-paradigm language, supporting object-oriented, imperative, and functional programming styles....
or ECMAScript
ECMAScript
ECMAScript is the scripting language standardized by Ecma International in the ECMA-262 specification and ISO/IEC 16262. The language is widely used for client-side scripting on the web, in the form of several well-known dialects such as JavaScript, JScript, and ActionScript.- History :JavaScript...
interface bindings).
Other rounding standards
Some disciplines or institutions have issued standards or directives for rounding.U.S. Weather Observations
In a guideline issued in mid-1966, the U.S.United States
The United States of America is a federal constitutional republic comprising fifty states and a federal district...
Office of the Federal Coordinator for Meteorology determined that weather data should be rounded to the nearest round number, with the "round half up" tie-breaking rule. For example, 1.5 rounded to integer should become 2, and −1.5 should become −1. Prior to that date, the tie-breaking rule was "round half away from zero".
Negative zero in meteorology
Some meteorologistMeteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
s may write "−0" to indicate a temperature between 0.0 and −0.5 degrees (exclusive) that was rounded to integer. This notation is used when the negative sign is considered important, no matter how small is the magnitude; for example, when rounding temperatures in the Celsius
Celsius
Celsius is a scale and unit of measurement for temperature. It is named after the Swedish astronomer Anders Celsius , who developed a similar temperature scale two years before his death...
scale, where below zero indicates freezing.
See also
- False precisionFalse precisionFalse precision occurs when numerical data are presented in a manner that implies better precision than is actually the case; since precision is a limit to accuracy, this often leads to overconfidence in the accuracy as well.In science and engineering, convention dictates that...
- Gal's accurate tablesGal's accurate tablesGal's accurate tables is a method devised by Shmuel Gal to provide accurate values of special functions using a lookup table and interpolation. It is a fast and efficient method for generating values of functions like the exponential or the trigonometric functions to within last-bit accuracy for...
- Interval arithmeticInterval arithmeticInterval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
- Kahan summation algorithmKahan summation algorithmIn numerical analysis, the Kahan summation algorithm significantly reduces the numerical error in the total obtained by adding a sequence of finite precision floating point numbers, compared to the obvious approach...
- Nearest integer functionNearest integer functionIn computer science, the nearest integer function of real number x denoted variously by [x], \lfloor x \rceil, \Vert x \Vert, nint, or Round, is a function which returns the nearest integer to x. To avoid ambiguity when operating on half-integers, a rounding rule must be chosen...
- Round-off errorRound-off errorA round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
- Significant figuresSignificant figuresThe significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:...
- TruncationTruncationIn mathematics and computer science, truncation is the term for limiting the number of digits right of the decimal point, by discarding the least significant ones.For example, consider the real numbersThe result would be:- Truncation and floor function :...
- Signed zero
- Swedish roundingSwedish roundingSwedish rounding is rounding the basic cost of a purchase which is to be paid for in cash to the nearest multiple of the smallest denomination of currency...
, to avoid the use of coins of extremely low value
External links
- An introduction to different rounding algorithms that is accessible to a general audience but especially useful to those studying computer science and electronics.
- A complete treatment of mathematical rounding. by John Kennedy
- How To Implement Custom Rounding Procedures by Microsoft