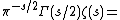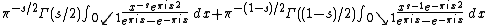Riemann–Siegel formula
Encyclopedia
In mathematics, the Riemann–Siegel formula is an asymptotic formula for the error of the approximate functional equation of the Riemann zeta function, an approximation of the zeta function by a sum of two finite Dirichlet series. It was found by in unpublished manuscripts of Bernhard Riemann
dating from the 1850s. Siegel derived it from the Riemann–Siegel integral formula, an expression for the zeta function involving contour integrals. It is often used to compute values of the Riemann–Siegel formula, sometimes in combination with the Odlyzko–Schönhage algorithm which speeds it up considerably. When used along the critical line, it is often useful to use it in a form where it becomes a formula for the Z function
.
If M and N are non-negative integers, then the zeta function is equal to
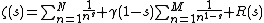
where
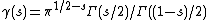
is the factor appearing in the functional equation ζ(s) = γ(s) ζ(1 − s), and

is a contour integral whose contour starts and ends at +∞ and circles the singularities of absolute value at most 2πM. The approximate functional equation gives an estimate for the size of the error term.
and derive the Riemann–Siegel formula from this by applying the method of steepest descent to this integral to give an asymptotic expansion for the error term R(s) as a series of negative powers of Im(s).
In applications s is usually on the critical line, and the positive integers M and N are chosen to be about (2π Im(s))1/2. found good bounds for the error of the Riemann–Siegel formula.
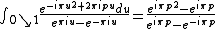
where the contour of integration is a line of slope −1 passing between 0 and 1 .
He used this to give the following integral formula for the zeta function:
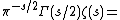
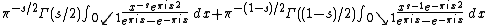
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
dating from the 1850s. Siegel derived it from the Riemann–Siegel integral formula, an expression for the zeta function involving contour integrals. It is often used to compute values of the Riemann–Siegel formula, sometimes in combination with the Odlyzko–Schönhage algorithm which speeds it up considerably. When used along the critical line, it is often useful to use it in a form where it becomes a formula for the Z function
Z function
In mathematics, the Z-function is a function used for studying theRiemann zeta-function along the critical line where the real part of theargument is one-half.It is also called the Riemann-Siegel Z-function,the Riemann-Siegel zeta-function,...
.
If M and N are non-negative integers, then the zeta function is equal to
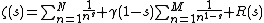
where
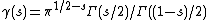
is the factor appearing in the functional equation ζ(s) = γ(s) ζ(1 − s), and

is a contour integral whose contour starts and ends at +∞ and circles the singularities of absolute value at most 2πM. The approximate functional equation gives an estimate for the size of the error term.
and derive the Riemann–Siegel formula from this by applying the method of steepest descent to this integral to give an asymptotic expansion for the error term R(s) as a series of negative powers of Im(s).
In applications s is usually on the critical line, and the positive integers M and N are chosen to be about (2π Im(s))1/2. found good bounds for the error of the Riemann–Siegel formula.
Riemann's integral formula
Riemann showed that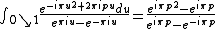
where the contour of integration is a line of slope −1 passing between 0 and 1 .
He used this to give the following integral formula for the zeta function: