
Ray transfer matrix analysis
Encyclopedia
Ray transfer matrix analysis (also known as ABCD matrix analysis) is a type of ray tracing
technique used in the design of some optical
systems, particularly laser
s. It involves the construction of a ray transfer matrix which describes the optical system; tracing of a light path through the system can then be performed by multiplying this matrix with a vector
representing the light ray.
The technique, described below, uses the paraxial approximation
of ray optics, i.e., all rays are assumed to be at a small angle (θ) and a small distance (x) relative to the optical axis
of the system. The approximation is valid as long as sin(θ)≈θ (where θ is measured in radian
s). [An exact method for tracing meridional rays is available, inter alia, at.
These quantities are related by the expression
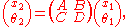
where
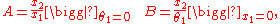
and
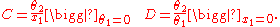
This relates the ray vectors at the input and output planes by the ray transfer matrix (RTM) M, which represents the optical system between the two reference planes. A thermodynamics
argument based on the blackbody radiation can be used to show that the determinant
of a RTM is the ratio of the indices of refraction:
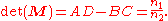
As a result, if the input and output planes are located within the same medium, or within two different media which happen to have identical indices of refraction, then the determinant of M is simply equal to 1.
A similar technique can be used to analyze electrical circuits. See Two-port network
s.
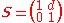 ,
,
where d is the separation distance (measured along the optical axis) between the two reference planes. The ray transfer equation thus becomes:
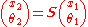 ,
,
and this relates the parameters of the two rays as:
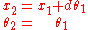
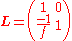 ,
,
where f is the focal length
of the lens. To describe combinations of optical components, ray transfer matrices may be multiplied together to obtain an overall RTM for the compound optical system. For the example of free space of length d followed by a lens of focal length f:
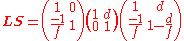 .
.
Note that, since the multiplication of matrices is non-commutative, this is not the same RTM as that for a lens followed by free space:
 .
.
Thus the matrices must be ordered appropriately. Other matrices can be constructed to represent interfaces with media of different refractive indices
, reflection from mirror
s, etc.
and radius of curvature
R, separated by some distance d. For the purposes of ray tracing, this is equivalent to a series of identical thin lenses of focal length f=R/2, each separated from the next by length d. This construction is known as a lens equivalent duct or lens equivalent waveguide
. The RTM of each section of the waveguide is, as above,
 .
.
RTM analysis can now be used to determine the stability of the waveguide (and equivalently, the resonator). That is, it can be determined under what conditions light travelling down the waveguide will be periodically refocussed and stay within the waveguide. To do so, we can find all ray vectors where the output of each section of the waveguide is equal to the input vector multiplied by some real or complex constant λ:
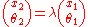 .
.
This gives:
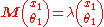 ,
,
which is an eigenvalue equation:
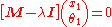
where I is the 2x2 identity matrix
.
Simplifying, we have
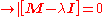
which leads to the characteristic equation

where

is the trace
of the RTM, and
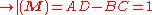
is the determinant
of the RTM. Simplifying, we have
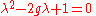
where
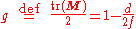
is the stability parameter. The eigenvalues are the solutions of the characteristic equation. From the quadratic formula, we find

After N passes through the system, we have:
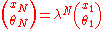 .
.
If the waveguide is stable, λN must not grow without limit. This observation implies that λ cannot take on purely real
values, but must have a non-zero imaginary part. Thus,
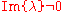
As a result,
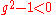
or

Solving the eigenvalue equation gives us a periodic solution of the form:
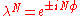 ,
,
or
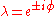 ,
,
where

The technique may be generalised for more complex resonators by constructing a suitable matrix M for the cavity from the matrices of the components present.
s. If we have a Gaussian beam of wavelength λ, radius of curvature R and beam spot size w, it is possible to define a complex beam parameter
q by:
 .
.
This beam can be propagated through an optical system with a given ray transfer matrix by using the equation:
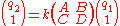 ,
,
where k is a normalisation constant chosen to keep the second component of the ray vector equal to 1. Using matrix multiplication
, this equation expands as
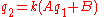
and
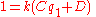
Dividing the first equation by the second eliminates the normalisation constant:
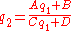 ,
,
It is often convenient to express this last equation in reciprocal form:
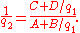
Ray tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces,...
technique used in the design of some optical
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
systems, particularly laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
s. It involves the construction of a ray transfer matrix which describes the optical system; tracing of a light path through the system can then be performed by multiplying this matrix with a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
representing the light ray.
The technique, described below, uses the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
of ray optics, i.e., all rays are assumed to be at a small angle (θ) and a small distance (x) relative to the optical axis
Optical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
of the system. The approximation is valid as long as sin(θ)≈θ (where θ is measured in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s). [An exact method for tracing meridional rays is available, inter alia, at
Definition of the ray transfer matrix
The ray tracing technique is based on two reference planes, called the input and output planes, each perpendicular to the optical axis of the system. Without loss of generality, we will define the optical axis so that it coincides with the z-axis of a fixed coordinate system. A light ray enters the system when the ray crosses the input plane at a distance x1 from the optical axis while traveling in a direction that makes an angle θ1 with the optical axis. Some distance further along, the ray crosses the output plane, this time at a distance x2 from the optical axis and making an angle θ2. n1 and n2 are the indices of refraction of the medium in the input and output plane, respectively.These quantities are related by the expression
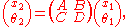
where
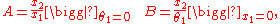
and
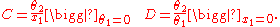
This relates the ray vectors at the input and output planes by the ray transfer matrix (RTM) M, which represents the optical system between the two reference planes. A thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
argument based on the blackbody radiation can be used to show that the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a RTM is the ratio of the indices of refraction:
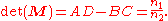
As a result, if the input and output planes are located within the same medium, or within two different media which happen to have identical indices of refraction, then the determinant of M is simply equal to 1.
A similar technique can be used to analyze electrical circuits. See Two-port network
Two-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
s.
Some examples
- For example, if there is free space between the two planes, the ray transfer matrix is given by:
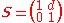 ,
,where d is the separation distance (measured along the optical axis) between the two reference planes. The ray transfer equation thus becomes:
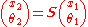 ,
,and this relates the parameters of the two rays as:
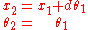
- Another simple example is that of a thin lensThin lens[Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d...
. Its RTM is given by:
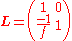 ,
,where f is the focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
of the lens. To describe combinations of optical components, ray transfer matrices may be multiplied together to obtain an overall RTM for the compound optical system. For the example of free space of length d followed by a lens of focal length f:
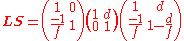 .
.Note that, since the multiplication of matrices is non-commutative, this is not the same RTM as that for a lens followed by free space:
 .
.Thus the matrices must be ordered appropriately. Other matrices can be constructed to represent interfaces with media of different refractive indices
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
, reflection from mirror
Mirror
A mirror is an object that reflects light or sound in a way that preserves much of its original quality prior to its contact with the mirror. Some mirrors also filter out some wavelengths, while preserving other wavelengths in the reflection...
s, etc.
Table of ray transfer matrices
for simple optical components| Element | Matrix | Remarks |
|---|---|---|
| Propagation in free space or in a medium of constant refractive index | 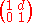 |
d = distance |
| Refraction at a flat interface | 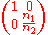 |
n1 = initial refractive index n2 = final refractive index. |
| Refraction at a curved interface | 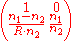 |
R = radius of curvature, R > 0 for convex (centre of curvature after interface) n1 = initial refractive index n2 = final refractive index. |
| Reflection from a flat mirror | 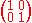 |
|
| Reflection from a curved mirror | 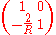 |
R = radius of curvature, R > 0 for concave |
| Thin lens |  |
f = focal length of lens where f > 0 for convex/positive (converging) lens. Only valid if the focal length is much greater than the thickness of the lens. |
| Single right angle prism | 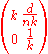 |
k = (cos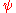 /cos /cos ) is the beam expansion ) is the beam expansionBeam expander Beam expanders are used in laser physics either as intracavity or extracavity elements. They can be telescopic in nature or prismatic. Generally prismatic beam expanders use several prisms and are known as multiple-prism beam expanders.... factor, where  is the angle of incidence, is the angle of incidence,  is the angle of refraction, d = prism path length, n = refractive index of the prism material. This matrix applies for orthogonal beam exit. is the angle of refraction, d = prism path length, n = refractive index of the prism material. This matrix applies for orthogonal beam exit. |
Resonator stability
RTM analysis is particularly useful when modeling the behaviour of light in optical resonators, such as those used in lasers. At its simplest, an optical resonator consists of two identical facing mirrors of 100% reflectivityReflectivity
In optics and photometry, reflectivity is the fraction of incident radiation reflected by a surface. In general it must be treated as a directional property that is a function of the reflected direction, the incident direction, and the incident wavelength...
and radius of curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
R, separated by some distance d. For the purposes of ray tracing, this is equivalent to a series of identical thin lenses of focal length f=R/2, each separated from the next by length d. This construction is known as a lens equivalent duct or lens equivalent waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
. The RTM of each section of the waveguide is, as above,
 .
.RTM analysis can now be used to determine the stability of the waveguide (and equivalently, the resonator). That is, it can be determined under what conditions light travelling down the waveguide will be periodically refocussed and stay within the waveguide. To do so, we can find all ray vectors where the output of each section of the waveguide is equal to the input vector multiplied by some real or complex constant λ:
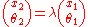 .
.This gives:
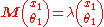 ,
,which is an eigenvalue equation:
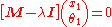
where I is the 2x2 identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
Simplifying, we have
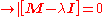
which leads to the characteristic equation
Characteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...

where

is the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the RTM, and
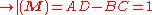
is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the RTM. Simplifying, we have
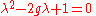
where
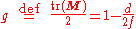
is the stability parameter. The eigenvalues are the solutions of the characteristic equation. From the quadratic formula, we find

After N passes through the system, we have:
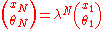 .
.If the waveguide is stable, λN must not grow without limit. This observation implies that λ cannot take on purely real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
values, but must have a non-zero imaginary part. Thus,
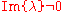
As a result,
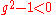
or

Solving the eigenvalue equation gives us a periodic solution of the form:
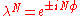 ,
,or
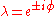 ,
,where

The technique may be generalised for more complex resonators by constructing a suitable matrix M for the cavity from the matrices of the components present.
Ray transfer matrices for Gaussian beams
The matrix formalism is also useful to describe Gaussian beamGaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity distributions are well approximated by Gaussian functions. Many lasers emit beams that approximate a Gaussian profile, in which case the laser is said to be operating on the fundamental...
s. If we have a Gaussian beam of wavelength λ, radius of curvature R and beam spot size w, it is possible to define a complex beam parameter
Complex beam parameter
In optics, the complex beam parameter is a complex number that specifies the properties of a Gaussian beam at a particular point z along the axis of the beam. It is usually denoted by q...
q by:
 .
.This beam can be propagated through an optical system with a given ray transfer matrix by using the equation:
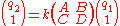 ,
,where k is a normalisation constant chosen to keep the second component of the ray vector equal to 1. Using matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, this equation expands as
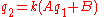
and
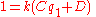
Dividing the first equation by the second eliminates the normalisation constant:
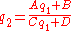 ,
,It is often convenient to express this last equation in reciprocal form:
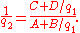
See also
- Transfer-matrix method (optics)Transfer-matrix method (optics)The transfer-matrix method is a method used in optics and acoustics to analyze the propagation of electromagnetic or acoustic waves through a stratified medium. This is for example relevant for the design of anti-reflective coatings and dielectric mirrors.The reflection of light from a single...
- Two-port networkTwo-port networkA two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
- Linear canonical transformationLinear canonical transformationIn Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
External links
- Thick lenses (Matrix methods)
- ABCD Matrices Tutorial Provides an example for a system matrix of an entire system.
- ABCD Calculator An interactive calculator to help solve ABCD matrices.

