Quarter-comma meantone
Encyclopedia
Quarter-comma meantone, or 1/4-comma meantone, was the most common meantone temperament
in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning
. The difference is that in this system the perfect fifth
is flattened by one quarter of a syntonic comma
, with respect to its just intonation
used in Pythagorean tuning (frequency ratio
3:2). The purpose is to obtain justly intonated major third
s (with a frequency ratio equal to 5:4). It was described by Pietro Aron
(also spelled Aaron), in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino
and Francisco de Salinas
described the tuning with mathematical exactitude.
s, with the diatonic semitone larger. In Pythagorean tuning, these correspond to the Pythagorean limma and the Pythagorean apotome, only now the apotome is larger. In any meantone or Pythagorean tuning, a whole tone is composed of two semitones of each kind, a major third
is two whole tones and therefore consists of two semitones of each kind, a perfect fifth
of meantone contains four diatonic and three chomatic semitones, and an octave
seven diatonic and five chromatic semitones, it follows that:
Thus, in Pythagorean tuning, where sequences of just
fifths (frequency ratio
3:2) and octaves are used to produce the other intervals, a whole tone is
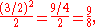
and a major third is
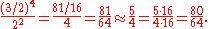
An interval of a seventeenth, consisting of sixteen diatonic and twelve chromatic semitones, such as the interval from D4 to F6, can be equivalently obtained using either
This large interval of a seventeenth contains (5 + (5 − 1) + (5 − 1) + (5 − 1) = 20 − 3 = 17 staff positions). In Pythagorean tuning, the size of a seventeenth is defined using a stack of four justly tuned fifths (frequency ratio 3:2):
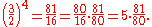
In quarter-comma meantone temperament, where a just
major third (5:4) is required, a slightly narrower seventeenth is obtained by stacking two octaves (4:1) and a major third:
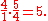
By definition, however, a seventeenth of the same size (5:1) must be obtained, even in quarter-comma meantone, by stacking four fifths. Since justly tuned fifths, such as those used in Pythagorean tuning, produce a slightly wider seventeenth, in quarter-comma meantone the fifths must be slightly flattened to meet this requirement. Letting x be the frequency ratio of the flattened fifth, it is desired that four fifths have a ratio of 5:1,
which implies that a fifth is
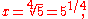
a whole tone, built by moving two fifths up and one octave down, is
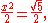
and a diatonic semitone, built by moving three octaves up and five fifths down, is
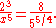
Notice that, in quarter-comma meantone, the seventeenth is 81/80 times narrower than in Pythagorean tuning. This difference in size, equal to about 21.506 cents, is called the syntonic comma
. This implies that the fifth is a quarter of a syntonic comma narrower than the justly tuned Pythagorean fifth. Namely, this system tunes the fifths in the ratio of
which is slightly smaller (or flatter) than the ratio of a justly tuned fifth:
The difference between these two sizes is a quarter of a syntonic comma:
In sum, this system tunes the major thirds to the just
ratio of 5:4 (so, for instance, if A is tuned to 440 Hz
, C' is tuned to 550 Hz), most of the whole tones (namely the major second
s) in the ratio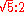
, and most of the semitones (namely the diatonic semitones or minor second
s) in the ratio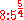
. This is achieved by tuning the seventeenth a syntonic comma flatter than the Pythagorean seventeenth, which implies tuning the fifth a quarter of a syntonic comma flatter than the just
ratio of 3:2. It is this that gives the system its name of quarter-comma meantone.
for a more detailed explanation).
For each note in the basic octave, the table provides the conventional name of the interval
from D (the base note), the formula to compute its frequency ratio, and the approximate values for its frequency ratio and size in cents.
In the formulas,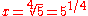
is the size of the tempered perfect fifth, and the ratios x:1 or 1:x represent an ascending or descending tempered perfect fifth (i.e. an increase or decrease in frequency by x), while 2:1 or 1:2 represent an ascending or descending octave.
As in Pythagorean tuning, this method generates 13 pitches, but A and G have almost the same frequency, and to build a 12-tone scale A is typically discarded (although the choice between these two notes is completely arbitrary).
Except for the size of the fifth, this is identical to the stack traditionally used in Pythagorean tuning
. Some authors prefer showing a C-based stack of fifths, ranging from A to G. Since C is not at its center, this stack is called C-based asymmetric:
Since the boundaries of this stack (A and G) are identical to those of the D-based symmetric stack, the 12 tone scale produced by this stack is also identical. The only difference is that the construction table shows intervals from C, rather than from D. Notice that 144 intervals can be formed from a 12 tone scale (see table below), which include intervals from C, D, and any other note. However, the construction table shows only 12 of them, in this case those starting from C. This is at the same time the main advantage and main disadvantage of the C-based asymmetric stack, as the intervals from C are commonly used, but since C is not at the center of this stack, they unfortunately include an augmented fifth
(or A5, i.e. the interval from C to G), instead of a minor sixth
(m6). This A5 is an extremely dissonant wolf interval
, as it deviates by 41.1 cents (a diesis
of ratio 128:125, almost twice a syntonic comma
!) from the corresponding pure interval of 8/5 or 813.7 cents.
On the contrary, the intervals from D shown in the table above, since D is at the center of the stack, do not include wolf intervals and include a pure m6 (from D to B), instead of an impure A5. Notice that in the above mentioned set of 144 intervals pure m6's are more frequently observed than impure A5's (see table below), and this is one of the reasons why it is not desirable to show an impure A5 in the construction table. A C-based symmetric stack might be also used, to avoid the above mentioned drawback:
In this stack, G and F have a similar frequency, and G is typically discarded. Also, the note between C and D is called D rather than C, and the note between G and A is called A rather than G. The C-based symmetric stack is rarely used, possibly because it produces the wolf fifth in the unusual position of F—D instead of G—E, where musicians using Pythagorean tuning were used to find it).
version of the quarter-comma meantone temperament may be constructed in the same way as Johann Kirnberger
's rational version
of 12-TET. The value of 51/8 351/3 is very close to 4, that's why a 7-limit interval 6144:6125 (which is the difference between the 5-limit diesis
128:125 and the septimal diesis
49:48), equal to 5.362 cents, appears very close to the quarter-comma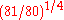
of 5.377 cents. So the perfect fifth has the ratio of 6125:4096, which is the difference between three just major thirds and two septimal major seconds; four such fifths exceed the ratio of 5:1 by the tiny interval of 0.058 cents. The wolf fifth
there appears to be 49:32, the difference between the septimal minor seventh and the septimal major second.
The tones in the diatonic scale can be divided into pairs of semitones. However, since S2 is not equal to T, each tone must be composed of a pair of unequal semitones, S, and X:
Hence,
Notice that S is 117.1 cents, and X is 76.0 cents. Thus, S is the greater semitone, and X is the lesser one. S is commonly called the diatonic semitone (or minor second
), while X is called the chromatic semitone (or augmented unison
).
The sizes of S and X can be compared to the just intonated ratio 18/17 which is 99.0 cents. S deviates from it by +18.2 cents, and X by −22.9 cents. These two deviations are comparable to the syntonic comma (21.5 cents), which this system is designed to tune out from the Pythagorean major third. However, since even the just intonated ratio 18/17 sounds markedly dissonant, these deviations are considered acceptable in a semitone.
s, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
As explained above, one of the twelve fifths (the wolf fifth) has a different size with respect to the other eleven. For a similar reason, each of the other interval types, except for the unisons and the octaves, has two different sizes in quarter-comma meantone. This is the price paid for seeking just intonation
. The table below shows their approximate size in cents. Interval names are given in their standard shortened form. For instance, the size of the interval from D to A, which is a perfect fifth (P5), can be found in the seventh column of the row labeled D. Strictly just (or pure) intervals are shown in bold font. Wolf interval
s are highlighted in red.
Surprisingly, although this tuning system was designed to produce pure major thirds, only 8 of them are pure (5:4 or about 386.3 cents).
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, as mentioned above, the frequencies defined by construction for the twelve notes determine two different kinds of semitones (i.e. intervals between adjacent notes):
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly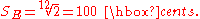
As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
For a comparison with other tuning systems, see also this table.
By definition, in quarter-comma meantone 11 perfect fifths (P5 in the table) have a size of approximately 696.6 cents (700−ε cents, where ε ≈ 3.422 cents); since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of 700+11ε cents, which is about 737.6 cents (the wolf fifth). Notice that, as shown in the table, the latter interval, although enharmonically equivalent to a fifth, is more properly called a diminished sixth
(d6). Similarly,
In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε, the difference between the 1/4-comma meantone fifth and the average fifth.
Notice that, as an obvious consequence, each augmented or diminished interval is exactly 12ε cents (≈ 41.1 cents) wider or narrower than its enharmonic equivalent. For instance, the d6 (or wolf fifth) is 12ε cents wider than each P5, and each A2 is 12ε cents narrower than each m3. This interval of size 12ε is known as a diesis
, or diminished second
. This implies that ε can be also defined as one twelfth of a diesis.
(interval spanning 4 semitones) and a perfect fifth
(7 semitones). The minor triad can likewise be defined by a minor third
(3 semitones) and a perfect fifth (7 semitones).
As shown above, a chromatic scale has twelve intervals spanning seven semitones. Eleven of these are perfect fifths (P5), while the twelfth is a diminished sixth (d6). Since they span the same number of semitones, P5 and d6 are considered to be enharmonically equivalent. In an equally
tuned chromatic scale, P5 and d6 have exactly the same size. The same is true for all the enharmonically equivalent intervals spanning 4 semitones (M3 and d4), or 3 semitones (m3 and A2). However, in the meantone temperament this is not true. In this tuning system, enharmonically equivalent intervals may have different sizes, and some intervals may markedly deviate from their justly tuned
ideal ratios. As explained in the previous section, if the deviation is too large, then the given interval is not usable, either by itself or in a chord.
The following table focuses only on the above-mentioned three interval types, used to form major and minor triads. Each row shows three intervals of different types but which have the same root note. Each interval is specified by a pair of notes. To the right of each interval is listed the formula for the interval ratio
. The intervals d4, d6 and A2 may be regarded as wolf interval
s, and have been marked in red
. S and X denote the ratio of the two above-mentioned kinds of semitones (m2 and A1).
First, look at the last two columns on the right. All the 7-semitone intervals except one have a ratio of
which deviates by −5.4 cents from the just 3:2 of 702.0 cents. Five cents is small and acceptable. On the other hand, the d6 from G to E has a ratio of
which deviates by +35.7 cents from the just fifth. Thirty-five cents is beyond the acceptable range.
Now look at the two columns in the middle. Eight of the twelve 4-semitone intervals have a ratio of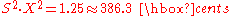
which is exactly a just 5:4. On the other hand, the four d4 with roots at C, F, G and B have a ratio of
which deviates by +41.1 cents from the just M3. Again, this sounds badly out of tune.
Major triads are formed out of both major thirds and perfect fifths. If either of the two intervals is substituted by a wolf interval (d6 instead of P5, or d4 instead of M3), then the triad is not acceptable. Therefore major triads with root notes of C, F, G and B are not used in meantone scales whose fundamental note is C.
Now look at the first two columns on the left. Nine of the twelve 3-semitone intervals have a ratio of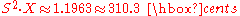
which deviates by −5.4 cents from the just 6:5 of 315.6 cents. Five cents is acceptable. On the other hand, the three augmented seconds whose roots are E, F and B have a ratio of
which deviates by −46.4 cents from the just minor third. It is a close match, however, for the 7:6 septimal minor third
of 266.9 cents, deviating by +2.3 cents. These augmented seconds, though sufficiently consonant by themselves, will sound "exotic" or atypical when plaied together with a perfect fifth.
Minor triads are formed out of both minor thirds and fifths. If either of the two intervals are substituted by an enharmonically equivalent interval (d6 instead of P5, or A2 instead of m3), then the triad will not sound good. Therefore minor triads with root notes of E, F, G and B are not used in the meantone scale defined above.
The following major triads are usable: C, D, E, E, F, G, A, B.
The following minor triads are usable: C, C, D, E, F, G, A, B.
The following root notes are useful for both major and minor triads: C, D, E, G and A. Notice that these five pitches form a major pentatonic scale
.
The following root notes are useful only for major triads: E, F, B.
The following root notes are useful only for minor triads: C, F, B.
The following root note is useful for neither major nor minor triad: G.
It can be verified through calculation that most whole tones (namely, the major seconds) are composed of one greater and one lesser semitone:
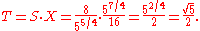
Similarly, a fifth is typically composed of three tones and one greater semitone:
which is equivalent to four greater and three lesser semitones:
can be constructed by starting from the fundamental note and multiplying it either by T to move up by a tone or by S to move up by a semitone.
C D E F G A B C'
|----|----|----|----|----|----|----|
T T S T T T S
The resulting interval sizes with respect to the base note C are shown in the following table:
can proceed by stacking a series of 12 semitones, each of which may be either diatonic (S) or chromatic (X).
C C D E E F F G G A B B C'
|----|----|----|----|----|----|----|----|----|----|----|----|
X S S X S X S X S S X S
Notice that this scale is an extension of the diatonic scale shown in the previous table. Only five notes have been added: C, E, F, G and B (a pentatonic scale
).
As explained above, an identical scale was originally defined and produced by using a sequence of tempered fifths, ranging from E (five fifths below D) to G (six fifths above D), rather than a sequence of semitones. This more conventional approach, similar to the D-based Pythagorean tuning
system, explains the reason why the X and S semitones are arranged in the particular and apparently arbitrary sequence shown above.
The interval sizes with respect to the base note C are presented in the following table. The frequency ratios are computed as shown by the formulas. Delta is the difference in cents between meantone and 12-TET. 1/4-c is the difference in quarter-commas between meantone and Pythagorean tuning.
and in fact transcendental
; hence a chain of meantone fifths, like a chain of pure 3/2 fifths, never closes (i.e. never equals a chain of octaves). However, the continued fraction
approximations to this irrational fraction number allow us to find equal divisions of the octave which do close; the denominators of these are 1, 2, 5, 7, 12, 19, 31, 174, 205, 789 ... From this we find that 31 quarter-comma meantone fifths come close to closing, and conversely 31 equal temperament
represents a good approximation to quarter-comma meantone. See: schisma
.
Meantone temperament
Meantone temperament is a musical temperament, which is a system of musical tuning. In general, a meantone is constructed the same way as Pythagorean tuning, as a stack of perfect fifths, but in meantone, each fifth is narrow compared to the ratio 27/12:1 in 12 equal temperament, the opposite of...
in the sixteenth and seventeenth centuries, and was sometimes used later. This method is a variant of Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
. The difference is that in this system the perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
is flattened by one quarter of a syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
, with respect to its just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
used in Pythagorean tuning (frequency ratio
Interval ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498...
3:2). The purpose is to obtain justly intonated major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
s (with a frequency ratio equal to 5:4). It was described by Pietro Aron
Pietro Aron
Pietro Aron, also known as Pietro Aaron , was an Italian music theorist and composer. He was born in Florence and probably died in Bergamo .-Biography:...
(also spelled Aaron), in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino
Gioseffo Zarlino
Gioseffo Zarlino was an Italian music theorist and composer of the Renaissance. He was possibly the most famous music theorist between Aristoxenus and Rameau, and made a large contribution to the theory of counterpoint as well as to musical tuning.-Life:Zarlino was born in Chioggia, near Venice...
and Francisco de Salinas
Francisco de Salinas
Francisco de Salinas was a Spanish music theorist and organist, noted as among the first to describe meantone temperament in mathematically precise terms, and one of the first to describe, in effect, 19 equal temperament. In his De musica libri septem of 1577 he discusses 1/3-, 1/4- and 2/7-comma...
described the tuning with mathematical exactitude.
Construction
In a meantone tuning, we have diatonic and chromatic semitoneSemitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s, with the diatonic semitone larger. In Pythagorean tuning, these correspond to the Pythagorean limma and the Pythagorean apotome, only now the apotome is larger. In any meantone or Pythagorean tuning, a whole tone is composed of two semitones of each kind, a major third
Major third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
is two whole tones and therefore consists of two semitones of each kind, a perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
of meantone contains four diatonic and three chomatic semitones, and an octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
seven diatonic and five chromatic semitones, it follows that:
- Five fifths down and three octaves up make up a diatonic semitone, so that the Pythagorean limma is tempered to a diatonic semitone.
- Two fifths up and an octave down make up a whole tone consisting of one diatonic and one chromatic semitone.
- Four fifths up and two octaves down make up a major third, consisting of two diatonic and two chromatic semitones, or in other words two whole tones.
Thus, in Pythagorean tuning, where sequences of just
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
fifths (frequency ratio
Interval ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498...
3:2) and octaves are used to produce the other intervals, a whole tone is
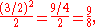
and a major third is
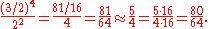
An interval of a seventeenth, consisting of sixteen diatonic and twelve chromatic semitones, such as the interval from D4 to F6, can be equivalently obtained using either
- a stack of four fifths (e.g. D4—A4—E5—B5—F6), or
- a stack of two octaves and one major third (e.g. D4—D5—D6—F6).
This large interval of a seventeenth contains (5 + (5 − 1) + (5 − 1) + (5 − 1) = 20 − 3 = 17 staff positions). In Pythagorean tuning, the size of a seventeenth is defined using a stack of four justly tuned fifths (frequency ratio 3:2):
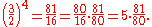
In quarter-comma meantone temperament, where a just
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
major third (5:4) is required, a slightly narrower seventeenth is obtained by stacking two octaves (4:1) and a major third:
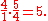
By definition, however, a seventeenth of the same size (5:1) must be obtained, even in quarter-comma meantone, by stacking four fifths. Since justly tuned fifths, such as those used in Pythagorean tuning, produce a slightly wider seventeenth, in quarter-comma meantone the fifths must be slightly flattened to meet this requirement. Letting x be the frequency ratio of the flattened fifth, it is desired that four fifths have a ratio of 5:1,
which implies that a fifth is
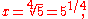
a whole tone, built by moving two fifths up and one octave down, is
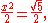
and a diatonic semitone, built by moving three octaves up and five fifths down, is
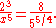
Notice that, in quarter-comma meantone, the seventeenth is 81/80 times narrower than in Pythagorean tuning. This difference in size, equal to about 21.506 cents, is called the syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
. This implies that the fifth is a quarter of a syntonic comma narrower than the justly tuned Pythagorean fifth. Namely, this system tunes the fifths in the ratio of
which is slightly smaller (or flatter) than the ratio of a justly tuned fifth:
The difference between these two sizes is a quarter of a syntonic comma:
In sum, this system tunes the major thirds to the just
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
ratio of 5:4 (so, for instance, if A is tuned to 440 Hz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
, C' is tuned to 550 Hz), most of the whole tones (namely the major second
Major second
In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
s) in the ratio
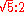, and most of the semitones (namely the diatonic semitones or minor secondMinor second
In modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D....
s) in the ratio
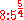. This is achieved by tuning the seventeenth a syntonic comma flatter than the Pythagorean seventeenth, which implies tuning the fifth a quarter of a syntonic comma flatter than the justJust intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
ratio of 3:2. It is this that gives the system its name of quarter-comma meantone.
12-tone scale
The whole chromatic scale (a subset of which is the diatonic scale), can be constructed by starting from a given base note, and increasing or decreasing its frequency by one or more fifths. This method is identical to Pythagorean tuning, except for the size of the fifth, which is tempered as explained above. The construction table below illustrates how the pitches of the notes are obtained with respect to D (the base note), in a D-based scale (see Pythagorean tuningPythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
for a more detailed explanation).
For each note in the basic octave, the table provides the conventional name of the interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
from D (the base note), the formula to compute its frequency ratio, and the approximate values for its frequency ratio and size in cents.
| Note | Interval from D | Formula | Freq. ratio |
Size (cents) |
|---|---|---|---|---|
| A | diminished fifth |  |
1.4311 | 620.5 |
| E | minor second Minor second In modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D.... |
 |
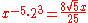1.0700 | 117.1 |
| B | minor sixth Minor sixth -Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7.... |
 |
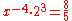1.6000 | 813.7 |
| F | minor third Minor third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major... |
 |
1.1963 | 310.3 |
| C | minor seventh Minor seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the minor seventh is one of two commonly occurring sevenths. The minor quality specification identifies it as being the smallest of the two: the minor seventh spans ten semitones, the... |
 |
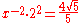1.7889 | 1006.8 |
| G | perfect fourth Perfect fourth In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there... |
 |
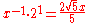1.3375 | 503.4 |
| D | unison Unison In music, the word unison can be applied in more than one way. In general terms, it may refer to two notes sounding the same pitch, often but not always at the same time; or to the same musical voice being sounded by several voices or instruments together, either at the same pitch or at a distance... |
 |
1.0000 | 0.0 |
| A | perfect fifth Perfect fifth In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones... |
 |
1.4953 | 696.6 |
| E | major second Major second In Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions... |
 |
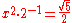1.1180 | 193.2 |
| B | major sixth Major sixth In classical music from Western culture, a sixth is a musical interval encompassing six staff positions , and the major sixth is one of two commonly occurring sixths. It is qualified as major because it is the largest of the two... |
 |
1.6719 | 889.7 |
| F | major third Major third In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three... |
 |
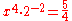1.2500 | 386.3 |
| C | major seventh Major seventh In classical music from Western culture, a seventh is a musical interval encompassing seven staff positions , and the major seventh is one of two commonly occurring sevenths. It is qualified as major because it is the larger of the two... |
 |
1.8692 | 1082.9 |
| G | augmented fourth |  |
1.3975 | 579.5 |
In the formulas,
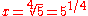is the size of the tempered perfect fifth, and the ratios x:1 or 1:x represent an ascending or descending tempered perfect fifth (i.e. an increase or decrease in frequency by x), while 2:1 or 1:2 represent an ascending or descending octave.As in Pythagorean tuning, this method generates 13 pitches, but A and G have almost the same frequency, and to build a 12-tone scale A is typically discarded (although the choice between these two notes is completely arbitrary).
C- based construction tables
The table above shows a D-based stack of fifths (i.e. a stack in which all ratios are expressed relative to D, and D has a ratio of 1/1). Since it is centered at D, the base note, this stack can be called D-based symmetric:- A—E—B—F—C—G—D—A—E—B—F—C—G
Except for the size of the fifth, this is identical to the stack traditionally used in Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
. Some authors prefer showing a C-based stack of fifths, ranging from A to G. Since C is not at its center, this stack is called C-based asymmetric:
- A—E—B—F—C—G—D—A—E—B—F—C—G
Since the boundaries of this stack (A and G) are identical to those of the D-based symmetric stack, the 12 tone scale produced by this stack is also identical. The only difference is that the construction table shows intervals from C, rather than from D. Notice that 144 intervals can be formed from a 12 tone scale (see table below), which include intervals from C, D, and any other note. However, the construction table shows only 12 of them, in this case those starting from C. This is at the same time the main advantage and main disadvantage of the C-based asymmetric stack, as the intervals from C are commonly used, but since C is not at the center of this stack, they unfortunately include an augmented fifth
Augmented fifth
In classical music from Western culture, an augmented fifth is an interval produced by widening a perfect fifth by a chromatic semitone. For instance, the interval from C to G is a perfect fifth, seven semitones wide, and both the intervals from C to G, and from C to G are augmented fifths,...
(or A5, i.e. the interval from C to G), instead of a minor sixth
Minor sixth
-Subminor sixth:In music, a subminor sixth or septimal sixth is an interval that is noticeably narrower than a minor sixth but noticeably wider than a diminished sixth.The sub-minor sixth is an interval of a 14:9 ratio or alternately 11:7....
(m6). This A5 is an extremely dissonant wolf interval
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
, as it deviates by 41.1 cents (a diesis
Diesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
of ratio 128:125, almost twice a syntonic comma
Syntonic comma
In music theory, the syntonic comma, also known as the chromatic diesis, the comma of Didymus, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80, or around 21.51 cents...
!) from the corresponding pure interval of 8/5 or 813.7 cents.
On the contrary, the intervals from D shown in the table above, since D is at the center of the stack, do not include wolf intervals and include a pure m6 (from D to B), instead of an impure A5. Notice that in the above mentioned set of 144 intervals pure m6's are more frequently observed than impure A5's (see table below), and this is one of the reasons why it is not desirable to show an impure A5 in the construction table. A C-based symmetric stack might be also used, to avoid the above mentioned drawback:
- G—D—A—E—B—F—C—G—D—A—E—B—F
In this stack, G and F have a similar frequency, and G is typically discarded. Also, the note between C and D is called D rather than C, and the note between G and A is called A rather than G. The C-based symmetric stack is rarely used, possibly because it produces the wolf fifth in the unusual position of F—D instead of G—E, where musicians using Pythagorean tuning were used to find it).
Justly intonated quarter-comma meantone
A just intonationJust intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
version of the quarter-comma meantone temperament may be constructed in the same way as Johann Kirnberger
Johann Kirnberger
Johann Philipp Kirnberger was a musician, composer , and music theorist. A pupil of Johann Sebastian Bach, he became a violinist at the court of Frederick II of Prussia in 1751. He was the music director to the Prussian Princess Anna Amalia from 1758 until his death. Kirnberger greatly admired J.S...
's rational version
Schisma
In music, the schisma is the ratio between a Pythagorean comma and a syntonic comma and equals 32805:32768, which is 1.9537 cents...
of 12-TET. The value of 51/8 351/3 is very close to 4, that's why a 7-limit interval 6144:6125 (which is the difference between the 5-limit diesis
Diesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
128:125 and the septimal diesis
Septimal diesis
In music, septimal diesis is an interval with the ratio of 49:48 , which is the difference between the septimal whole tone and the septimal minor third. It is about 35.7 cents wide, which is narrower than a quarter-tone but wider than the septimal comma...
49:48), equal to 5.362 cents, appears very close to the quarter-comma
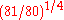of 5.377 cents. So the perfect fifth has the ratio of 6125:4096, which is the difference between three just major thirds and two septimal major seconds; four such fifths exceed the ratio of 5:1 by the tiny interval of 0.058 cents. The wolf fifthWolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
there appears to be 49:32, the difference between the septimal minor seventh and the septimal major second.
Greater and lesser semitones
As discussed above, in the quarter-comma meantone temperament,- the ratio of a semitone is
- the ratio of a tone is
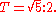
The tones in the diatonic scale can be divided into pairs of semitones. However, since S2 is not equal to T, each tone must be composed of a pair of unequal semitones, S, and X:
Hence,
Notice that S is 117.1 cents, and X is 76.0 cents. Thus, S is the greater semitone, and X is the lesser one. S is commonly called the diatonic semitone (or minor second
Minor second
In modern Western tonal music theory a minor second is the interval between two notes on adjacent staff positions, or having adjacent note letters, whose alterations cause them to be one semitone or half-step apart, such as B and C or C and D....
), while X is called the chromatic semitone (or augmented unison
Augmented unison
In modern Western tonal music theory an augmented unison is the interval between two notes on the same staff position, or having the same note letter, whose alterations cause them, in ordinary equal temperament, to be one semitone apart. In other words, it is a unison where one note has been raised...
).
The sizes of S and X can be compared to the just intonated ratio 18/17 which is 99.0 cents. S deviates from it by +18.2 cents, and X by −22.9 cents. These two deviations are comparable to the syntonic comma (21.5 cents), which this system is designed to tune out from the Pythagorean major third. However, since even the just intonated ratio 18/17 sounds markedly dissonant, these deviations are considered acceptable in a semitone.
Size of intervals
The table above shows only intervals from D. However, intervals can be formed by starting from each of the above listed 12 notes. Thus, twelve intervals can be defined for each interval type (twelve unisons, twelve semitoneSemitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s, twelve intervals composed of 2 semitones, twelve intervals composed of 3 semitones, etc.).
As explained above, one of the twelve fifths (the wolf fifth) has a different size with respect to the other eleven. For a similar reason, each of the other interval types, except for the unisons and the octaves, has two different sizes in quarter-comma meantone. This is the price paid for seeking just intonation
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
. The table below shows their approximate size in cents. Interval names are given in their standard shortened form. For instance, the size of the interval from D to A, which is a perfect fifth (P5), can be found in the seventh column of the row labeled D. Strictly just (or pure) intervals are shown in bold font. Wolf interval
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
s are highlighted in red.
Surprisingly, although this tuning system was designed to produce pure major thirds, only 8 of them are pure (5:4 or about 386.3 cents).
The reason why the interval sizes vary throughout the scale is that the pitches forming the scale are unevenly spaced. Namely, as mentioned above, the frequencies defined by construction for the twelve notes determine two different kinds of semitones (i.e. intervals between adjacent notes):
- The minor second (m2), also called diatonic semitone, with size
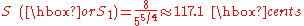
(for instance, between D and E) - The augmented unison (A1), also called chromatic semitone, with size
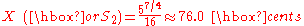
(for instance, between C and C)
Conversely, in an equally tempered chromatic scale, by definition the twelve pitches are equally spaced, all semitones having a size of exactly
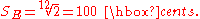
As a consequence all intervals of any given type have the same size (e.g., all major thirds have the same size, all fifths have the same size, etc.). The price paid, in this case, is that none of them is justly tuned and perfectly consonant, except, of course, for the unison and the octave.
For a comparison with other tuning systems, see also this table.
By definition, in quarter-comma meantone 11 perfect fifths (P5 in the table) have a size of approximately 696.6 cents (700−ε cents, where ε ≈ 3.422 cents); since the average size of the 12 fifths must equal exactly 700 cents (as in equal temperament), the other one must have a size of 700+11ε cents, which is about 737.6 cents (the wolf fifth). Notice that, as shown in the table, the latter interval, although enharmonically equivalent to a fifth, is more properly called a diminished sixth
Diminished sixth
In classical music from Western culture, a diminished sixth is an interval produced by narrowing a minor sixth by a chromatic semitone. For example, the interval from A to F is a minor sixth, eight semitones wide, and both the intervals from A to F, and from A to F are diminished sixths, spanning...
(d6). Similarly,
- 10 major secondMajor secondIn Western music theory, a major second is a musical interval spanning two semitones, and encompassing two adjacent staff positions . For example, the interval from C to D is a major second, as the note D lies two semitones above C, and the two notes are notated on adjacent staff postions...
s (M2) are ≈ 193.2 cents (200−2ε), 2 diminished thirdDiminished thirdIn classical music from Western culture, a diminished third is the musical interval produced by narrowing a minor third by a chromatic semitone. For instance, the interval from A to C is a minor third, three semitones wide, and both the intervals from A to C, and from A to C are diminished thirds,...
s (d3) are ≈ 234.2 cents (200+10ε), and their average is 200 cents; - 9 minor thirdMinor thirdIn classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
s (m3) are ≈ 310.3 cents (300+3ε), 3 augmented secondAugmented secondIn classical music from Western culture, an augmented second is an interval produced by widening a major second by a chromatic semitone. For instance, the interval from C to D is a major second, two semitones wide, and both the intervals from C to D, and from C to D are augmented seconds, spanning...
s (A2) are ≈ 269.2 cents (300−9ε), and their average is 300 cents; - 8 major thirdMajor thirdIn classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
s (M3) are ≈ 386.3 cents (400−4ε), 4 diminished fourthDiminished fourthIn classical music from Western culture, a diminished fourth is an interval produced by narrowing a perfect fourth by a chromatic semitone. For example, the interval from C to F is a perfect fourth, five semitones wide, and both the intervals from C to F, and from C to F are diminished fourths,...
s (d4) are ≈ 427.4 cents (400+8ε), and their average is 400 cents; - 7 diatonic semitoneSemitoneA semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically....
s (m2) are ≈ 117.1 cents (100+5ε), 5 chromatic semitones (A1) are ≈ 76.0 cents (100−7ε), and their average is 100 cents.
In short, similar differences in width are observed for all interval types, except for unisons and octaves, and they are all multiples of ε, the difference between the 1/4-comma meantone fifth and the average fifth.
Notice that, as an obvious consequence, each augmented or diminished interval is exactly 12ε cents (≈ 41.1 cents) wider or narrower than its enharmonic equivalent. For instance, the d6 (or wolf fifth) is 12ε cents wider than each P5, and each A2 is 12ε cents narrower than each m3. This interval of size 12ε is known as a diesis
Diesis
In classical music from Western culture, a diesis is either an accidental , or a comma type of musical interval, usually defined as the difference between an octave and three justly tuned major thirds , equal to 128:125 or about 41.06 cents...
, or diminished second
Diminished second
In modern Western tonal music theory a diminished second is the interval between notes on two adjacent staff positions, or having adjacent note letters, whose alterations cause them, in ordinary equal temperament, to have no pitch difference, such as B and C or B and C...
. This implies that ε can be also defined as one twelfth of a diesis.
Triads in the chromatic scale
The major triad can be defined by a pair of intervals from the root note: a major thirdMajor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the major third is one of two commonly occurring thirds. It is qualified as major because it is the largest of the two: the major third spans four semitones, the minor third three...
(interval spanning 4 semitones) and a perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
(7 semitones). The minor triad can likewise be defined by a minor third
Minor third
In classical music from Western culture, a third is a musical interval encompassing three staff positions , and the minor third is one of two commonly occurring thirds. The minor quality specification identifies it as being the smallest of the two: the minor third spans three semitones, the major...
(3 semitones) and a perfect fifth (7 semitones).
As shown above, a chromatic scale has twelve intervals spanning seven semitones. Eleven of these are perfect fifths (P5), while the twelfth is a diminished sixth (d6). Since they span the same number of semitones, P5 and d6 are considered to be enharmonically equivalent. In an equally
Equal temperament
An equal temperament is a musical temperament, or a system of tuning, in which every pair of adjacent notes has an identical frequency ratio. As pitch is perceived roughly as the logarithm of frequency, this means that the perceived "distance" from every note to its nearest neighbor is the same for...
tuned chromatic scale, P5 and d6 have exactly the same size. The same is true for all the enharmonically equivalent intervals spanning 4 semitones (M3 and d4), or 3 semitones (m3 and A2). However, in the meantone temperament this is not true. In this tuning system, enharmonically equivalent intervals may have different sizes, and some intervals may markedly deviate from their justly tuned
Just intonation
In music, just intonation is any musical tuning in which the frequencies of notes are related by ratios of small whole numbers. Any interval tuned in this way is called a just interval. The two notes in any just interval are members of the same harmonic series...
ideal ratios. As explained in the previous section, if the deviation is too large, then the given interval is not usable, either by itself or in a chord.
The following table focuses only on the above-mentioned three interval types, used to form major and minor triads. Each row shows three intervals of different types but which have the same root note. Each interval is specified by a pair of notes. To the right of each interval is listed the formula for the interval ratio
Interval ratio
In music, an interval ratio is a ratio of the frequencies of the pitches in a musical interval. For example, a just perfect fifth is 3:2 , 1.5, and may be approximated by an equal tempered perfect fifth which is 27/12, 1.498...
. The intervals d4, d6 and A2 may be regarded as wolf interval
Wolf interval
In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament...
s, and have been marked in red
Red
Red is any of a number of similar colors evoked by light consisting predominantly of the longest wavelengths of light discernible by the human eye, in the wavelength range of roughly 630–740 nm. Longer wavelengths than this are called infrared , and cannot be seen by the naked eye...
. S and X denote the ratio of the two above-mentioned kinds of semitones (m2 and A1).
| 3 semitones (m3 or A2) |
4 semitones (M3 or d4) |
7 semitones (P5 or d6) |
|||
|---|---|---|---|---|---|
| Interval | Ratio | Interval | Ratio | Interval | Ratio |
| C—E | S2 · X | C—E | S2 · X2 | C—G | S4 · X3 |
| C—E | S2 · X | C—F | S3 · X | C—G | S4 · X3 |
| D—F | S2 · X | D—F | S2 · X2 | D—A | S4 · X3 |
| E—F | S · X2 | E—G | S2 · X2 | E—B | S4 · X3 |
| E—G | S2 · X | E—G | S2 · X2 | E—B | S4 · X3 |
| F—G | S · X2 | F—A | S2 · X2 | F—C | S4 · X3 |
| F—A | S2 · X | F—B | S3 · X | F—C | S4 · X3 |
| G—B | S2 · X | G—B | S2 · X2 | G—D | S4 · X3 |
| G—B | S2 · X | G—C | S3 · X | G—E | S5 · X2 |
| A—C | S2 · X | A—C | S2 · X2 | A—E | S4 · X3 |
| B—C | S · X2 | B—D | S2 · X2 | B—F | S4 · X3 |
| B—D | S2 · X | B—E | S3 · X | B—F | S4 · X3 |
First, look at the last two columns on the right. All the 7-semitone intervals except one have a ratio of
which deviates by −5.4 cents from the just 3:2 of 702.0 cents. Five cents is small and acceptable. On the other hand, the d6 from G to E has a ratio of
which deviates by +35.7 cents from the just fifth. Thirty-five cents is beyond the acceptable range.
Now look at the two columns in the middle. Eight of the twelve 4-semitone intervals have a ratio of
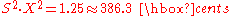
which is exactly a just 5:4. On the other hand, the four d4 with roots at C, F, G and B have a ratio of
which deviates by +41.1 cents from the just M3. Again, this sounds badly out of tune.
Major triads are formed out of both major thirds and perfect fifths. If either of the two intervals is substituted by a wolf interval (d6 instead of P5, or d4 instead of M3), then the triad is not acceptable. Therefore major triads with root notes of C, F, G and B are not used in meantone scales whose fundamental note is C.
Now look at the first two columns on the left. Nine of the twelve 3-semitone intervals have a ratio of
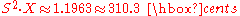
which deviates by −5.4 cents from the just 6:5 of 315.6 cents. Five cents is acceptable. On the other hand, the three augmented seconds whose roots are E, F and B have a ratio of
which deviates by −46.4 cents from the just minor third. It is a close match, however, for the 7:6 septimal minor third
Septimal minor third
In music, the septimal minor third , also called the subminor third, is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5...
of 266.9 cents, deviating by +2.3 cents. These augmented seconds, though sufficiently consonant by themselves, will sound "exotic" or atypical when plaied together with a perfect fifth.
Minor triads are formed out of both minor thirds and fifths. If either of the two intervals are substituted by an enharmonically equivalent interval (d6 instead of P5, or A2 instead of m3), then the triad will not sound good. Therefore minor triads with root notes of E, F, G and B are not used in the meantone scale defined above.
The following major triads are usable: C, D, E, E, F, G, A, B.
The following minor triads are usable: C, C, D, E, F, G, A, B.
The following root notes are useful for both major and minor triads: C, D, E, G and A. Notice that these five pitches form a major pentatonic scale
Pentatonic scale
A pentatonic scale is a musical scale with five notes per octave in contrast to a heptatonic scale such as the major scale and minor scale...
.
The following root notes are useful only for major triads: E, F, B.
The following root notes are useful only for minor triads: C, F, B.
The following root note is useful for neither major nor minor triad: G.
Alternative construction
As discussed above, in the quarter-comma meantone temperament,- the ratio of a greater (diatonic) semitone is
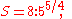
- the ratio of a lesser (chromatic) semitone is
- the ratio of most whole tones is
- the ratio of most fifths is
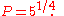
It can be verified through calculation that most whole tones (namely, the major seconds) are composed of one greater and one lesser semitone:
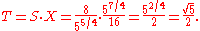
Similarly, a fifth is typically composed of three tones and one greater semitone:
which is equivalent to four greater and three lesser semitones:
Diatonic scale
A diatonic scaleDiatonic scale
In music theory, a diatonic scale is a seven note, octave-repeating musical scale comprising five whole steps and two half steps for each octave, in which the two half steps are separated from each other by either two or three whole steps...
can be constructed by starting from the fundamental note and multiplying it either by T to move up by a tone or by S to move up by a semitone.
C D E F G A B C'
|----|----|----|----|----|----|----|
T T S T T T S
The resulting interval sizes with respect to the base note C are shown in the following table:
| Note | Formula | Ratio | Cents | Pythagorean cents |
EQT Cents |
|---|---|---|---|---|---|
| C | 1 | 1.0000 | 0.0 | 0.0 | 0 |
| D | T | 1.1180 | 193.2 | 203.9 | 200 |
| E | T 2 | 1.2500 | 386.3 | 407.8 | 400 |
| F | T 2 S | 1.3375 | 503.4 | 498.0 | 500 |
| G | P | 1.4953 | 696.6 | 702.0 | 700 |
| A | P T | 1.6719 | 889.7 | 905.9 | 900 |
| B | P T 2 | 1.8692 | 1082.9 | 1109.8 | 1100 |
| C' | P T 2 S | 2.0000 | 1200.0 | 1200.0 | 1200 |
Chromatic scale
Construction of a 1/4-comma meantone chromatic scaleChromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
can proceed by stacking a series of 12 semitones, each of which may be either diatonic (S) or chromatic (X).
C C D E E F F G G A B B C'
|----|----|----|----|----|----|----|----|----|----|----|----|
X S S X S X S X S S X S
Notice that this scale is an extension of the diatonic scale shown in the previous table. Only five notes have been added: C, E, F, G and B (a pentatonic scale
Pentatonic scale
A pentatonic scale is a musical scale with five notes per octave in contrast to a heptatonic scale such as the major scale and minor scale...
).
As explained above, an identical scale was originally defined and produced by using a sequence of tempered fifths, ranging from E (five fifths below D) to G (six fifths above D), rather than a sequence of semitones. This more conventional approach, similar to the D-based Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
system, explains the reason why the X and S semitones are arranged in the particular and apparently arbitrary sequence shown above.
The interval sizes with respect to the base note C are presented in the following table. The frequency ratios are computed as shown by the formulas. Delta is the difference in cents between meantone and 12-TET. 1/4-c is the difference in quarter-commas between meantone and Pythagorean tuning.
| Note | Formula | Ratio | Cents | 12TET | Delta | 1/4-c |
|---|---|---|---|---|---|---|
| C | 1 | 1.0000 | 0.0 | 0 | 0.0 | 0 |
| C | X | 1.0449 | 76.0 | 100 | −24.0 | −7 |
| D | T | 1.1180 | 193.2 | 200 | −6.8 | −2 |
| E | T S | 1.1963 | 310.3 | 300 | +10.3 | 3 |
| E | T 2 | 1.2500 | 386.3 | 400 | −13.7 | −4 |
| F | T 2 S | 1.3375 | 503.4 | 500 | +3.4 | 1 |
| F | T 3 | 1.3975 | 579.5 | 600 | −20.5 | −6 |
| G | P | 1.4953 | 696.6 | 700 | −3.4 | −1 |
| G | P X | 1.5625 | 772.6 | 800 | −27.4 | −8 |
| A | P T | 1.6719 | 889.7 | 900 | −10.3 | −3 |
| B | P T S | 1.7889 | 1006.8 | 1000 | +6.8 | 2 |
| B | P T 2 | 1.8692 | 1082.9 | 1100 | −17.1 | −5 |
| C' | P T 2 S | 2.0000 | 1200.0 | 1200 | 0.0 | 0 |
Comparison with 31 equal temperament
The perfect fifth of quarter-comma meantone, expressed as a fraction of an octave, is 1/4 log2 5. This number is irrationalIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
and in fact transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
; hence a chain of meantone fifths, like a chain of pure 3/2 fifths, never closes (i.e. never equals a chain of octaves). However, the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
approximations to this irrational fraction number allow us to find equal divisions of the octave which do close; the denominators of these are 1, 2, 5, 7, 12, 19, 31, 174, 205, 789 ... From this we find that 31 quarter-comma meantone fifths come close to closing, and conversely 31 equal temperament
31 equal temperament
In music, 31 equal temperament, 31-ET, which can also be abbreviated 31-TET, 31-EDO , , is the tempered scale derived by dividing the octave into 31 equal-sized steps...
represents a good approximation to quarter-comma meantone. See: schisma
Schisma
In music, the schisma is the ratio between a Pythagorean comma and a syntonic comma and equals 32805:32768, which is 1.9537 cents...
.