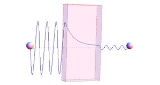
Quantum tunnelling
Encyclopedia
Quantum tunnelling refers to the quantum mechanical
phenomenon where a particle tunnels through a barrier that it classically
could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important applications to modern devices such as the tunnel diode
. The effect was predicted in the early 20th century, and its acceptance as a general, physical phenomenon came mid-century.
As a consequence of the wave–particle duality
of matter, tunnelling is often explained using the Heisenberg uncertainty principle. Purely quantum mechanical concepts are central to the phenomenon, so quantum tunnelling is one of the defining features of quantum mechanics and the particle–wave duality of matter.
. It was examined further by Marie
and Pierre Curie
, for which they earned the Nobel Prize in Physics
. Ernest Rutherford
and Egon Schweidler
studied its nature, which was later verified empirically by Friedrich Kohlrausch
. The idea of the half-life
and the impossibility of predicting decay was created from their work.
Friedrich Hund
was the first to take notice of tunnelling in 1927 when he was calculating the ground state of the double-well potential. Its first application was a mathematical explanation for alpha decay
, which was done in 1928 by George Gamow
and independently by Ronald Gurney
and Edward Condon
. The two researchers simultaneously solved the Schrödinger equation
for a model nuclear potential and derived a relationship between the half-life
of the particle and the energy of emission that depended directly on the mathematical probability of tunnelling.
After attending a seminar by Gamow, Max Born
recognized the generality of tunnelling. He realized that it was not restricted to nuclear physics
, but was a general result of quantum mechanics
that applies to many different systems. Shortly thereafter, both groups considered the case of particles tunnelling into the nucleus. The study of semiconductor
s and the development of transistor
s and diode
s led to the acceptance of electron tunnelling in solids by 1957. The work of Ivar Giaever
and Brian David Josephson
led to the BCS theory
of superconductivity
and the prediction of supercurrent
s.
Please refer to http://www.worldscibooks.com/etextbook/4984/4984_chap1.pdf for a more accurate history.
, the study of what happens at the quantum scale. This process cannot be directly perceived, so much of its understanding is shaped by the macroscopic world, which classical mechanics
can adequately explain. Particles in that realm are understood to travel between potential barriers as a ball rolls over a hill; if the ball does not have enough energy to surmount the hill, it comes back down. The two forms of mechanics differ in their treatment of this scenario. Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier will not be able to reach the other side. In quantum mechanics, these particles can, with a very small probability, tunnel to the other side, thus crossing the barrier.
The reason for this difference comes from the treatment of matter in quantum mechanics as having properties of waves and particles
. One interpretation of this duality involves the Heisenberg uncertainty principle, which defines a limit on how precisely the position and the momentum
of a particle can be known at the same time. This implies that there are no solutions with a probability of exactly zero (or one), though said solution may approach infinity. Hence, the probability of a given particle's existence on the opposite side of an intervening barrier is non-zero, and such particles will appear—with no indication of physically transiting the barrier—on the 'other' (a semantically difficult word in this instance) side with a frequency proportional to this probability.
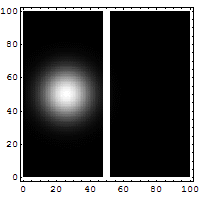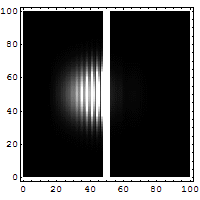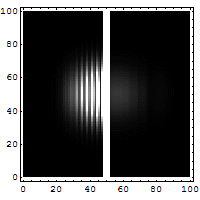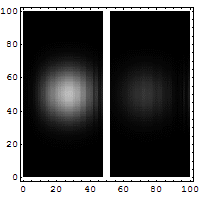
. Therefore, problems in quantum mechanics center around the analysis of the wave function for a system. Using mathematical formulations of quantum mechanics, such as the Schrödinger equation
, the wave function can be solved. This is directly related to the probability density of the particle's position, which describes the probability that the particle is at any given place. In the limit of large barriers, the probability of tunnelling decreases for taller and wider barriers.
For simple tunnelling-barrier models, such as the rectangular barrier, an analytic solution exists. Problems in real life often do not have one, so "semiclassical" or "quasiclassical" methods have been developed to give approximate solutions to these problems, like the WKB approximation
. Probabilities may be derived with arbitrary precision, constrained by computational resources, via Feynman
's path integral
method; such precision is seldom required in engineering practice.
to light
) and the application of the non-dispersive wave-equation
from acoustics
applied to "waves on strings". Evanescent wave coupling, until recently, was only called "tunnelling" in quantum mechanics; now it is used in other contexts.
These effects are modelled similarly to the rectangular potential barrier. In these cases, there is one transmission medium
through which the wave propagates
that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential
solutions in medium B.
In optics
, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle's total energy is greater than its potential energy
and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete; approximations are useful in this case.
(VLSI) electronics and results in the substantial power drain and heating effects that plague high-speed and mobile technology; it is considered the lower limit on how small computer chips can be made.
). This was the first application of quantum tunnelling and led to the first approximations.
, where electrons randomly jump from the surface of a metal to follow a voltage bias because they statistically end up with more energy than the barrier, through random collisions with other particles. When the electric field is very large, the barrier becomes thin enough for electrons to tunnel out of the atomic state, leading to a current that varies approximately exponentially with the electric field. These materials are important for flash memory
and for some electron microscopes.
. This has applications in precision measurements of voltages and magnetic fields, as well as the multijunction solar cell.
s are electrical semiconductor device
s that allow electric current
flow in one direction more than the other. The device depends on a depletion layer between N-type
and P-type semiconductor
s to serve its purpose; when these are very heavily doped the depletion layer can be thin enough for tunnelling. Then, when a small forward bias is applied the current due to tunnelling is significant. This has a maximum at the point where the voltage bias is such that the energy level of the p and n conduction band
s are the same. As the voltage bias is increased, the two conduction bands no longer line up and the diode acts typically.
Because the tunnelling current drops off rapidly, tunnel diodes can be created that have a range of voltages for which current decreases as voltage is increased. This peculiar property is used in some applications, like high speed devices where the characteristic tunnelling probability changes as rapidly as the bias voltage.
The resonant tunnelling diode
makes use of quantum tunnelling in a very different manner to achieve a similar result. This diode has a resonant voltage for which there is a lot of current that favors a particular voltage, achieved by placing two very thin layers with a high energy conductance band very near each other. This creates a quantum potential well
that has a discrete lowest energy level
. When this energy level is higher than that of the electrons, no tunnelling will occur, and the diode is in reverse bias. Once the voltage two energies align, the electrons flow like an open wire. As the voltage is increased further tunnelling becomes improbable and the diode acts like a normal diode again before a second energy level becomes noticeable.
of electrical conductivity makes excellent predictions about the nature of electrons conducting in metals, it can be furthered by using quantum tunnelling to explain the nature of the electron's collisions. When a free electron wave packet encounters a long array of uniformly spaced barriers the reflected part of the wave packet interferes uniformly with the transmitted one between all barriers so that there are cases of 100% transmission. The theory predicts that if positively charged nuclei form a perfectly rectangular array, electrons will tunnel through the metal as free electrons, leading to an extremely high conductance
, and that impurities in the metal will disrupt it significantly.
and Heinrich Rohrer
, allows imaging of individual atoms on the surface of a metal. It operates by taking advantage of the relationship between quantum tunnelling with distance. When the tip of the STM's needle is brought very close to a conduction surface that has a voltage bias, by measuring the current of electrons that are tunnelling between the needle and the surface, the distance between the needle and the surface can be measured. By using piezoelectric rods
that change in size when voltage is applied over them the height of the tip can be adjusted to keep the tunnelling current constant. The time-varying voltages that are applied to these rods can be recorded and used to image the surface of the conductor. STMs are accurate to 0.001 nm, or about 1% of atomic diameter.
can be written as
or
where
is the reduced Planck's constant, m is the particle mass, x represents distance measured in the direction of motion of the particle, Ψ is the Schrödinger wave function, V is the potential energy
of the particle (measured relative to any convenient reference level), E is the energy of the particle that is associated with motion in the x-axis (measured relative to V), and M(x) is a quantity defined by V(x) - E which has no accepted name in physics.
The solutions of the Schrödinger equation take different forms for different values of x, depending on whether M(x) is positive or negative. When M(x) is constant and negative, then the Schrödinger equation can be written in the form
The solutions of this equation represent traveling waves, with phase-constant +k or -k.
Alternatively, if M(x) is constant and positive, then the Schrödinger equation can be written in the form
The solutions of this equation are rising and falling exponentials in the form of evanescent wave
s.
When M(x) varies with position, the same difference in behaviour occurs, depending on whether M(x) is negative or positive. It follows that the sign of M(x) determines the nature of the medium, with positive M(x) corresponding to medium A as described above and negative M(x) corresponding to medium B. It thus follows that evanescent wave coupling can occur if a region of positive M(x) is sandwiched between two regions of negative M(x), hence creating a potential barrier.
The mathematics of dealing with the situation where M(x) varies with x is difficult, except in special cases that usually do not correspond to physical reality. A discussion of the semi-classical approximate method, as found in physics textbooks, is given in the next section. A full and complicated mathematical treatment appears in the 1965 monograph by Fröman and Fröman noted below. Their ideas have not been incorporated into physics textbooks, but their corrections have little quantitative effect.
, where 
is then separated into real and imaginary parts:
, where A(x) and B(x) are real-valued functions.
Substituting the second equation into the first and using the fact that the imaginary part needs to be 0 results in:
.
To solve this equation using the semiclassical approximation, each function must be expanded as a power series in
. From the equations, the power series must start with at least an order of 
to satisfy the real part of the equation; for a good classical limit starting with the highest a power of Planck's constant possible is preferable, which leads to
and
,
with the following constraints on the lowest order terms,
and
.
At this point two extreme cases can be considered.
Case 1
If the amplitude varies slowly as compared to the phase
and
Case 2
In both cases it is apparent from the denominator that both these approximate solutions are bad near the classical turning points
. Away from the potential hill, the particle acts similar to a free and oscillating wave; beneath the potential hill, the particle undergoes exponential changes in amplitude. By considering the behaviour at these limits and classical turning points a global solution can be made.
To start, choose a classical turning point,
and expand 
in a power series about 
:
Keeping only the first order term ensures linearity:
.
Using this approximation, the equation near
becomes a differential equation
:
.
This can be solved using Airy function
s as solutions.
Taking these solutions for all classical turning points, a global solution can be formed that links the limiting solutions. Given the 2 coefficients on one side of a classical turning point, the 2 coefficients on the other side of a classical turning point can be determined by using this local solution to connect them.
Hence, the Airy function solutions will asymptote into sine, cosine and exponential functions in the proper limits. The relationships between
and 
are
and
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunnelling through a single potential barrier is
,
where
are the 2 classical turning points for the potential barrier.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
phenomenon where a particle tunnels through a barrier that it classically
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
could not surmount. This plays an essential role in several physical phenomena, such as the nuclear fusion that occurs in main sequence stars like the sun, and has important applications to modern devices such as the tunnel diode
Tunnel diode
A tunnel diode or Esaki diode is a type of semiconductor diode which is capable of very fast operation, well into the microwave frequency region, by using quantum mechanical effects....
. The effect was predicted in the early 20th century, and its acceptance as a general, physical phenomenon came mid-century.
As a consequence of the wave–particle duality
Wave–particle duality
Wave–particle duality postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale objects...
of matter, tunnelling is often explained using the Heisenberg uncertainty principle. Purely quantum mechanical concepts are central to the phenomenon, so quantum tunnelling is one of the defining features of quantum mechanics and the particle–wave duality of matter.
History
Quantum tunnelling was developed from the study of radioactivity, which was discovered in 1896 by Henri BecquerelHenri Becquerel
Antoine Henri Becquerel was a French physicist, Nobel laureate, and the discoverer of radioactivity along with Marie Curie and Pierre Curie, for which all three won the 1903 Nobel Prize in Physics.-Early life:...
. It was examined further by Marie
Marie Curie
Marie Skłodowska-Curie was a physicist and chemist famous for her pioneering research on radioactivity. She was the first person honored with two Nobel Prizes—in physics and chemistry...
and Pierre Curie
Pierre Curie
Pierre Curie was a French physicist, a pioneer in crystallography, magnetism, piezoelectricity and radioactivity, and Nobel laureate. He was the son of Dr. Eugène Curie and Sophie-Claire Depouilly Curie ...
, for which they earned the Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
. Ernest Rutherford
Ernest Rutherford
Ernest Rutherford, 1st Baron Rutherford of Nelson OM, FRS was a New Zealand-born British chemist and physicist who became known as the father of nuclear physics...
and Egon Schweidler
Egon Schweidler
Egon Schweidler, was an Austrian physicist.-Biography:He was born in 1873 as the son of the court and Gerichtsadvokaten Emil von Schweidler born in Vienna. After studying physics and mathematics, he earned his doctorate with a dissertation "On the internal friction of mercury and some Amalgamen"...
studied its nature, which was later verified empirically by Friedrich Kohlrausch
Friedrich Kohlrausch
Friedrich Wilhelm Georg Kohlrausch was a German physicist who investigated the conductive properties of electrolytes and contributed to knowledge of their behaviour...
. The idea of the half-life
Half-life
Half-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to...
and the impossibility of predicting decay was created from their work.
Friedrich Hund
Friedrich Hund
Friedrich Hermann Hund was a German physicist from Karlsruhe known for his work on atoms and molecules.Hund worked at the Universities of Rostock, Leipzig, Jena, Frankfurt am Main, and Göttingen....
was the first to take notice of tunnelling in 1927 when he was calculating the ground state of the double-well potential. Its first application was a mathematical explanation for alpha decay
Alpha decay
Alpha decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle and thereby transforms into an atom with a mass number 4 less and atomic number 2 less...
, which was done in 1928 by George Gamow
George Gamow
George Gamow , born Georgiy Antonovich Gamov , was a Russian-born theoretical physicist and cosmologist. He discovered alpha decay via quantum tunneling and worked on radioactive decay of the atomic nucleus, star formation, stellar nucleosynthesis, Big Bang nucleosynthesis, cosmic microwave...
and independently by Ronald Gurney
Ronald Wilfried Gurney
Ronald Wilfred Gurney was a British theoretical physicist and research pupil of William Lawrence Bragg at the Victoria University of Manchester during the 1920s and 30s, Bristol University during the 1930s and later in the USA where he died.-Radioactive decay processes:Whilst at the Palmer...
and Edward Condon
Edward Condon
Edward Uhler Condon was a distinguished American nuclear physicist, a pioneer in quantum mechanics, and a participant in the development of radar and nuclear weapons during World War II.-Early life and career:...
. The two researchers simultaneously solved the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for a model nuclear potential and derived a relationship between the half-life
Half-life
Half-life, abbreviated t½, is the period of time it takes for the amount of a substance undergoing decay to decrease by half. The name was originally used to describe a characteristic of unstable atoms , but it may apply to any quantity which follows a set-rate decay.The original term, dating to...
of the particle and the energy of emission that depended directly on the mathematical probability of tunnelling.
After attending a seminar by Gamow, Max Born
Max Born
Max Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
recognized the generality of tunnelling. He realized that it was not restricted to nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
, but was a general result of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
that applies to many different systems. Shortly thereafter, both groups considered the case of particles tunnelling into the nucleus. The study of semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s and the development of transistor
Transistor
A transistor is a semiconductor device used to amplify and switch electronic signals and power. It is composed of a semiconductor material with at least three terminals for connection to an external circuit. A voltage or current applied to one pair of the transistor's terminals changes the current...
s and diode
Diode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
s led to the acceptance of electron tunnelling in solids by 1957. The work of Ivar Giaever
Ivar Giaever
Ivar Giaever is a physicist who shared the Nobel Prize in Physics in 1973 with Leo Esaki and Brian Josephson "for their discoveries regarding tunnelling phenomena in solids". Giaever's share of the prize was specifically for his "experimental discoveries regarding tunnelling phenomena in ......
and Brian David Josephson
Brian David Josephson
Brian David Josephson, FRS is a Welsh physicist. He became a Nobel Prize laureate in 1973 for the prediction of the eponymous Josephson effect....
led to the BCS theory
BCS theory
BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...
of superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
and the prediction of supercurrent
Supercurrent
A supercurrent is a superconducting current, that is, electric current which flows without dissipation....
s.
Please refer to http://www.worldscibooks.com/etextbook/4984/4984_chap1.pdf for a more accurate history.
Introduction to the concept
Quantum tunnelling is in the domain of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the study of what happens at the quantum scale. This process cannot be directly perceived, so much of its understanding is shaped by the macroscopic world, which classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
can adequately explain. Particles in that realm are understood to travel between potential barriers as a ball rolls over a hill; if the ball does not have enough energy to surmount the hill, it comes back down. The two forms of mechanics differ in their treatment of this scenario. Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier will not be able to reach the other side. In quantum mechanics, these particles can, with a very small probability, tunnel to the other side, thus crossing the barrier.
The reason for this difference comes from the treatment of matter in quantum mechanics as having properties of waves and particles
Wave–particle duality
Wave–particle duality postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale objects...
. One interpretation of this duality involves the Heisenberg uncertainty principle, which defines a limit on how precisely the position and the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of a particle can be known at the same time. This implies that there are no solutions with a probability of exactly zero (or one), though said solution may approach infinity. Hence, the probability of a given particle's existence on the opposite side of an intervening barrier is non-zero, and such particles will appear—with no indication of physically transiting the barrier—on the 'other' (a semantically difficult word in this instance) side with a frequency proportional to this probability.
The tunnelling problem
The wave function of a particle summarizes everything that can be known about a physical systemPhysical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
. Therefore, problems in quantum mechanics center around the analysis of the wave function for a system. Using mathematical formulations of quantum mechanics, such as the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, the wave function can be solved. This is directly related to the probability density of the particle's position, which describes the probability that the particle is at any given place. In the limit of large barriers, the probability of tunnelling decreases for taller and wider barriers.
For simple tunnelling-barrier models, such as the rectangular barrier, an analytic solution exists. Problems in real life often do not have one, so "semiclassical" or "quasiclassical" methods have been developed to give approximate solutions to these problems, like the WKB approximation
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
. Probabilities may be derived with arbitrary precision, constrained by computational resources, via Feynman
Feynman
Feynman may refer to:* Richard Feynman , physicist** Feynman diagram** Feynman graph** Feynman–Kac formula** The Feynman Lectures on Physics** Feynman integral, see Path integral formulation** Feynman parametrization...
's path integral
Path integral
Path integral may refer to:* Line integral, the integral of a function along a curve* Functional integration, the integral of a functional over a space of curves...
method; such precision is seldom required in engineering practice.
Related phenomena
There are several phenomena that have the same behavior as quantum tunnelling, and thus can be accurately described by tunnelling. Examples include the evanescent wave coupling (the application of Maxwell's wave-equationMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
to light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
) and the application of the non-dispersive wave-equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
from acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
applied to "waves on strings". Evanescent wave coupling, until recently, was only called "tunnelling" in quantum mechanics; now it is used in other contexts.
These effects are modelled similarly to the rectangular potential barrier. In these cases, there is one transmission medium
Transmission medium
A transmission medium is a material substance that can propagate energy waves...
through which the wave propagates
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
solutions in medium B.
In optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle's total energy is greater than its potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete; approximations are useful in this case.
Applications
Tunnelling occurs with barriers of thickness around 1-3 nm and smaller, but is the cause of some important macroscopic physical phenomena. For instance, tunnelling is a source of current leakage in very-large-scale integrationVery-large-scale integration
Very-large-scale integration is the process of creating integrated circuits by combining thousands of transistors into a single chip. VLSI began in the 1970s when complex semiconductor and communication technologies were being developed. The microprocessor is a VLSI device.The first semiconductor...
(VLSI) electronics and results in the substantial power drain and heating effects that plague high-speed and mobile technology; it is considered the lower limit on how small computer chips can be made.
Radioactive decay
Radioactive decay is the process of emission of particles and energy from the unstable nucleus of an atom to form a stable product. This is done via the tunnelling of a particle out of the nucleus (an electron tunnelling into the nucleus is electron captureElectron capture
Electron capture is a process in which a proton-rich nuclide absorbs an inner atomic electron and simultaneously emits a neutrino...
). This was the first application of quantum tunnelling and led to the first approximations.
Cold emission
Cold emission of electrons is relevant to semiconductors and superconductor physics. It is similar to thermionic emissionThermionic emission
Thermionic emission is the heat-induced flow of charge carriers from a surface or over a potential-energy barrier. This occurs because the thermal energy given to the carrier overcomes the binding potential, also known as work function of the metal. The charge carriers can be electrons or ions, and...
, where electrons randomly jump from the surface of a metal to follow a voltage bias because they statistically end up with more energy than the barrier, through random collisions with other particles. When the electric field is very large, the barrier becomes thin enough for electrons to tunnel out of the atomic state, leading to a current that varies approximately exponentially with the electric field. These materials are important for flash memory
Flash memory
Flash memory is a non-volatile computer storage chip that can be electrically erased and reprogrammed. It was developed from EEPROM and must be erased in fairly large blocks before these can be rewritten with new data...
and for some electron microscopes.
Tunnel junction
A simple barrier can be created by separating two conductors with a very thin insulator. These are tunnel junctions, the study of which requires quantum tunnelling. Josephson junctions take advantage of quantum tunnelling and the superconductivity of some semiconductors to create the Josephson effectJosephson effect
The Josephson effect is the phenomenon of supercurrent across two superconductors coupled by a weak link...
. This has applications in precision measurements of voltages and magnetic fields, as well as the multijunction solar cell.
Tunnel diode
DiodeDiode
In electronics, a diode is a type of two-terminal electronic component with a nonlinear current–voltage characteristic. A semiconductor diode, the most common type today, is a crystalline piece of semiconductor material connected to two electrical terminals...
s are electrical semiconductor device
Semiconductor device
Semiconductor devices are electronic components that exploit the electronic properties of semiconductor materials, principally silicon, germanium, and gallium arsenide, as well as organic semiconductors. Semiconductor devices have replaced thermionic devices in most applications...
s that allow electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
flow in one direction more than the other. The device depends on a depletion layer between N-type
N-type semiconductor
N-type semiconductors are a type of extrinsic semiconductor where the dopant atoms are capable of providing extra conduction electrons to the host material . This creates an excess of negative electron charge carriers....
and P-type semiconductor
P-type semiconductor
A P-type semiconductor is obtained by carrying out a process of doping: that is, adding a certain type of atoms to the semiconductor in order to increase the number of free charge carriers ....
s to serve its purpose; when these are very heavily doped the depletion layer can be thin enough for tunnelling. Then, when a small forward bias is applied the current due to tunnelling is significant. This has a maximum at the point where the voltage bias is such that the energy level of the p and n conduction band
Conduction band
In the solid-state physics field of semiconductors and insulators, the conduction band is the range of electron energies, higher than that of the valence band, sufficient to free an electron from binding with its individual atom and allow it to move freely within the atomic lattice of the material...
s are the same. As the voltage bias is increased, the two conduction bands no longer line up and the diode acts typically.
Because the tunnelling current drops off rapidly, tunnel diodes can be created that have a range of voltages for which current decreases as voltage is increased. This peculiar property is used in some applications, like high speed devices where the characteristic tunnelling probability changes as rapidly as the bias voltage.
The resonant tunnelling diode
Resonant tunnelling diode
Resonant-tunneling diode is a diode with a resonant-tunneling structure in which electrons can tunnel through some resonant states at certain energy levels...
makes use of quantum tunnelling in a very different manner to achieve a similar result. This diode has a resonant voltage for which there is a lot of current that favors a particular voltage, achieved by placing two very thin layers with a high energy conductance band very near each other. This creates a quantum potential well
Potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
that has a discrete lowest energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
. When this energy level is higher than that of the electrons, no tunnelling will occur, and the diode is in reverse bias. Once the voltage two energies align, the electrons flow like an open wire. As the voltage is increased further tunnelling becomes improbable and the diode acts like a normal diode again before a second energy level becomes noticeable.
Quantum conductivity
While the Drude modelDrude model
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials...
of electrical conductivity makes excellent predictions about the nature of electrons conducting in metals, it can be furthered by using quantum tunnelling to explain the nature of the electron's collisions. When a free electron wave packet encounters a long array of uniformly spaced barriers the reflected part of the wave packet interferes uniformly with the transmitted one between all barriers so that there are cases of 100% transmission. The theory predicts that if positively charged nuclei form a perfectly rectangular array, electrons will tunnel through the metal as free electrons, leading to an extremely high conductance
Conductance
Conductance may refer to:* Electrical conductance, the ability for electricity to flow a certain path* Fluid conductance, the ability for fluid to transmit through materials* Thermal conductivity, the ability for temperatures to transmit through materials...
, and that impurities in the metal will disrupt it significantly.
Scanning tunnelling microscope
The scanning tunnelling microscope (STM), invented by Gerd BinnigGerd Binnig
Gerd Binnig is a German physicist, and a Nobel laureate.He was born in Frankfurt am Main and played in the ruins of the city during his childhood. His family lived partly in Frankfurt and partly in Offenbach am Main, and he attended school in both cities. At the age of 10, he decided to become a...
and Heinrich Rohrer
Heinrich Rohrer
Heinrich Rohrer is a Swiss physicist who shared half of the 1986 Nobel Prize in Physics with Gerd Binnig for the design of the scanning tunneling microscope .-Biography:...
, allows imaging of individual atoms on the surface of a metal. It operates by taking advantage of the relationship between quantum tunnelling with distance. When the tip of the STM's needle is brought very close to a conduction surface that has a voltage bias, by measuring the current of electrons that are tunnelling between the needle and the surface, the distance between the needle and the surface can be measured. By using piezoelectric rods
Piezoelectric sensor
A piezoelectric sensor is a device that uses the piezoelectric effect to measure pressure, acceleration, strain or force by converting them to an electrical charge.-Applications:...
that change in size when voltage is applied over them the height of the tip can be adjusted to keep the tunnelling current constant. The time-varying voltages that are applied to these rods can be recorded and used to image the surface of the conductor. STMs are accurate to 0.001 nm, or about 1% of atomic diameter.
Faster than Light
It is possible for spin zero particles to travel faster than c when tunnelling. This apparently violates the principle of causality, since there will be a frame of reference in which it arrives before it has left. However, careful analysis of the transmission of the wave packet shows that there is actually no violation of relativity theory. In 1991, P.E. Low reviewed the phenomenon, concluding that the apparent faster than light result results from a very narrow forerunner part of the wave packet.Mathematical discussions of quantum tunnelling
The following subsections discuss the mathematical formulations of quantum tunnelling.The Schrödinger equation
The time-independent Schrödinger equation for one particle in one dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
can be written as
orwhere
is the reduced Planck's constant, m is the particle mass, x represents distance measured in the direction of motion of the particle, Ψ is the Schrödinger wave function, V is the potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
of the particle (measured relative to any convenient reference level), E is the energy of the particle that is associated with motion in the x-axis (measured relative to V), and M(x) is a quantity defined by V(x) - E which has no accepted name in physics.
The solutions of the Schrödinger equation take different forms for different values of x, depending on whether M(x) is positive or negative. When M(x) is constant and negative, then the Schrödinger equation can be written in the form
The solutions of this equation represent traveling waves, with phase-constant +k or -k.
Alternatively, if M(x) is constant and positive, then the Schrödinger equation can be written in the form
The solutions of this equation are rising and falling exponentials in the form of evanescent wave
Evanescent wave
An evanescent wave is a nearfield standing wave with an intensity that exhibits exponential decay with distance from the boundary at which the wave was formed. Evanescent waves are a general property of wave-equations, and can in principle occur in any context to which a wave-equation applies...
s.
When M(x) varies with position, the same difference in behaviour occurs, depending on whether M(x) is negative or positive. It follows that the sign of M(x) determines the nature of the medium, with positive M(x) corresponding to medium A as described above and negative M(x) corresponding to medium B. It thus follows that evanescent wave coupling can occur if a region of positive M(x) is sandwiched between two regions of negative M(x), hence creating a potential barrier.
The mathematics of dealing with the situation where M(x) varies with x is difficult, except in special cases that usually do not correspond to physical reality. A discussion of the semi-classical approximate method, as found in physics textbooks, is given in the next section. A full and complicated mathematical treatment appears in the 1965 monograph by Fröman and Fröman noted below. Their ideas have not been incorporated into physics textbooks, but their corrections have little quantitative effect.
The WKB approximation
The wave function is expressed as the exponential of a function:, where is then separated into real and imaginary parts:, where A(x) and B(x) are real-valued functions.Substituting the second equation into the first and using the fact that the imaginary part needs to be 0 results in:
.To solve this equation using the semiclassical approximation, each function must be expanded as a power series in
. From the equations, the power series must start with at least an order of to satisfy the real part of the equation; for a good classical limit starting with the highest a power of Planck's constant possible is preferable, which leads toand
,with the following constraints on the lowest order terms,
and
.At this point two extreme cases can be considered.
Case 1
If the amplitude varies slowly as compared to the phase
and
- which corresponds to classical motion. Resolving the next order of expansion yields
Case 2
- If the phase varies slowly as compared to the amplitude,
and
- which corresponds to tunnelling. Resolving the next order of the expansion yields
In both cases it is apparent from the denominator that both these approximate solutions are bad near the classical turning points
. Away from the potential hill, the particle acts similar to a free and oscillating wave; beneath the potential hill, the particle undergoes exponential changes in amplitude. By considering the behaviour at these limits and classical turning points a global solution can be made.To start, choose a classical turning point,
and expand in a power series about :Keeping only the first order term ensures linearity:
.Using this approximation, the equation near
becomes a differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
:
.This can be solved using Airy function
Airy function
In the physical sciences, the Airy function Ai is a special function named after the British astronomer George Biddell Airy...
s as solutions.
Taking these solutions for all classical turning points, a global solution can be formed that links the limiting solutions. Given the 2 coefficients on one side of a classical turning point, the 2 coefficients on the other side of a classical turning point can be determined by using this local solution to connect them.
Hence, the Airy function solutions will asymptote into sine, cosine and exponential functions in the proper limits. The relationships between
and areand
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunnelling through a single potential barrier is
,where
are the 2 classical turning points for the potential barrier.See also
- Fowler-Nordheim tunnelling
- Dielectric Barrier DischargeDielectric barrier dischargeDielectric-barrier discharge is the electrical discharge between two electrodes separated by an insulating dielectric barrier. Originally called silent discharge and also known as ozone production discharge or partial discharge, it was first reported by Ernst Werner von Siemens in 1857.- Process...
- Holstein–Herring method