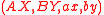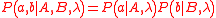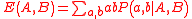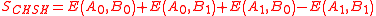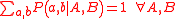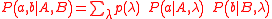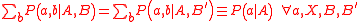Quantum nonlocality
Encyclopedia
Quantum nonlocality is the phenomenon by which measurements made at a microscopic level necessarily refute one or more notions (often referred to as local realism) that are regarded as intuitively true in classical mechanics
. Rigorously, quantum nonlocality refers to quantum mechanical
predictions of many-system measurement correlations that cannot be simulated by any local hidden variable theory
. Many entangled
quantum states produce such correlations when measured, as demonstrated by Bell's theorem
.
Experiments have generally favoured quantum mechanics as a description of nature, over local hidden variable theories. Any physical theory that supersedes or replaces quantum theory must make similar experimental predictions and must therefore also be nonlocal in this sense; quantum nonlocality is a property of the universe that is independent of our description of nature.
Whilst quantum nonlocality improves the efficiency of various computational tasks, it does not allow for faster-than-light communication, and hence is compatible with special relativity
. However, it prompts many of the foundational discussions concerning quantum theory. The study of physical theories more nonlocal than quantum theory - yet still compatible with special relativity - is an active field of research.
, situated in separate laboratories. They conduct a simple experiment in which Alice chooses and pushes one of two buttons, A0 and A1, on her apparatus, and Bob observes on his apparatus one of two indicating lamps, b0 and b1, lighting. In this case there are four possible events that could occur in the experiment: (A0,b0), (A0,b1), (A1,b0) and (A1,b1). Suppose that after many runs of the experiment, only the events (A0,b0) and (A1,b1) occur; this is good evidence that A has an influence on B. Indeed, Alice could easily send messages to Bob by encoding those messages into sequences of 0's and 1's, and causing the b0 or b1 lamp to light up respectively.
More realistically, suppose that the four events occur with (conditional) probabilities P(b0|A0), P(b1|A0) = 1 - P(b0|A0), P(b0|A1) and P(b1|A1) = 1 - P(b0|A1). Here P(b0|A0) is the probability that Bob's b0 lamp lit up, given that Alice pushed the button A0. We can still rigorize the notion that A has an influence on B in this setting: if P(b0|A0) differs from P(b0|A1) then Alice's choice of button still affects the probabilistic outcome on Bob's side, and it is still possible for Alice to send Bob messages with low probability of error. For example, if P(b0|A0) = and P(b0|A1) =
and P(b0|A1) =  , then after 100 runs of the experiment in which Alice pushed the same button, Bob can tell with high probability which button it was by looking at how often b0 occurred.
, then after 100 runs of the experiment in which Alice pushed the same button, Bob can tell with high probability which button it was by looking at how often b0 occurred.
Here is a more complicated scenario: Alice pushes one of two buttons, A0 and A1, and Bob also pushes one of two buttons, B0 and B1. Alice observes one of two outcomes, a0 and a1, and Bob also observes one of two outcomes, b0 and b1. There are 24 = 16 possible combinations of these 4 events:
where each of X,Y,x,y is 0 or 1.
Suppose that of these 16, only 8 combinations actually occur, with the following (conditional) probabilities:
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. Rigorously, quantum nonlocality refers to quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
predictions of many-system measurement correlations that cannot be simulated by any local hidden variable theory
Local hidden variable theory
In quantum mechanics, a local hidden variable theory is one in which distant events are assumed to have no instantaneous effect on local ones....
. Many entangled
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
quantum states produce such correlations when measured, as demonstrated by Bell's theorem
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
.
Experiments have generally favoured quantum mechanics as a description of nature, over local hidden variable theories. Any physical theory that supersedes or replaces quantum theory must make similar experimental predictions and must therefore also be nonlocal in this sense; quantum nonlocality is a property of the universe that is independent of our description of nature.
Whilst quantum nonlocality improves the efficiency of various computational tasks, it does not allow for faster-than-light communication, and hence is compatible with special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. However, it prompts many of the foundational discussions concerning quantum theory. The study of physical theories more nonlocal than quantum theory - yet still compatible with special relativity - is an active field of research.
Example
Imagine two experimentalists, Alice and BobAlice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
, situated in separate laboratories. They conduct a simple experiment in which Alice chooses and pushes one of two buttons, A0 and A1, on her apparatus, and Bob observes on his apparatus one of two indicating lamps, b0 and b1, lighting. In this case there are four possible events that could occur in the experiment: (A0,b0), (A0,b1), (A1,b0) and (A1,b1). Suppose that after many runs of the experiment, only the events (A0,b0) and (A1,b1) occur; this is good evidence that A has an influence on B. Indeed, Alice could easily send messages to Bob by encoding those messages into sequences of 0's and 1's, and causing the b0 or b1 lamp to light up respectively.
More realistically, suppose that the four events occur with (conditional) probabilities P(b0|A0), P(b1|A0) = 1 - P(b0|A0), P(b0|A1) and P(b1|A1) = 1 - P(b0|A1). Here P(b0|A0) is the probability that Bob's b0 lamp lit up, given that Alice pushed the button A0. We can still rigorize the notion that A has an influence on B in this setting: if P(b0|A0) differs from P(b0|A1) then Alice's choice of button still affects the probabilistic outcome on Bob's side, and it is still possible for Alice to send Bob messages with low probability of error. For example, if P(b0|A0) =
 and P(b0|A1) =
and P(b0|A1) =  , then after 100 runs of the experiment in which Alice pushed the same button, Bob can tell with high probability which button it was by looking at how often b0 occurred.
, then after 100 runs of the experiment in which Alice pushed the same button, Bob can tell with high probability which button it was by looking at how often b0 occurred.Here is a more complicated scenario: Alice pushes one of two buttons, A0 and A1, and Bob also pushes one of two buttons, B0 and B1. Alice observes one of two outcomes, a0 and a1, and Bob also observes one of two outcomes, b0 and b1. There are 24 = 16 possible combinations of these 4 events:
where each of X,Y,x,y is 0 or 1.
Suppose that of these 16, only 8 combinations actually occur, with the following (conditional) probabilities:
-
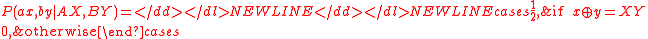
where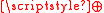 denotes addition modulo 2. Hence the two outcomes are perfectly anticorrelated (either (a0,b1) or (a1,b0), equiprobably) when (A1,B1) is chosen. In the three other cases ((A0,B0), (A0,B1), (A1,B0)), the two outcomes are perfectly correlated (either (a0,b0) or (a1,b1), equiprobably).
denotes addition modulo 2. Hence the two outcomes are perfectly anticorrelated (either (a0,b1) or (a1,b0), equiprobably) when (A1,B1) is chosen. In the three other cases ((A0,B0), (A0,B1), (A1,B0)), the two outcomes are perfectly correlated (either (a0,b0) or (a1,b1), equiprobably).
Do these outcomes imply that some influence exists (A on B, or B on A), or not? The question is important, since the answer depends on our fundamental assumptions about how mathematical theories describe physical reality.
On the one hand, Alice cannot send a message to Bob, using her buttons A0, A1 and his indicators b0, b1 (nor Bob to Alice). In this sense there is no influence of A on B, or of B on A, since it is easily checked that P(bx|A0) = P(bx|A1) for both x = 0 and x = 1 in the above example. That is to say, this particular set of probabilities is non-signalling.
On the other hand, it is provably impossible for two separated parties to simulate this outcome without any kind of interaction or communication between them. Thorough logical analysis reveals that the above outcome can only occur if there is some direct influence between A and B, if we assume local realism and, arguably, counterfactual definitenessCounterfactual definitenessIn some interpretations of quantum mechanics, counterfactual definiteness is the ability to speak with meaning of the definiteness of the results of measurements that have not been performed...
. These fundamental assumptions, deeply rooted in our physical intuition, are incompatible with quantum theory. Different interpretations of quantum mechanics reject different parts of local realism and/or counterfactual definiteness (for detail, see Principle of localityPrinciple of localityIn physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
). A classical definition of nonlocality, i.e. direct influence of one object on another, distant object, normally takes local realism and counterfactual definiteness for granted.
Einstein, Podolsky and Rosen
In 1935, EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
, Podolsky and Rosen published a thought experiment with which they hoped to expose the incompleteness of the Copenhagen interpretationCopenhagen interpretationThe Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
of quantum mechanics in relation to the violation of realism and local causalityPrinciple of localityIn physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
at the microscopic scale that it described. David BohmDavid BohmDavid Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
later modified the original EPR thought experiment, simplifying the mathematics and highlighting assumptions like locality (which Einstein et al had tacitly assumed). In Bohm's version of the experiment, a spin-zero particle decayParticle decayParticle decay is the spontaneous process of one elementary particle transforming into other elementary particles. During this process, an elementary particle becomes a different particle with less mass and an intermediate particle such as W boson in muon decay. The intermediate particle then...
s into two spin-half particles such that there is no interaction between the two particles after decay. The quantum state of the two particles prior to measurement can be written as
-

Here, subscripts A and B distinguish the two particles, though it is more convenient and usual to refer to these particles as being in the possession of two experimentalists called Alice and Bob. The rules of quantum theory give predictions for the outcomes of measurements performed by the experimentalists. Alice, for example, will measure her particle to be spin-up in an average of fifty percent of measurements. However, according to the Copenhagen interpretation, Alice's measurement causes the state of the two particles to collapse, so that if Alice measures spin-up in some direction n, the quantum state after measurement is the corresponding eigenstate
If Bob also measures spin in direction n, he must get a spin-down result. Hence, spin measurements in the same direction are always anti-correlated, although the particles are assumed at this stage to be non-interacting. Einstein, Podolsky and Rosen saw this as evidence of the incompleteness of the Copenhagen interpretation of quantum theory: if there is no particle interaction then the only explanation for this anti-correlation between measurement outcomes is that each particle carries a pre-existing determinate value (appropriately anti-correlated with the value carried by the other particle) for that measurement. Such a property is unaccounted for by the quantum mechanical state description, and their paper concludes:
- While we have thus shown that the wave function does not provide a complete description of the physical reality, we left open the question of whether or not such a description exists. We believe, however, that such a theory is possible.
Although various authors (most notably Niels BohrNiels BohrNiels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
) criticised the ambiguous terminology of the EPR paper, the thought-experiment nevertheless generated a great deal of interest. Their notion of a "complete description" was later formalised by the suggestion of hidden variables that determine the statistics of measurement results, but to which an observer does not have access. Bohmian mechanics provides such a completion of quantum mechanics, in which the hidden variables are explicitly nonlocal, however Bell's Theorem refers to local hidden variables in keeping with Einstein's "Principle of Local Action".
Demonstration
In 1964 John Bell showed that such local hidden variables could never reproduce the statistical outcomes of individual measurements, as predicted by quantum theory. Bell showed that a local hidden variable hypothesis leads to restrictionsBell's theoremIn theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
on the strength of correlations of measurement results. If the Bell inequalities are violated experimentally as predicted by quantum mechanics, then reality cannot be described by such local hidden variables and the mystery of quantum nonlocal causation remains. According to Bell:
- This [grossly nonlocal structure] is characteristic... of any such theory which reproduces exactly the quantum mechanical predictions.
Clauser, Horne, Shimony and Holt (CHSH) reformulated these inequalities in a manner that was more conducive to experimental testing (see CHSH inequalityCHSH inequalityIn physics, the CHSH Bell test is an application of Bell's theorem, intended to distinguish between the entanglement hypothesis of quantum mechanics and local hidden variable theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony and Richard Holt, who described it in a much-cited...
). They proposed a scheme whereby two experimentalists, Alice and Bob, make separate measurements of photon polarizationPhoton polarizationPhoton polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
in two carefully chosen directions, and derived a simple inequality that is obeyed by all local hidden variable theories, but violated by certain measurements on quantum states.
Bell formalized the idea of a hidden variable by introducing the parameter λ to locally characterize measurement results on each system: "It is a matter of indifference... whether λ denotes a single variable or a set... and whether the variables are discrete or continuous". However, it is equivalent (and more intuitive) to think of λ as a local "strategy" that occurs with some probability ρ( ) when an entangled pair of states is created. EPR's criteria of local separability then stipulates that each local strategy defines independent distributions for the outcome probabilities if Alice measures in direction A and Bob measures in direction B:
) when an entangled pair of states is created. EPR's criteria of local separability then stipulates that each local strategy defines independent distributions for the outcome probabilities if Alice measures in direction A and Bob measures in direction B:
where, for instance, denotes the probability of Alice getting the outcome a given λ, and that she measured A.
denotes the probability of Alice getting the outcome a given λ, and that she measured A.
Suppose that λ can take values from some set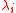 , where 1 ≤ i ≤ k. If each
, where 1 ≤ i ≤ k. If each  has an associated probability ρ(
has an associated probability ρ(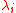 ) of being selected (such that the probabilities sum to unity) we can average over this distribution to obtain a formula for the joint probability of each measurement result:
) of being selected (such that the probabilities sum to unity) we can average over this distribution to obtain a formula for the joint probability of each measurement result:
In the CHSH scheme, the measurement result for the polarization of a photon can take one of two values (informally, whether or not the photon is polarized in that direction). We encode this by allowing a and b to take on values ±1. For each measurement A and B, the correlator E(A, B) is then defined as:
Note that the product ab is equal to 1 if Alice and Bob get the same outcome, and -1 if they get different outcomes. E(A,B) can therefore be seen as the expectationExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
that Alice's and Bob's outcomes are correlated. In the case that Alice chooses from one of two measurements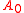 or
or  , and Bob chooses from
, and Bob chooses from 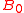 or
or  , the CHSH value for this joint probability distribution is defined as:
, the CHSH value for this joint probability distribution is defined as:
Compare this with the expression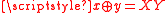 and the discussion in the above example. The CHSH value
and the discussion in the above example. The CHSH value 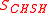 includes a negative contribution of the correlator whenever
includes a negative contribution of the correlator whenever  and
and 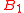 are chosen (
are chosen ( when
when  ), and a positive contribution in all other cases (
), and a positive contribution in all other cases ( ≠
≠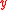 when
when  ). If the joint probability distribution can be described with local strategies as above, it can be shown that the correlation function always obeys the following CHSH inequality:
). If the joint probability distribution can be described with local strategies as above, it can be shown that the correlation function always obeys the following CHSH inequality:
However, if instead of local hidden variables we adopt the rules of quantum theory, it is possible to construct an entangled pair of particles (one each for Alice and Bob) and a set of measurements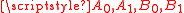 such that
such that 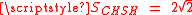 . Experimentalists such as Aspect have verified the quantum violation of the CHSH inequality, as well as other formulations of Bell's inequality, to invalidate the local hidden variables hypothesis and confirm that reality is indeed nonlocal in the EPR sense.
. Experimentalists such as Aspect have verified the quantum violation of the CHSH inequality, as well as other formulations of Bell's inequality, to invalidate the local hidden variables hypothesis and confirm that reality is indeed nonlocal in the EPR sense.
Superquantum nonlocality
Whilst the CHSH inequality gives restrictions on the CHSH value attainable by local hidden variable theories, the rules of quantum theory do not allow us to violate Tsirelson's boundTsirelson's boundTsirelson's bound, also known as Tsirelson's inequality, or in another transliteration, Cirel'son's inequality, is an inequality that imposed an upper limit to quantum mechanical correlations between distant events...
of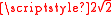 , even if we exploit measurements of entangled particles. The question remained whether this was the maximum CHSH value that can be attained without explicitly allowing instantaneous signaling. In 1994 two physicists, Sandu Popescu and Daniel Rohrlich, formulated an explicit set of non-signalling correlated measurements that give
, even if we exploit measurements of entangled particles. The question remained whether this was the maximum CHSH value that can be attained without explicitly allowing instantaneous signaling. In 1994 two physicists, Sandu Popescu and Daniel Rohrlich, formulated an explicit set of non-signalling correlated measurements that give 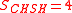 : the algebraic maximum. This demonstrated that there are apparently reasonable theories of parts of Nature that drastically violate the predictions of quantum theory. The attempt to understand what uniquely identifies quantum theory from such general theories motivated an abstraction from physical measurements of nonlocality, to the study of nonlocal boxes.
: the algebraic maximum. This demonstrated that there are apparently reasonable theories of parts of Nature that drastically violate the predictions of quantum theory. The attempt to understand what uniquely identifies quantum theory from such general theories motivated an abstraction from physical measurements of nonlocality, to the study of nonlocal boxes.
Nonlocal boxes generalize the concept of experimentalists making joint measurements from separate locations. As in the discussion above, the choice of measurement is encoded by the input to the box. A two-party nonlocal box takes an input A from Alice and an input B from Bob, and outputs two values a and b for Alice and Bob respectively and separately, where a, b, A and B take values from some finite alphabet (normally ). The box is characterized by the probability of outputting pair a, b, given the inputs A, B. This probability is denoted
). The box is characterized by the probability of outputting pair a, b, given the inputs A, B. This probability is denoted  and obeys the normal probabilisticProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and obeys the normal probabilisticProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
conditions of positivity and normalisation:
and
A box is local, or admits a local hidden variable model, if its output probabilities can be characterized in the following way:
where and
and  describe single input/output probabilities at Alice's or Bob's system alone, and the value of
describe single input/output probabilities at Alice's or Bob's system alone, and the value of  is chosen at random according to some fixed probability distribution given by
is chosen at random according to some fixed probability distribution given by  . Intuitively,
. Intuitively,  corresponds to a hidden variable, or to a shared randomness between Alice and Bob. If a box violates this condition, it is explicitly nonlocal. However, the study of nonlocal boxes often also encapsulates local boxes.
corresponds to a hidden variable, or to a shared randomness between Alice and Bob. If a box violates this condition, it is explicitly nonlocal. However, the study of nonlocal boxes often also encapsulates local boxes.
The set of nonlocal boxes most commonly studied are the so-called non-signalling boxes, for which neither Alice nor Bob can signal their choice of input to the other. Physically, this is a reasonable restriction: setting the input is physically analogous to making a measurement, which should effectively provide a result immediately. Since there may be a large spatial separation between the parties, signalling to Bob would potentially require considerable time to elapse between measurement and result, which is a physically unrealistic scenario.
The non-signalling requirement imposes further conditions on the joint probability, in that the probability of a particular output a or b should depend only on its associated input. This allows for the notion of a reduced or marginal probability on both Alice and Bob's measurements, and is formalised by the conditions:
and
The constraints above are all linear, and so define a polytope representing the set of all non-signalling boxes with a given number of inputs and outputs. Moreover, the polytope is convex because any two boxes that exist in the polytope can be mixed (as above, according to some variable with probabilities
with probabilities  ) to produce another box that also exists within the polytope.
) to produce another box that also exists within the polytope.
Local boxes are clearly non-signalling, however nonlocal boxes may or may not be non-signalling. Since this polytope contains all possible non-signalling boxes of a given number of inputs and outputs, it has as subsets both local boxes and those boxes which can achieve Tsirelson’s bound in accord with quantum mechanical correlations. Indeed, the set of local boxes form a convex sub-polytope of the non-signalling polytope.
Popescu and Rohrlich’s maximum algebraic violation of the CHSH inequality can be reached by a non-signalling box, referred to as a standard PR box after these authors, with joint probability given by:
-
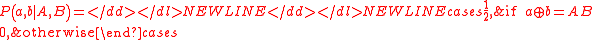
where denotes addition modulo two.
denotes addition modulo two.
Various attempts have been made to explain why Nature does not allow for stronger nonlocality than quantum theory permits. For example, in a recent publication it was found that quantum mechanics cannot be more nonlocal without violating the Heisenberg uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
. Strikingly, it has been discovered that if PR boxes did exist, any distributed computation could be performed with only one bitBitA bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
of communication. An even stronger result is that for any nonlocal box theory which violates Tsirelson's bound, there cannot be a sensible measure of mutual informationMutual informationIn probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between pairs of systems. This suggests a deep link between nonlocality and the information-theoretic properties of quantum mechanics.
Nonlocality vs entanglement
In the media and popular science, quantum nonlocality is often portrayed as being equivalent to entanglement. While it is true that a bipartite quantum state must be entangled in order for it to produce nonlocal correlations, there exist entangled states which do not produce such correlations. A well-known example of this is the Werner stateWerner stateA Werner state is a -dimensional bipartite quantum state that is invariant under all unitary operators of the form U \otimes U. That is, it is a quantum state ρ that satisfies\rho = \rho...
that is entangled for certain values of , but can always be described using local hidden variables. On the other hand, reasonably simple examples of Bell inequalities have been found for which the quantum state giving the largest violation is never a maximally entangled state, showing that entanglement is, in some sense, not even proportional to nonlocality.
, but can always be described using local hidden variables. On the other hand, reasonably simple examples of Bell inequalities have been found for which the quantum state giving the largest violation is never a maximally entangled state, showing that entanglement is, in some sense, not even proportional to nonlocality.
In short, entanglement of a two-party state is necessary but not sufficient for that state to be nonlocal. It is important to recognise that entanglement is more commonly viewed as an algebraic concept, noted for being a precedent to nonlocality as well as quantum teleportationQuantum teleportationQuantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
and superdense codingSuperdense codingSuperdense coding is a technique used in quantum information theory to send two bits of classical information using only one qubit, with the aid of entanglement.- Overview :...
, whereas nonlocality is interpreted according to experimental statistics and is much more involved with the foundations and interpretations of quantum mechanics.
External links
-
-