Puiseux series
Encyclopedia
In mathematics
, Puiseux series are a generalization of formal power series
, first introduced by Isaac Newton
in 1676 and rediscovered by Victor Puiseux
in 1850, that allows for negative and fractional exponents of the indeterminate
. The field of Puiseux series is a (functor
ial) construction which, for any field
(of coefficients) K, gives a field
containing the field of formal Laurent series, and which is algebraically closed
of characteristic
0 when K is so (a statement usually referred to as Puiseux's theorem or sometimes the Newton–Puiseux theorem). The Puiseux expansion is a generalization of the Laurent series expansion
(hence also of the formal series expansion), initially defined for algebraic function
s or (equivalently) branches of algebraic curve
s (a fact also referred to as Puiseux's theorem) and which can be generalized to various settings.
where n and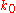
are a nonzero natural num and an integer respectively (which are part of the datum of f): in other words, Puiseux series differ from formal Laurent series in that they allow for fractional exponents of the indeterminate as long as these fractional exponents have bounded denominator (here n), and just as Laurent series, Puiseux series allow for negative exponents of the indeterminate as long as these negative exponents are bounded (here by 
). Addition and multiplication are as expected: one might define them by first “upgrading” the denominator of the exponents to some common denominator and then performing the operation in the corresponding field of formal Laurent series.
In other words, the field of Puiseux series with coefficients in K is the union of the fields
(where n ranges over the nonzero natural numbers), where each element of the union is a field of formal Laurent series over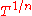 
(considered as an indeterminate), and where each such field is considered as a subfield of the ones with larger n by rewriting the fractional exponents to use a larger denominator (e.g., 
is identified with 
as expected).
This yields a formal definition of the field of Puiseux series: it is the direct limit
of the direct system, indexed over the non-zero natural numbers n ordered by divisibility
, whose objects are all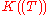
(the field of formal Laurent series, which we rewrite as
for clarity),
with a morphism
being given, whenever m divides n, by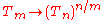
.
(the rationals): the valuation 
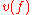of a series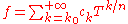
as above is defined to be the smallest rational
such that the coefficient 
of the term with exponent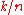 
is non-zero (with the usual convention that the valuation of 0 is +∞). The coefficient 
in question is typically called the valuation coefficient of f.
This valuation in turn defines a (translation-invariant) distance
(which is ultrametric), hence a topology
on the field of Puiseux series by letting the distance from f to 0 be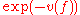
. This justifies a posteriori the notation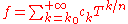
as the series in question does, indeed, converge to f in the Puiseux series field (this is in contrast to Hahn series
which cannot be viewed as converging series).
If the base field K is ordered
, then the field of Puiseux series over K is also naturally (“lexicographically
”) ordered as follows: a non-zero Puiseux series f with 0 is declared positive whenever its valuation coefficient is so. Essentially, this means that any positive rational power of the indeterminate T is made positive, but smaller than any positive element in the base field K.
If the base field K is endowed with a valuation w, then we can construct a different valuation on the field of Puiseux series over K by letting the valuation
of 
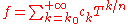be 
where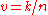
is the previously defined valuation (
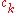is the first non-zero coefficient) and ω is infinitely large (in other words, the value group of 
is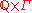 
ordered lexicographically, where Γ is the value group of w). Essentially, this means that the previously defined valuation v is corrected by an infinitesimal amount to take into account the valuation w given on the base field.
) but which was implicit in Newton
's use of the Newton polygon
as early as 1671 and therefore known either as Puiseux's theorem or as the Newton–Puiseux theorem:
Theorem: if K is an algebraically closed field of characteristic zero, then the field of Puiseux series over K is the algebraic closure of the field of formal Laurent series over K.
Very roughly, the proof proceeds essentially by inspecting the Newton polygon of the equation and extracting the coefficients one by one using a valuative form of Newton's method
. Provided algebraic equations can be solved algorithmically in the base field K, then the coefficients of the Puiseux series solutions can be computed to any given order.
For example, the equation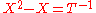
has solutions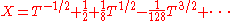
and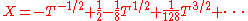
(one readily checks on the first few terms that the sum and product of these two series are 1 and
respectively): this is valid whenever the base field K has characteristic different from 2.
As the powers of 2 in the denominators of the coefficients of the previous example might lead one to believe, the statement of the theorem is not true in positive characteristic. The example of the Artin Schreier equation
shows this: reasoning with valuations shows that X should have valuation 
, and if we rewrite it as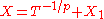 
then
and one shows similarly that
should have valuation 
, and proceeding in that way one obtains the series
since this series makes no sense as a Puiseux series—because the exponents have unbounded denominators— the original equation has no solution. However, such Eisenstein equations
are essentially the only ones not to have a solution, because, if K is algebraically closed of characteristic p>0, then the field of Puiseux series over K is the perfect closure of the maximal tamely ramified
extension of K.
Similarly to the case of algebraic closure, there is an analogous theorem for real closure
: if K is a real closed field, then the field of Puiseux series over K is the real closure of the field of formal Laurent series over K. (This implies the former theorem since any algebraically closed field of characteristic zero is the unique quadratic extension of some real-closed field.)
There is also an analogous result for p-adic closure
: if K is a p-adically closed field with respect to a valuation w, then the field of Puiseux series over K is also p-adically closed.
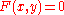over an algebraically closed field K of characteristic zero, and consider a point p on X which we can assume to be (0,0). We also assume that X is not the coordinate axis x=0. Then a Puiseux expansion of (the y coordinate of) X at p is a Puiseux series f having positive valuation such that 
.
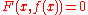More precisely, let us define the branches of X at p to be the points q of the normalization
Y of X which map to p. For each such q, there is a local coordinate t of Y at q (which is a smooth point) such that the coordinates x and y can be expressed as formal power series of t, say
(since K is algebraically closed, we can assume the valuation coefficient to be 1) and 
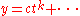: then there is a unique Puiseux series of the form 
(a power series in 
), such that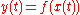 
(the latter expression is meaningful since 
is a well defined power series in t). This is a Puiseux expansion of X at p which is said to be associated to the branch given by q (or simply, the Puiseux expansion of that branch of X), and each Puiseux expansion of X at p is given in this manner for a unique branch of X at p.
This existence of a formal parametrization of the branches of an algebraic curve or function is also referred to as Puiseux's theorem: it has arguably the same mathematical content as the fact that the field of Puiseux series is algebraically closed and is a historically more accurate description of the original author's statement.
For example, the curve
(whose normalization is a line with coordinate t and map 
) has two branches at the double point (0,0), corresponding to the points t = +1 and t = −1 on the normalization, whose Puiseux expansions are 
and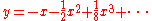 
respectively (here, both are power series because the x coordinate is étale
at the corresponding points in the normalization). At the smooth point (-1,0) (which is t=0 in the normalization), it has a single branch, given by the Puiseux expansion
(the x coordinate ramifies at this point, so it is not a power series).
The curve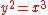
(whose normalization is again a line with coordinate t and map 
), on the other hand, has a single branch at the cusp point
(0,0), whose Puiseux expansion is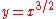
.
, i.e. the field of complex numbers, the Puiseux expansions defined above are convergent
in the sense that for a given choice of n-th root of x, they converge for small enough
, hence define an analytic parametrization of each branch of X in the neighborhood of p (more precisely, the parametrization is by the n-th root of x).
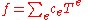, where the support of the coefficients (that is, the set of e such that 
) is the range of an increasing sequence of rational numbers that either is finite or tends to +∞. In other words, such series admit exponents of unbounded denominators, provided there are finitely many terms of exponent less than A for any given bound A. For example, 
is not a Puiseux series, but it is the limit of a Cauchy sequence of Puiseux series (Puiseux polynomials). However, even this completion is still not "maximally complete" in the sense that it admits non-trivial extensions which are valued fields having the same value group and residue field, hence the opportunity of completing it even more:
Hahn series
are a further (larger) generalization of Puiseux series, introduced by Hans Hahn
(in the course of the proof of his embedding theorem
in 1907 and then studied by him in his approach to Hilbert's seventeenth problem
), where instead of requiring the exponents to have bounded denominator they are required to form a well-ordered subset
of the value group (usually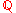
or 
). These were later further generalized by Anatoly Maltsev
and Bernhard Neumann
to a non-commutative setting (they are therefore sometimes known as Hahn-Mal'cev-Neumann series). Using Hahn series, it is possible to give a description of the algebraic closure of the field of power series in positive characteristic which is somewhat analogous to the field of Puiseux series.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Puiseux series are a generalization of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
, first introduced by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
in 1676 and rediscovered by Victor Puiseux
Victor Puiseux
Victor Alexandre Puiseux was a French mathematician and astronomer. Puiseux series are named after him, as is in part the Bertrand–Diquet–Puiseux theorem.-Life:...
in 1850, that allows for negative and fractional exponents of the indeterminate
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
. The field of Puiseux series is a (functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ial) construction which, for any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(of coefficients) K, gives a field
containing the field of formal Laurent series, and which is algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0 when K is so (a statement usually referred to as Puiseux's theorem or sometimes the Newton–Puiseux theorem). The Puiseux expansion is a generalization of the Laurent series expansion
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
(hence also of the formal series expansion), initially defined for algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s or (equivalently) branches of algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s (a fact also referred to as Puiseux's theorem) and which can be generalized to various settings.
Field of Puiseux series
If K is a field then we can define the field of Puiseux series with coefficients in K (or over K) informally as the set of formal expressions of the formwhere n and
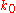are a nonzero natural num and an integer respectively (which are part of the datum of f): in other words, Puiseux series differ from formal Laurent series in that they allow for fractional exponents of the indeterminate as long as these fractional exponents have bounded denominator (here n), and just as Laurent series, Puiseux series allow for negative exponents of the indeterminate as long as these negative exponents are bounded (here by ). Addition and multiplication are as expected: one might define them by first “upgrading” the denominator of the exponents to some common denominator and then performing the operation in the corresponding field of formal Laurent series.In other words, the field of Puiseux series with coefficients in K is the union of the fields
(where n ranges over the nonzero natural numbers), where each element of the union is a field of formal Laurent series over 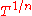(considered as an indeterminate), and where each such field is considered as a subfield of the ones with larger n by rewriting the fractional exponents to use a larger denominator (e.g., is identified with as expected).This yields a formal definition of the field of Puiseux series: it is the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of the direct system, indexed over the non-zero natural numbers n ordered by divisibility
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
, whose objects are all
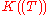(the field of formal Laurent series, which we rewrite as for clarity),with a morphism
being given, whenever m divides n, by
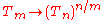.Valuation and order
The Puiseux series over a field K form a valued field with value group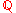 (the rationals): the valuation 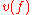of a series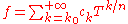as above is defined to be the smallest rational
such that the coefficient of the term with exponent 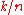is non-zero (with the usual convention that the valuation of 0 is +∞). The coefficient in question is typically called the valuation coefficient of f.This valuation in turn defines a (translation-invariant) distance
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
(which is ultrametric), hence a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
on the field of Puiseux series by letting the distance from f to 0 be
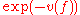. This justifies a posteriori the notation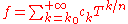as the series in question does, indeed, converge to f in the Puiseux series field (this is in contrast to Hahn series
Hahn series
In mathematics, Hahn series are a type of formal infinite series. They are a generalization of Puiseux series and were first introduced by Hans Hahn in 1907...
which cannot be viewed as converging series).
If the base field K is ordered
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
, then the field of Puiseux series over K is also naturally (“lexicographically
Lexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
”) ordered as follows: a non-zero Puiseux series f with 0 is declared positive whenever its valuation coefficient is so. Essentially, this means that any positive rational power of the indeterminate T is made positive, but smaller than any positive element in the base field K.
If the base field K is endowed with a valuation w, then we can construct a different valuation on the field of Puiseux series over K by letting the valuation
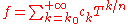of be where
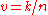is the previously defined valuation ( 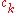is the first non-zero coefficient) and ω is infinitely large (in other words, the value group of is 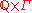ordered lexicographically, where Γ is the value group of w). Essentially, this means that the previously defined valuation v is corrected by an infinitesimal amount to take into account the valuation w given on the base field.Algebraic closedness of Puiseux series
One essential property of Puiseux series is expressed by the following theorem, attributed to Puiseux (for) but which was implicit in NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's use of the Newton polygon
Newton polygon
In mathematics, the Newton polygon is a tool for understanding the behaviour of polynomials over local fields.In the original case, the local field of interest was the field of formal Laurent series in the indeterminate X, i.e. the field of fractions of the formal power series ringover K, where K...
as early as 1671 and therefore known either as Puiseux's theorem or as the Newton–Puiseux theorem:
Theorem: if K is an algebraically closed field of characteristic zero, then the field of Puiseux series over K is the algebraic closure of the field of formal Laurent series over K.
Very roughly, the proof proceeds essentially by inspecting the Newton polygon of the equation and extracting the coefficients one by one using a valuative form of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. Provided algebraic equations can be solved algorithmically in the base field K, then the coefficients of the Puiseux series solutions can be computed to any given order.
For example, the equation
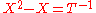has solutions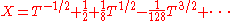and
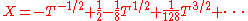
(one readily checks on the first few terms that the sum and product of these two series are 1 and
respectively): this is valid whenever the base field K has characteristic different from 2.As the powers of 2 in the denominators of the coefficients of the previous example might lead one to believe, the statement of the theorem is not true in positive characteristic. The example of the Artin Schreier equation
shows this: reasoning with valuations shows that X should have valuation , and if we rewrite it as 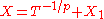thenand one shows similarly that
should have valuation , and proceeding in that way one obtains the seriessince this series makes no sense as a Puiseux series—because the exponents have unbounded denominators— the original equation has no solution. However, such Eisenstein equations
Eisenstein's criterion
In mathematics, Eisenstein's criterion gives an easily checked sufficient condition for a polynomial with integer coefficients to be irreducible over the rational numbers...
are essentially the only ones not to have a solution, because, if K is algebraically closed of characteristic p>0, then the field of Puiseux series over K is the perfect closure of the maximal tamely ramified
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
extension of K.
Similarly to the case of algebraic closure, there is an analogous theorem for real closure
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
: if K is a real closed field, then the field of Puiseux series over K is the real closure of the field of formal Laurent series over K. (This implies the former theorem since any algebraically closed field of characteristic zero is the unique quadratic extension of some real-closed field.)
There is also an analogous result for p-adic closure
P-adically closed field
In mathematics, a p-adically closed field is a field that enjoys a closure property that is a close analogue for p-adic fields to what real closure is to the real field. They were introduced by James Ax and Simon B. Kochen in 1965.- Definition :...
: if K is a p-adically closed field with respect to a valuation w, then the field of Puiseux series over K is also p-adically closed.
Algebraic curves
Let X be an algebraic curve given by an affine equation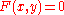 over an algebraically closed field K of characteristic zero, and consider a point p on X which we can assume to be (0,0). We also assume that X is not the coordinate axis x=0. Then a Puiseux expansion of (the y coordinate of) X at p is a Puiseux series f having positive valuation such that 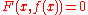.More precisely, let us define the branches of X at p to be the points q of the normalization
Noether normalization lemma
In mathematics, the Noether normalization lemma is a result of commutative algebra, introduced in . A simple version states that for any field k, and any finitely generated commutative k-algebra A, there exists a nonnegative integer d and algebraically independent elements y1, y2, ..., yd in Asuch...
Y of X which map to p. For each such q, there is a local coordinate t of Y at q (which is a smooth point) such that the coordinates x and y can be expressed as formal power series of t, say
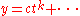(since K is algebraically closed, we can assume the valuation coefficient to be 1) and : then there is a unique Puiseux series of the form (a power series in ), such that 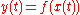(the latter expression is meaningful since is a well defined power series in t). This is a Puiseux expansion of X at p which is said to be associated to the branch given by q (or simply, the Puiseux expansion of that branch of X), and each Puiseux expansion of X at p is given in this manner for a unique branch of X at p.This existence of a formal parametrization of the branches of an algebraic curve or function is also referred to as Puiseux's theorem: it has arguably the same mathematical content as the fact that the field of Puiseux series is algebraically closed and is a historically more accurate description of the original author's statement.
For example, the curve
(whose normalization is a line with coordinate t and map ) has two branches at the double point (0,0), corresponding to the points t = +1 and t = −1 on the normalization, whose Puiseux expansions are and 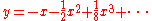respectively (here, both are power series because the x coordinate is étaleÉtale morphism
In algebraic geometry, a field of mathematics, an étale morphism is an algebraic analogue of the notion of a local isomorphism in the complex analytic topology. They satisfy the hypotheses of the implicit function theorem, but because open sets in the Zariski topology are so large, they are not...
at the corresponding points in the normalization). At the smooth point (-1,0) (which is t=0 in the normalization), it has a single branch, given by the Puiseux expansion
(the x coordinate ramifies at this point, so it is not a power series).The curve
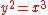(whose normalization is again a line with coordinate t and map ), on the other hand, has a single branch at the cusp pointCusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
(0,0), whose Puiseux expansion is
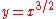.Analytic convergence
When, i.e. the field of complex numbers, the Puiseux expansions defined above are convergentRadius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
in the sense that for a given choice of n-th root of x, they converge for small enough
, hence define an analytic parametrization of each branch of X in the neighborhood of p (more precisely, the parametrization is by the n-th root of x).Generalization
The field of Puiseux series is not complete, but its completion can be easily described: it is the field of formal expressions of the form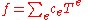, where the support of the coefficients (that is, the set of e such that ) is the range of an increasing sequence of rational numbers that either is finite or tends to +∞. In other words, such series admit exponents of unbounded denominators, provided there are finitely many terms of exponent less than A for any given bound A. For example, is not a Puiseux series, but it is the limit of a Cauchy sequence of Puiseux series (Puiseux polynomials). However, even this completion is still not "maximally complete" in the sense that it admits non-trivial extensions which are valued fields having the same value group and residue field, hence the opportunity of completing it even more:Hahn series
Hahn series
In mathematics, Hahn series are a type of formal infinite series. They are a generalization of Puiseux series and were first introduced by Hans Hahn in 1907...
are a further (larger) generalization of Puiseux series, introduced by Hans Hahn
Hans Hahn
Hans Hahn was an Austrian mathematician who made contributions to functional analysis, topology, set theory, the calculus of variations, real analysis, and order theory.-Biography:...
(in the course of the proof of his embedding theorem
Hahn embedding theorem
In mathematics, especially in the area of abstract algebra dealing with ordered structures on abelian groups, the Hahn embedding theorem gives a simple description of all linearly ordered abelian groups....
in 1907 and then studied by him in his approach to Hilbert's seventeenth problem
Hilbert's seventeenth problem
Hilbert's seventeenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It entails expression of definite rational functions as quotients of sums of squares...
), where instead of requiring the exponents to have bounded denominator they are required to form a well-ordered subset
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
of the value group (usually
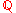or ). These were later further generalized by Anatoly MaltsevAnatoly Maltsev
Anatoly Ivanovich Maltsev was born in Misheronsky, near Moscow, and died in Novosibirsk, USSR. He was a mathematician noted for his work on the decidability of various algebraic groups...
and Bernhard Neumann
Bernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
to a non-commutative setting (they are therefore sometimes known as Hahn-Mal'cev-Neumann series). Using Hahn series, it is possible to give a description of the algebraic closure of the field of power series in positive characteristic which is somewhat analogous to the field of Puiseux series.