Pseudosphere
Encyclopedia
In geometry
, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature
. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid.
−1/R2 (precisely, a complete, simply connected surface of that curvature), by analogy with the sphere of radius R, which is a surface of curvature 1/R2. The term was introduced by Eugenio Beltrami
in his 1868 paper on models of hyperbolic geometry
.
The term is also used to refer to a certain surface called the tractricoid: the result of revolving
a tractrix
about its asymptote
. As an example, the (half) pseudosphere (with radius 1) is the surface of revolution of the tractrix parametrized by
It is a singular space
(the equator is a singularity), but away from the singularities, it has constant negative Gaussian curvature
and therefore is locally isometric
to a hyperbolic plane
.
The name "pseudosphere" comes about because it is a two-dimensional
surface
of constant negative curvature just like a sphere with positive Gauss curvature.
Just as the sphere
has at every point a positively curved geometry of a dome
the whole pseudosphere has at every point the negatively curved geometry of a saddle
.
As early as 1639 Christiaan Huygens found that the volume and the surface area of the pseudosphere are finite, despite the infinite extent of the shape along the axis of rotation. For a given edge radius
R, the area
is 4πR2 just as it is for the sphere, while the volume
is 2/3 πR3 and therefore half that of a sphere of that radius.
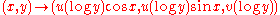
where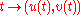
is the arclength parametrization of the tractrix.
of the hyperbolic plane, the hyperboloid is referred to as a pseudosphere.
This usage of the word is because the hyperboloid can be thought of as a sphere of imaginary radius, embedded in a Minkowski space
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid.
Theoretical Pseudosphere
In its general interpretation, a pseudosphere of radius R is any surface of curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
−1/R2 (precisely, a complete, simply connected surface of that curvature), by analogy with the sphere of radius R, which is a surface of curvature 1/R2. The term was introduced by Eugenio Beltrami
Eugenio Beltrami
Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...
in his 1868 paper on models of hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
.
Tractricoid
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
a tractrix
Tractrix
Tractrix is the curve along which a small object moves, under the influence of friction, when pulled on a horizontal plane by a piece of thread and a puller that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of...
about its asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
. As an example, the (half) pseudosphere (with radius 1) is the surface of revolution of the tractrix parametrized by
It is a singular space
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
(the equator is a singularity), but away from the singularities, it has constant negative Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
and therefore is locally isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to a hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
.
The name "pseudosphere" comes about because it is a two-dimensional
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
of constant negative curvature just like a sphere with positive Gauss curvature.
Just as the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
has at every point a positively curved geometry of a dome
Dome
A dome is a structural element of architecture that resembles the hollow upper half of a sphere. Dome structures made of various materials have a long architectural lineage extending into prehistory....
the whole pseudosphere has at every point the negatively curved geometry of a saddle
Saddle surface
A saddle surface is a smooth surface containing one or more saddle points.The term derives from the peculiar shape of historical horse saddles, which curve both up and down....
.
As early as 1639 Christiaan Huygens found that the volume and the surface area of the pseudosphere are finite, despite the infinite extent of the shape along the axis of rotation. For a given edge radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
R, the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
is 4πR2 just as it is for the sphere, while the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
is 2/3 πR3 and therefore half that of a sphere of that radius.
Universal covering space
The half pseudosphere of curvature −1 is covered by the portion of the hyperbolic upper half-plane with abscissa y ≥ 1. The covering map is periodic in the x direction of period 2π, and takes the horocycles y = c to the meridians of the pseudosphere and the vertical geodesics x = c to the tractrices that generate the pseudosphere. This mapping is a local isometry, and thus exhibits the portion y ≥ 1 of the upper half-plane as the universal covering space of the pseudosphere. The precise mapping is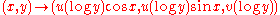where
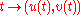is the arclength parametrization of the tractrix.Hyperboloid
In some sources that use the Hyperboloid modelHyperboloid model
In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
of the hyperbolic plane, the hyperboloid is referred to as a pseudosphere.
This usage of the word is because the hyperboloid can be thought of as a sphere of imaginary radius, embedded in a Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
.
See also
- Dini's surfaceDini's surfaceIn geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere. It is named after Ulisse Dini and described by the following parametric equations:- Uses :...
- Hyperboloid structureHyperboloid structureHyperboloid structures are architectural structures designed with hyperboloid geometry. Often these are tall structures such as towers where the hyperboloid geometry's structural strength is used to support an object high off the ground, but hyperboloid geometry is also often used for decorative...
- Sine–Gordon equation
- SphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
- Surface of revolutionSurface of revolutionA surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
External links
- Non Euclid
- Crocheting the Hyperbolic Plane: An Interview with David Henderson and Daina Taimina
- Prof. C.T.J. Dodson's web site at University of Manchester
- Interactive demonstration of the pseudosphere (at the University of ManchesterUniversity of ManchesterThe University of Manchester is a public research university located in Manchester, United Kingdom. It is a "red brick" university and a member of the Russell Group of research-intensive British universities and the N8 Group...
)