Probabilistic method
Encyclopedia
The probabilistic method is a nonconstructive method, primarily used in combinatorics
and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability
that the result is of the prescribed kind is more than zero. Although the proof uses probability, the final conclusion is determined for certain, without any possible error.
This method has now been applied to other areas of mathematics
such as number theory
, linear algebra
, and real analysis
,
as well as in computer science
(e.g. randomized rounding
).
Similarly, showing that the probability is (strictly) less than 1 can be used to prove the existence of an object that does not satisfy the prescribed properties.
Another way to use the probabilistic method is by calculating the expected value
of some random variable
. If it can be shown that the random variable can take on a value less than the expected value, this proves that the random variable can also take on some value greater than the expected value.
Common tools used in the probabilistic method include Markov's inequality
, the Chernoff bound
, and the Lovász local lemma
.
containing a large number of Hamiltonian cycles), many of the most well known proofs using this method are due to Erdős. The first example below describes one such result from 1947 that gives a proof of a lower bound for the Ramsey number
R(r, r).
on n vertices. We wish to show (for small enough values of n) that it is possible to color the edges of the graph in two colors (say red and blue) so that there is no complete subgraph on r vertices which is monochromatic (every edge colored the same color).
To do so, we color the graph randomly. Color each edge independently with probability 1/2 of being red and 1/2 of being blue. We calculate the expected number of monochromatic subgraphs on r vertices as follows:
For any set S of r vertices from our graph, define the variable X(S) to be 1 if every edge amongst the r vertices is the same color, and 0 otherwise. Note that the number of monochromatic r-subgraphs is the sum of X(S) over all possible subsets. For any S, the expected value
of X(S) is simply the probability that all of the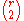
edges in S are the same color,
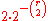
(the factor of 2 comes because there are two possible colors).
This holds true for any of the C(n,r) possible subsets we could have chosen, so we have that the sum of E[X(S)] over all S is
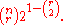
The sum of an expectation is the expectation of the sum (regardless of whether the variables are independent
), so the expectation of the sum (the expected number of monochromatic r-subgraphs) is
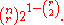
Consider what happens if this value is less than 1. The number of monochromatic r-subgraphs in our random coloring will always be an integer, so at least one coloring must have less than the expected value. But the only integer which satisfies this criterion is 0. Thus if
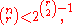
some coloring fits our desired criterion, so by definition R(r, r) must be bigger than n. In particular, R(r, r) must grow at least exponentially
with r.
A peculiarity of this argument is that it is entirely nonconstructive. Even though it proves (for example) that almost every coloring of the complete graph on (1.1)r vertices contains no monochromatic r-subgraph, it gives no explicit example of such a coloring. The problem of finding such a coloring has been open for more than 50 years.
: given positive integers g and k, does there exist a graph G containing only cycles
of length at least g, such that the chromatic number of G is at least k?
It can be shown that such a graph exists for any g and k, and the proof is reasonably simple. Let n be very large and consider a random graph G on n vertices, where every edge in G exists with probability p=n1/g-1. It can be shown that with positive probability, the following two properties hold:
Proof. Let X be the number cycles of length less than g. Number of cycles of length i in the complete graph on n vertices is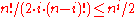
and each of them is present in G with probability 
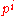. Hence by Markov's inequality we have
.
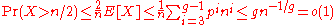Proof. Let Y be the size of the largest independent set in G. Clearly, we have
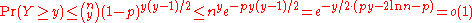
when
.
Here comes the trick: since G has these two properties, we can remove at most n/2 vertices from G to obtain a new graph G on n' vertices that contains only cycles of length at least g. We can see that this new graph has no independent set of size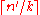 
. Hence G' has chromatic number at least k, as chromatic number is lower bounded by 'number of vertices/size of largest independent set'.
This result gives a hint as to why the computation of the chromatic number
of a graph is so difficult: even when there are no local reasons (such as small cycles) for a graph to require many colors the chromatic number can still be arbitrarily large.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the result is of the prescribed kind is more than zero. Although the proof uses probability, the final conclusion is determined for certain, without any possible error.
This method has now been applied to other areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
such as number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, and real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
,
as well as in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
(e.g. randomized rounding
Randomized rounding
Within computer science and operations research,many combinatorial optimization problems are computationally intractable to solve exactly ....
).
Introduction
If every object in a collection of objects fails to have a certain property, then the probability that a random object chosen from the collection has that property is zero. Turning this around, if the probability that the random object has the property is greater than zero, then this proves the existence of at least one object in the collection that has the property. It doesn't matter if the probability is vanishingly small; any positive probability will do.Similarly, showing that the probability is (strictly) less than 1 can be used to prove the existence of an object that does not satisfy the prescribed properties.
Another way to use the probabilistic method is by calculating the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of some random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
. If it can be shown that the random variable can take on a value less than the expected value, this proves that the random variable can also take on some value greater than the expected value.
Common tools used in the probabilistic method include Markov's inequality
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
, the Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
, and the Lovász local lemma
Lovász local lemma
In probability theory, if a large number of events are all independent of one another and each has probability less than 1, then there is a positive probability that none of the events will occur...
.
Two examples due to Erdős
Although others before him proved theorems via the probabilistic method (for example, Szele's 1943 result that there exist tournamentsTournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
containing a large number of Hamiltonian cycles), many of the most well known proofs using this method are due to Erdős. The first example below describes one such result from 1947 that gives a proof of a lower bound for the Ramsey number
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
R(r, r).
First example
Suppose we have a complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on n vertices. We wish to show (for small enough values of n) that it is possible to color the edges of the graph in two colors (say red and blue) so that there is no complete subgraph on r vertices which is monochromatic (every edge colored the same color).
To do so, we color the graph randomly. Color each edge independently with probability 1/2 of being red and 1/2 of being blue. We calculate the expected number of monochromatic subgraphs on r vertices as follows:
For any set S of r vertices from our graph, define the variable X(S) to be 1 if every edge amongst the r vertices is the same color, and 0 otherwise. Note that the number of monochromatic r-subgraphs is the sum of X(S) over all possible subsets. For any S, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of X(S) is simply the probability that all of the
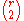edges in S are the same color,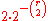(the factor of 2 comes because there are two possible colors).
This holds true for any of the C(n,r) possible subsets we could have chosen, so we have that the sum of E[X(S)] over all S is
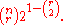
The sum of an expectation is the expectation of the sum (regardless of whether the variables are independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
), so the expectation of the sum (the expected number of monochromatic r-subgraphs) is
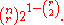
Consider what happens if this value is less than 1. The number of monochromatic r-subgraphs in our random coloring will always be an integer, so at least one coloring must have less than the expected value. But the only integer which satisfies this criterion is 0. Thus if
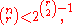
some coloring fits our desired criterion, so by definition R(r, r) must be bigger than n. In particular, R(r, r) must grow at least exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
with r.
A peculiarity of this argument is that it is entirely nonconstructive. Even though it proves (for example) that almost every coloring of the complete graph on (1.1)r vertices contains no monochromatic r-subgraph, it gives no explicit example of such a coloring. The problem of finding such a coloring has been open for more than 50 years.
Second example
A 1959 paper of Erdős (see reference cited below) addressed the following problem in graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
: given positive integers g and k, does there exist a graph G containing only cycles
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
of length at least g, such that the chromatic number of G is at least k?
It can be shown that such a graph exists for any g and k, and the proof is reasonably simple. Let n be very large and consider a random graph G on n vertices, where every edge in G exists with probability p=n1/g-1. It can be shown that with positive probability, the following two properties hold:
- G contains at most n/2 cycles of length less than g.
Proof. Let X be the number cycles of length less than g. Number of cycles of length i in the complete graph on n vertices is
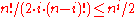and each of them is present in G with probability 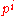. Hence by Markov's inequality we have 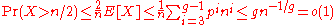.- G contains no independent setIndependent set (graph theory)In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
of size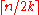
.
Proof. Let Y be the size of the largest independent set in G. Clearly, we have
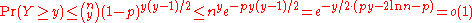
when
.Here comes the trick: since G has these two properties, we can remove at most n/2 vertices from G to obtain a new graph G on n
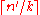. Hence GThis result gives a hint as to why the computation of the chromatic number
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
of a graph is so difficult: even when there are no local reasons (such as small cycles) for a graph to require many colors the chromatic number can still be arbitrarily large.
See also
- Random graphRandom graphIn mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
- Probabilistic proofs of non-probabilistic theoremsProbabilistic proofs of non-probabilistic theoremsProbability theory routinely uses results from other fields of mathematics . The opposite cases, collected below, are relatively rare; however, probability theory is used systematically in combinatorics via the probabilistic method. They are particularly used for non-constructive proofs.-Analysis:*...
- Method of conditional probabilitiesMethod of conditional probabilitiesIn mathematics and computer science, the probabilistic method is used to prove the existence of mathematical objects with desired combinatorial properties. The proofs are probabilistic — they work by showing that a random object, chosen from some probability distribution, has the desired properties...
- Interactive proof systemInteractive proof systemIn computational complexity theory, an interactive proof system is an abstract machine that models computation as the exchange of messages between two parties. The parties, the verifier and the prover, interact by exchanging messages in order to ascertain whether a given string belongs to a...