Petrov classification
Encyclopedia
In differential geometry and theoretical physics
, the Petrov classification describes the possible algebraic symmetries
of the Weyl tensor
at each event in a Lorentzian manifold.
It is most often applied in studying exact solutions of Einstein's field equations, but strictly speaking the classification is a theorem in pure mathematics applying to any Lorentzian manifold, independent of any physical interpretation. The classification was found in 1954 by A. Z. Petrov.
such as the Weyl tensor
, evaluated at some event, as acting on the space of bivector
s at that event like a linear operator acting on a vector space:
Then, it is natural to consider the problem of finding eigenvalues
and eigenvectors (which are now referred to as eigenbivectors) 
such that
In (four dimensional) Lorentzian spacetimes, there is a six dimensional space of antisymmetric bivectors at each event. However, the symmetries of the Weyl tensor imply that any eigenbivectors must belong to a four dimensional subset.
Thus, the Weyl tensor (at a given event) can in fact have at most four linearly independent eigenbivectors.
Just as in the theory of the eigenvectors of an ordinary linear operator, the eigenbivectors of the Weyl tensor can occur with various multiplicities. Just as in the case of ordinary linear operators, any multiplicities among the eigenbivectors indicates a kind of algebraic symmetry of the Weyl tensor at the given event. Just as you would expect from the theory of the eigenvalues of an ordinary linear operator on a four dimensional vector space, the different types of Weyl tensor (at a given event) can be determined by solving a certain quartic polynomial.
These eigenbivectors are associated with certain null vectors in the original spacetime, which are called the principal null directions (at a given event).
The relevant multilinear algebra
is somewhat involved (see the citations below), but the resulting classification theorem states that there are precisely six possible types of algebraic symmetry. These are known as the Petrov types:
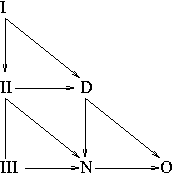
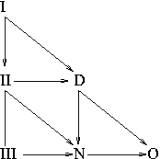
A Weyl tensor which has type I (at some event) is called algebraically general; otherwise, it is called algebraically special (at that event). Different events in a given spacetime can have different Petrov types. The possible transitions between Petrov types are shown in the figure, which can also be interpreted as stating that some of the Petrov types are "more special" than others. For example, type I, the most general type, can degenerate to types II or D, while type II can degenerate to types III, N, or D.
on a Lorentzian manifold
, the Weyl tensor 
for this metric may be computed. If the Weyl tensor is algebraically special at some 
, there is a useful set of conditions, found by Lluis (or Louis) Bel and Robert Debever, for determining precisely the Petrov type at 
. Denoting the Weyl tensor components at 
by 
(assumed non-zero, i.e., not of type O), the Bel criteria may be stated as:
where
is necessarily null and unique (up to scaling).
where
is necessarily null and unique (up to scaling).
and 
(
)
where
is necessarily null and unique (up to scaling).
, 
(
)
and
, 
(
).
where
is the dual of the Weyl tensor at 
.
In fact, for each criterion above, there are equivalent conditions for the Weyl tensor to have that type. These equivalent conditions are stated in terms of the dual and self-dual of the Weyl tensor and certain bivectors and are collected together in Hall (2004).
The Bel criteria find application in general relativity where determining the Petrov type of algebraically special Weyl tensors is accomplished by searching for null vectors.
, the various algebraically special Petrov types have some interesting physical interpretations, the classification then sometimes being called the classification of gravitational fields.
Type D regions are associated with the gravitational fields of isolated massive objects, such as stars. More precisely, type D fields occur as the field of a gravitating object which is completely characterized by its mass and angular momentum. (A more general object might have nonzero higher multipole moments
.) The two double principal null directions define "radially" ingoing and outgoing null congruences near the object which is the source of the field.
The electrogravitic tensor
(or tidal tensor) in a type D region is very closely analogous to the gravitational fields which are described in Newtonian gravity by a Coulomb type gravitational potential. Such a tidal field is characterized by tension in one direction and compression in the orthogonal directions; the eigenvalues have the pattern (-2,1,1). For example, a spacecraft orbiting the Earth experiences a tiny tension along a radius from the center of the Earth, and a tiny compression in the orthogonal directions. Just as in Newtonian gravitation, this tidal field typically decays like
, where 
is the distance from the object.
If the object is rotating about some axis, in addition to the tidal effects, there will be various gravitomagnetic
effects, such as spin-spin forces on gyroscopes carried by an observer. In the Kerr vacuum
, which is the best known example of type D vacuum solution, this part of the field decays like
.
Type III regions are associated with a kind of longitudinal
gravitational radiation. In such regions, the tidal forces have a shearing effect. This possibility is often neglected, in part because the gravitational radiation which arises in weak-field theory is type N, and in part because type III radiation decays like
, which is faster than type N radiation.
Type N regions are associated with transverse
gravitational radiation, which is the type astronomers are trying to detect with LIGO
.
The quadruple principal null direction corresponds to the wave vector
describing the direction of propagation of this radiation. It typically decays like
, so the long-range radiation field is type N.
Type II regions combine the effects noted above for types D, III, and N, in a rather complicated nonlinear way.
Type O regions, or conformally flat
regions, are associated with places where the Weyl tensor vanishes identically. In this case, the curvature is said to be pure Ricci. In a conformally flat region, any gravitational effects must be due to the immediate presence of matter or the field
energy
of some nongravitational field (such as an electromagnetic field
). In a sense, this means that any distant objects are not exerting any long range influence on events in our region. More precisely, if there are any time varying gravitational fields in distant regions, the news has not yet reached our conformally flat region.
Gravitational radiation emitted from an isolated system will usually not be algebraically special.
The peeling theorem describes the way in which, as one moves farther way from the source of the radiation, the various components of the radiation field "peel" off, until finally only type N radiation is noticeable at large distances. This is similar to the electromagnetic peeling theorem.
More generally, any spherically symmetric spacetime
must be of type D (or O). All algebraically special spacetimes having various types of stress-energy tensor
are known, for example, all the type D vacuum solutions.
Some classes of solutions can be invariantly characterized using algebraic symmetries of the Weyl tensor: for example, the class of non-conformally flat null electrovacuum
or null dust
solutions admitting an expanding but nontwisting null congruence is precisely the class of Robinson/Trautmann spacetimes. These are usually type II, but include type III and type N examples.
. Their approach uses a null frame basis approach, that is a frame basis containing two null vectors 
and 
, along with 
spacelike vectors. Frame basis components of the Weyl tensor
are classified by their transformation properties under local Lorentz boosts. If particular Weyl components vanish, then
and/or 
are said to be Weyl-Aligned Null Directions (WANDs). In four dimensions, 
is a WAND if and only if it is a principal null direction in the sense defined above. This approach gives a natural higher-dimensional extension of each of the various algebraic types II,D etc. defined above.
An alternative, but inequivalent, generalization was previously defined by de Smet (2002), based on a spinorial approach. However, the de Smet is restricted to 5 dimensions only.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Petrov classification describes the possible algebraic symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
at each event in a Lorentzian manifold.
It is most often applied in studying exact solutions of Einstein's field equations, but strictly speaking the classification is a theorem in pure mathematics applying to any Lorentzian manifold, independent of any physical interpretation. The classification was found in 1954 by A. Z. Petrov.
The classification theorem
We can think of a fourth rank tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
such as the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
, evaluated at some event, as acting on the space of bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s at that event like a linear operator acting on a vector space:
Then, it is natural to consider the problem of finding eigenvalues
and eigenvectors (which are now referred to as eigenbivectors) such thatIn (four dimensional) Lorentzian spacetimes, there is a six dimensional space of antisymmetric bivectors at each event. However, the symmetries of the Weyl tensor imply that any eigenbivectors must belong to a four dimensional subset.
Thus, the Weyl tensor (at a given event) can in fact have at most four linearly independent eigenbivectors.
Just as in the theory of the eigenvectors of an ordinary linear operator, the eigenbivectors of the Weyl tensor can occur with various multiplicities. Just as in the case of ordinary linear operators, any multiplicities among the eigenbivectors indicates a kind of algebraic symmetry of the Weyl tensor at the given event. Just as you would expect from the theory of the eigenvalues of an ordinary linear operator on a four dimensional vector space, the different types of Weyl tensor (at a given event) can be determined by solving a certain quartic polynomial.
These eigenbivectors are associated with certain null vectors in the original spacetime, which are called the principal null directions (at a given event).
The relevant multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
is somewhat involved (see the citations below), but the resulting classification theorem states that there are precisely six possible types of algebraic symmetry. These are known as the Petrov types:
- Type I : four simple principal null directions,
- Type II : one double and two simple principal null directions,
- Type D : two double principal null directions,
- Type III: one triple and one simple principal null direction,
- Type N : one quadruple principal null direction,
- Type O : the Weyl tensor vanishes.
A Weyl tensor which has type I (at some event) is called algebraically general; otherwise, it is called algebraically special (at that event). Different events in a given spacetime can have different Petrov types. The possible transitions between Petrov types are shown in the figure, which can also be interpreted as stating that some of the Petrov types are "more special" than others. For example, type I, the most general type, can degenerate to types II or D, while type II can degenerate to types III, N, or D.
Bel criteria
Given a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on a Lorentzian manifold
, the Weyl tensor for this metric may be computed. If the Weyl tensor is algebraically special at some , there is a useful set of conditions, found by Lluis (or Louis) Bel and Robert Debever, for determining precisely the Petrov type at . Denoting the Weyl tensor components at by (assumed non-zero, i.e., not of type O), the Bel criteria may be stated as:-
is type N if and only if there exists a vector 
satisfying
where
is necessarily null and unique (up to scaling).- If
is not type N, then 
is of type III if and only if there exists a vector 
satisfying
where
is necessarily null and unique (up to scaling).-
is of type II if and only if there exists a vector 
satisfying
and ()where
is necessarily null and unique (up to scaling).-
is of type D if and only if there exists two linearly independent vectors 
, 
satisfying the conditions
, ()and
, ().where
is the dual of the Weyl tensor at .In fact, for each criterion above, there are equivalent conditions for the Weyl tensor to have that type. These equivalent conditions are stated in terms of the dual and self-dual of the Weyl tensor and certain bivectors and are collected together in Hall (2004).
The Bel criteria find application in general relativity where determining the Petrov type of algebraically special Weyl tensors is accomplished by searching for null vectors.
Physical Interpretation
According to general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the various algebraically special Petrov types have some interesting physical interpretations, the classification then sometimes being called the classification of gravitational fields.
Type D regions are associated with the gravitational fields of isolated massive objects, such as stars. More precisely, type D fields occur as the field of a gravitating object which is completely characterized by its mass and angular momentum. (A more general object might have nonzero higher multipole moments
Multipole moments
In mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
.) The two double principal null directions define "radially" ingoing and outgoing null congruences near the object which is the source of the field.
The electrogravitic tensor
Electrogravitic tensor
In general relativity, the tidal tensor or gravitoelectric tensor is one of the pieces in the Bel decomposition of the Riemann tensor. It is physically interpreted as giving the tidal stresses on small bits of a material object , or the tidal accelerations of a small cloud of test particles in a...
(or tidal tensor) in a type D region is very closely analogous to the gravitational fields which are described in Newtonian gravity by a Coulomb type gravitational potential. Such a tidal field is characterized by tension in one direction and compression in the orthogonal directions; the eigenvalues have the pattern (-2,1,1). For example, a spacecraft orbiting the Earth experiences a tiny tension along a radius from the center of the Earth, and a tiny compression in the orthogonal directions. Just as in Newtonian gravitation, this tidal field typically decays like
, where is the distance from the object.If the object is rotating about some axis, in addition to the tidal effects, there will be various gravitomagnetic
Gravitomagnetism
Gravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
effects, such as spin-spin forces on gyroscopes carried by an observer. In the Kerr vacuum
Kerr metric
The Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
, which is the best known example of type D vacuum solution, this part of the field decays like
.Type III regions are associated with a kind of longitudinal
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
gravitational radiation. In such regions, the tidal forces have a shearing effect. This possibility is often neglected, in part because the gravitational radiation which arises in weak-field theory is type N, and in part because type III radiation decays like
, which is faster than type N radiation.Type N regions are associated with transverse
Transversality
In mathematics, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency, and plays a role in general position. It formalizes the idea of a generic intersection in differential topology...
gravitational radiation, which is the type astronomers are trying to detect with LIGO
LIGO
LIGO, which stands for the Laser Interferometer Gravitational-Wave Observatory, is a large-scale physics experiment aiming to directly detect gravitational waves. Cofounded in 1992 by Kip Thorne and Ronald Drever of Caltech and Rainer Weiss of MIT, LIGO is a joint project between scientists at MIT,...
.
The quadruple principal null direction corresponds to the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
describing the direction of propagation of this radiation. It typically decays like
, so the long-range radiation field is type N.Type II regions combine the effects noted above for types D, III, and N, in a rather complicated nonlinear way.
Type O regions, or conformally flat
Conformally flat
A Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.More formally, let be a pseudo-Riemannian manifold...
regions, are associated with places where the Weyl tensor vanishes identically. In this case, the curvature is said to be pure Ricci. In a conformally flat region, any gravitational effects must be due to the immediate presence of matter or the field
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of some nongravitational field (such as an electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
). In a sense, this means that any distant objects are not exerting any long range influence on events in our region. More precisely, if there are any time varying gravitational fields in distant regions, the news has not yet reached our conformally flat region.
Gravitational radiation emitted from an isolated system will usually not be algebraically special.
The peeling theorem describes the way in which, as one moves farther way from the source of the radiation, the various components of the radiation field "peel" off, until finally only type N radiation is noticeable at large distances. This is similar to the electromagnetic peeling theorem.
Examples
In some (more or less) familiar solutions, the Weyl tensor has the same Petrov type at each event:- the Kerr vacuumKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
is everywhere type D, - certain Robinson/Trautman vacuums are everywhere type III,
- the pp-wave spacetimes are everywhere type N,
- the FRW models are everywhere type O.
More generally, any spherically symmetric spacetime
Spherically symmetric spacetime
A spherically symmetric spacetime is a spacetime whose isometry group contains a subgroup which is isomorphic to the group SO and the orbits of this group are 2-dimensional spheres . The isometries are then interpreted as rotations and a spherically symmetric spacetime is often described as one...
must be of type D (or O). All algebraically special spacetimes having various types of stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
are known, for example, all the type D vacuum solutions.
Some classes of solutions can be invariantly characterized using algebraic symmetries of the Weyl tensor: for example, the class of non-conformally flat null electrovacuum
Electrovacuum solution
In general relativity, an electrovacuum solution is an exact solution of the Einstein field equation in which the only nongravitational mass-energy present is the field energy of an electromagnetic field, which must satisfy the source-free Maxwell equations appropriate to the given geometry...
or null dust
Null dust solution
In mathematical physics, a null dust solution is a Lorentzian manifold in which the Einstein tensor is null...
solutions admitting an expanding but nontwisting null congruence is precisely the class of Robinson/Trautmann spacetimes. These are usually type II, but include type III and type N examples.
Generalization to higher dimensions
A. Coley, R. Milson, V. Pravda and A. Pravdová (2004) developed a generalization of algebraic classification to arbitrary spacetime dimension. Their approach uses a null frame basis approach, that is a frame basis containing two null vectors and , along with spacelike vectors. Frame basis components of the Weyl tensorWeyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
are classified by their transformation properties under local Lorentz boosts. If particular Weyl components vanish, then
and/or are said to be Weyl-Aligned Null Directions (WANDs). In four dimensions, is a WAND if and only if it is a principal null direction in the sense defined above. This approach gives a natural higher-dimensional extension of each of the various algebraic types II,D etc. defined above.An alternative, but inequivalent, generalization was previously defined by de Smet (2002), based on a spinorial approach. However, the de Smet is restricted to 5 dimensions only.
See also
- Classification of electromagnetic fieldsClassification of electromagnetic fieldsIn differential geometry and theoretical physics, the classification of electromagnetic fields is a pointwise classification of bivectors at each point of a Lorentzian manifold....
- Exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
- Segre classificationSegre classificationThe Segre classification is an algebraic classification of rank two symmetric tensors. The resulting types are then known as Segre types. It is most commonly applied to the energy-momentum tensor and primarily finds application in the classification of exact solutions in general relativity....
- Peeling theorem
- Penrose limit