Period (number)
Encyclopedia
In mathematics
, a period is a number
that can be expressed as an integral
of an algebraic function
over an algebraic domain. Sums and products of periods remain periods, so the periods form a ring
.
gave a survey of periods and introduced some conjectures about them.
inequalities with rational coefficients. More generally a complex number is called a period if its real and imaginary parts are periods.
The values of absolutely convergent integrals of rational function
s with algebraic coefficients, over domains in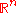
given by polynomial
inequalities with algebraic coefficients are also periods, since integrals and irrational algebraic numbers are expressible in terms of areas of suitable domains.
There are no natural examples of complex numbers that have been proved not to be periods, though it is easy to construct artificial examples using Cantor's diagonal argument
. Plausible candidates for numbers that are not periods include e, 1/π, and Euler's constant γ.
s and the transcendental numbers. The class of algebraic numbers is too narrow to include many common mathematical constant
s, while the set of transcendental numbers is not countable, and its members are not generally computable
. The set of all periods is countable, and all periods are computable, and in particular definable
.
s. Kontsevich and Zagier note that there "seems to be no universal rule explaining why certain infinite sums or integrals of transcendental functions are periods".
Kontsevich and Zagier conjectured that, if a period is given by two different integrals, then each integral can be transformed into the other using only the linearity of integrals, changes of variables
, and the Newton–Leibniz formula
A useful property of algebraic numbers is that equality between two algebraic expressions can be determined algorithmically. The conjecture of Kontsevich and Zagier implies that this is also possible for periods.
It is not expected that Euler's number e and Euler–Mascheroni constant γ are periods. The periods can be extended to exponential periods by permitting the product of an algebraic function and the exponential function
of an algebraic function as an integrand. This extension includes all algebraic powers of e, the gamma function of rational arguments, and values of Bessel function
s. If, further, Euler's constant is added as a new period, then according to Kontsevich and Zagier "all classical constants are periods in the appropriate sense".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a period is a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
that can be expressed as an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of an algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
over an algebraic domain. Sums and products of periods remain periods, so the periods form a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
gave a survey of periods and introduced some conjectures about them.
Definition
A real number is called a period if it is the difference of volumes of regions of Euclidean space given by polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
inequalities with rational coefficients. More generally a complex number is called a period if its real and imaginary parts are periods.
The values of absolutely convergent integrals of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s with algebraic coefficients, over domains in
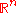given by polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
inequalities with algebraic coefficients are also periods, since integrals and irrational algebraic numbers are expressible in terms of areas of suitable domains.
Examples
Besides the algebraic numbers, the following numbers are known to be periods:- The natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
of any algebraic number -
- Elliptic integralElliptic integralIn integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s with rational arguments - All zeta constantZeta constantIn mathematics, a zeta constant is a number obtained by plugging an integer into the Riemann zeta function. This article provides a number of series identities for the zeta function for integer values.-The Riemann zeta function at 0 and 1:...
s (the Riemann zeta function of an integer) and multiple zeta values - Special values of hypergeometric functions at algebraic arguments
-
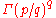for natural numbers p and q, where Γ is the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
.
There are no natural examples of complex numbers that have been proved not to be periods, though it is easy to construct artificial examples using Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
. Plausible candidates for numbers that are not periods include e, 1/π, and Euler's constant γ.
Purpose of the classification
The periods are intended to bridge the gap between the algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s and the transcendental numbers. The class of algebraic numbers is too narrow to include many common mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
s, while the set of transcendental numbers is not countable, and its members are not generally computable
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
. The set of all periods is countable, and all periods are computable, and in particular definable
Definable number
A real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
.
Conjectures
Many of the constants known to be periods are also given by integrals of transcendental functionTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s. Kontsevich and Zagier note that there "seems to be no universal rule explaining why certain infinite sums or integrals of transcendental functions are periods".
Kontsevich and Zagier conjectured that, if a period is given by two different integrals, then each integral can be transformed into the other using only the linearity of integrals, changes of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
, and the Newton–Leibniz formula
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
A useful property of algebraic numbers is that equality between two algebraic expressions can be determined algorithmically. The conjecture of Kontsevich and Zagier implies that this is also possible for periods.
It is not expected that Euler's number e and Euler–Mascheroni constant γ are periods. The periods can be extended to exponential periods by permitting the product of an algebraic function and the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
of an algebraic function as an integrand. This extension includes all algebraic powers of e, the gamma function of rational arguments, and values of Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s. If, further, Euler's constant is added as a new period, then according to Kontsevich and Zagier "all classical constants are periods in the appropriate sense".