Pairing
Encyclopedia
The concept of pairing treated here occurs in mathematics
.
.
A pairing is any R-bilinear map
. That is, it satisfies
,
and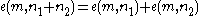 
for any
and any 
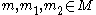and any 
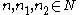. Or equivalently, a pairing is an R-linear map
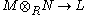
where
denotes the tensor product
of M and N.
A pairing can also be considered as an R-linear map
, which matches the first definition by setting
.
A pairing is called perfect if the above map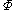
is an isomorphism of R-modules.
If
a pairing is called alternating if for the above map we have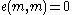 
.
A pairing is called non-degenerate if for the above map we have that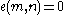
for all 
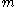implies 
.
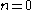The determinant map (2 × 2 matrices over k) → k can be seen as a pairing
.
The Hopf map
written as 
is an example of a pairing. In for instance, Hardie et al. present an explicit construction of the map using poset models.
, often the following specialized definition is used :
Let
be additive groups and 
a multiplicative group
, all of prime order
. Let 
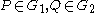be generators
of
and 
respectively.
A pairing is a map:
for which the following holds:
In cases when
, the pairing is called symmetric. Note that is also common in cryptographic literature for all groups to be written in multiplicative notation.
The Weil pairing
is a pairing important in elliptic curve cryptography
; e.g., it may be used to attack certain elliptic curves (see MOV attack). It and other pairings have been used to develop identity-based encryption schemes.
For example, in representation theory
, one has a scalar product on the characters of complex representations of a finite group which is frequently called character pairing.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
.
Definition
Let R be a commutative ring with unity, and let M, N and L be three R-modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
.
A pairing is any R-bilinear map
. That is, it satisfies, and 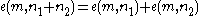for any
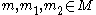and any and any 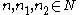. Or equivalently, a pairing is an R-linear map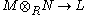where
denotes the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of M and N.
A pairing can also be considered as an R-linear map
, which matches the first definition by setting.A pairing is called perfect if the above map
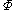is an isomorphism of R-modules.If
a pairing is called alternating if for the above map we have 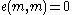.A pairing is called non-degenerate if for the above map we have that
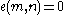for all 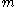implies 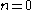.Examples
Any scalar product on a real vector space V is a pairing (set M = N = V, R = R in the above definitions).The determinant map (2 × 2 matrices over k) → k can be seen as a pairing
.The Hopf map
written as is an example of a pairing. In for instance, Hardie et al. present an explicit construction of the map using poset models.Pairings in cryptography
In cryptographyCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, often the following specialized definition is used :
Let
be additive groups and a multiplicative groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, all of prime order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
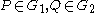. Let be generatorsGenerating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of
and respectively.A pairing is a map:
for which the following holds:
- Bilinearity:
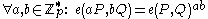
- Non-degeneracy:
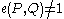
- For practical purposes,
has to be computable in an efficient manner
In cases when
, the pairing is called symmetric. Note that is also common in cryptographic literature for all groups to be written in multiplicative notation.The Weil pairing
Weil pairing
In mathematics, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve E, in such a way as to constitute a pairing on the torsion subgroup of E...
is a pairing important in elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
; e.g., it may be used to attack certain elliptic curves (see MOV attack). It and other pairings have been used to develop identity-based encryption schemes.
Slightly different usages of the notion of pairing
Scalar products on complex vector spaces are sometimes called pairings, although they are not bilinear.For example, in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, one has a scalar product on the characters of complex representations of a finite group which is frequently called character pairing.