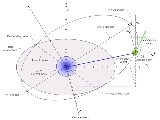
Orbital state vectors
Encyclopedia
In astrodynamics
or celestial dynamics orbital state vectors (sometimes state vectors) are vectors of position ( ) and velocity
) and velocity
( ) that together with their time (epoch
) that together with their time (epoch
) ( ) uniquely determine the state of an orbiting body.
) uniquely determine the state of an orbiting body.
State vectors are excellent for pre-launch orbital predictions when combined with time (epoch) expressed as an offset to the launch time. This makes the state vectors time-independent and good general prediction for orbit
.
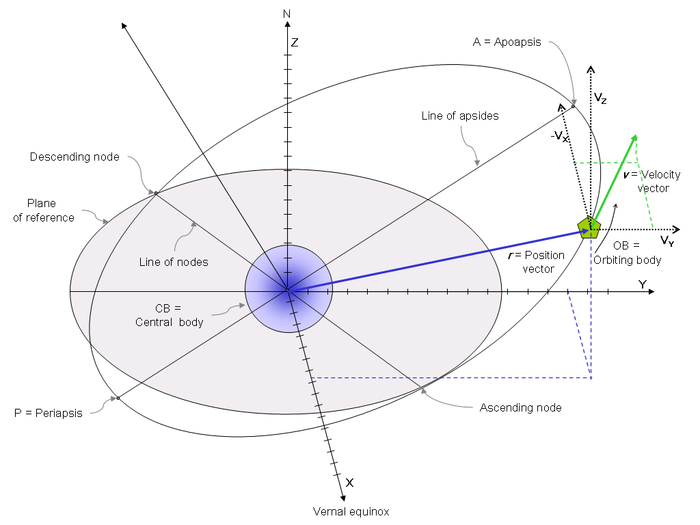
setting. For most practical applications in astrodynamics this is usually assumed to have the following properties:
 is a cartesian
is a cartesian
vector describing the position of the orbiting body in Frame of reference. Together, the orbital position vector and orbital velocity vector describe uniquely the state of an orbiting body and thus are called Orbital state vectors.
 is a cartesian
is a cartesian
vector describing velocity of the orbiting body in frame of reference. Orbital velocity vector together with orbital position vector describe uniquely state of the orbiting body and thus are called Orbital state vectors.
For any object moving through space, the velocity vector is tangent
to the trajectory. If is the unit vector tangent to the trajectory, then
is the unit vector tangent to the trajectory, then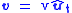
 can be derived from orbital position vector
can be derived from orbital position vector  by differentiation with respect to time:
by differentiation with respect to time:
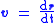
Orbital position is when a planet rotates another planet.
Both state vectors and orbital elements have unique advantages over the other. Computed in advance state vectors are more useful for orbital prediction. A time-independent state vector can be combined with the launch time using xxx method in order to arrive at a valid set of orbital elements whereas computed in advance orbital elements are valid only when launch occurs without the slip.
In astrodynamics
orbital state vectors ( and
and  ) are used with the help of following auxiliary vector:
) are used with the help of following auxiliary vector:
Orbital state vectors can then be used to calculate following orbital elements
(Keplerian elements) (see their definitions for directions):
together with time ( ) (epoch
) (epoch
) those can be used to compute other orbit's parameters:
Keplerian elements typically define an osculating orbit
because of perturbations in the orbital path. The osculating orbit is valid only at the epoch of the original Cartesian elements.
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
or celestial dynamics orbital state vectors (sometimes state vectors) are vectors of position (
 ) and velocity
) and velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
(
 ) that together with their time (epoch
) that together with their time (epochEpoch (astronomy)
In astronomy, an epoch is a moment in time used as a reference point for some time-varying astronomical quantity, such as celestial coordinates, or elliptical orbital elements of a celestial body, where these are subject to perturbations and vary with time...
) (
 ) uniquely determine the state of an orbiting body.
) uniquely determine the state of an orbiting body.State vectors are excellent for pre-launch orbital predictions when combined with time (epoch) expressed as an offset to the launch time. This makes the state vectors time-independent and good general prediction for orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
.

Frame of reference
The state vectors must be considered in a particular inertial frame of referenceInertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
setting. For most practical applications in astrodynamics this is usually assumed to have the following properties:
- cartesian right-handed coordinate system:
- with x-axis pointing to vernal equinox,
- with z-axis pointing upwards, meaning the x-y plane is the reference plane.
Position vector
The orbital position vector is a cartesian
is a cartesianCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
vector describing the position of the orbiting body in Frame of reference. Together, the orbital position vector and orbital velocity vector describe uniquely the state of an orbiting body and thus are called Orbital state vectors.
Velocity vector
Orbital velocity vector is a cartesian
is a cartesianCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
vector describing velocity of the orbiting body in frame of reference. Orbital velocity vector together with orbital position vector describe uniquely state of the orbiting body and thus are called Orbital state vectors.
For any object moving through space, the velocity vector is tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the trajectory. If
 is the unit vector tangent to the trajectory, then
is the unit vector tangent to the trajectory, then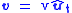
Derivation
Orbital velocity vector can be derived from orbital position vector
can be derived from orbital position vector  by differentiation with respect to time:
by differentiation with respect to time: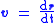
Orbital position is when a planet rotates another planet.
Both state vectors and orbital elements have unique advantages over the other. Computed in advance state vectors are more useful for orbital prediction. A time-independent state vector can be combined with the launch time using xxx method in order to arrive at a valid set of orbital elements whereas computed in advance orbital elements are valid only when launch occurs without the slip.
In astrodynamics
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
orbital state vectors (
 and
and  ) are used with the help of following auxiliary vector:
) are used with the help of following auxiliary vector:
- specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
vector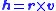
Orbital state vectors can then be used to calculate following orbital elements
Orbital elements
Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are generally considered in classical two-body systems, where a Kepler orbit is used...
(Keplerian elements) (see their definitions for directions):
- InclinationInclinationInclination in general is the angle between a reference plane and another plane or axis of direction.-Orbits:The inclination is one of the six orbital parameters describing the shape and orientation of a celestial orbit...
(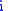 )
) - Eccentricity (
 )
) - Longitude of ascending node (
 )
) - Argument of periapsisArgument of periapsisThe argument of periapsis , symbolized as ω, is one of the orbital elements of an orbiting body...
( )
) - Mean anomalyMean anomalyIn celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....
( )
) - Orbital periodOrbital periodThe orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
( )
)
together with time (
 ) (epoch
) (epochEpoch (astronomy)
In astronomy, an epoch is a moment in time used as a reference point for some time-varying astronomical quantity, such as celestial coordinates, or elliptical orbital elements of a celestial body, where these are subject to perturbations and vary with time...
) those can be used to compute other orbit's parameters:
- True anomalyTrue anomalyIn celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...
( )
) - Semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
( )
) - Semi-minor axisSemi-minor axisIn geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
( )
) - Beta AngleBeta angleThe beta angle is a value that is used most notably in spaceflight. The beta angle determines the percentage of time an object such as a spacecraft in low Earth orbit spends in direct sunlight, absorbing solar energy. Beta angle is defined as the angle between the orbit plane and the vector from...
(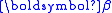 )
) - Linear eccentricityEccentricity (mathematics)In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
( )
) - Periapsis distance (
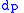 )
) - Apoapsis distance (
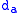 )
) - Eccentric anomalyEccentric anomalyIn celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...
( )
) - Mean longitudeMean longitudeIn astrodynamics or celestial dynamics, mean longitude is the longitude at which an orbiting body could be found if its orbit were circular, and free of perturbations, and if its inclination were zero. Both the mean longitude and the true longitude of the body in such an orbit would change at a...
( )
) - True longitudeTrue longitudeIn astrodynamics true longitude is the longitude at which an orbiting body could actually be found if its inclination were zero. Together with the inclination and the ascending node, the true longitude can tell us the precise direction from the central object at which the body would be located at...
( )
)
Keplerian elements typically define an osculating orbit
Osculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space is the gravitational Kepler orbit In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space (at a given moment of time) is the gravitational Kepler orbit In astronomy,...
because of perturbations in the orbital path. The osculating orbit is valid only at the epoch of the original Cartesian elements.

