In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the nine-point circle is a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

 that can be constructed for any given triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

. It is so named because it passes through nine significant points

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

 defined from the triangle. These nine points are:

• The midpoint
  Midpoint
  The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
  
   of each side of the triangle
  Triangle
  A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
  
  
• The foot of each altitude
  Altitude (triangle)
  In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
  
  
• The midpoint
  Midpoint
  The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
  
   of the line segment
  Line segment
  In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
  
   from each vertex
  Vertex (geometry)
  In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
  
   of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes).

The nine-point circle is also known as Feuerbach's circle, Euler's circle, Terquem's circle, the six-points circle, the twelve-points circle, the n-point circle, the medioscribed circle, the mid circle or the circum-midcircle.

Significant points

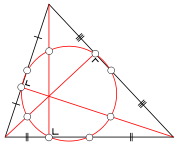
The diagram above shows the nine significant points

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

 of the nine-point circle. Points D, E, and F are the midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

s of the three sides of the triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

. Points G, H, and I are the feet of the altitudes

Altitude (triangle)

In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...

 of the triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

. Points J, K, and L are the midpoint

Midpoint

The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...

s of the line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

s between each altitude's

Altitude (triangle)

In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...

 vertex

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 intersection (points A, B, and C) and the triangle's

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

 orthocenter (point S).

For an acute triangle, six of the points (the midpoints and altitude feet) lie on the triangle itself; for an obtuse triangle two of the altitudes have feet outside the triangle, but these feet still belong to the nine-point circle.

Discovery

Although he is credited for its discovery, Karl Wilhelm Feuerbach

Karl Wilhelm Feuerbach

Karl Wilhelm von Feuerbach was a German geometer and the son of legal scholar Paul Johann Anselm Ritter von Feuerbach, and the brother of philosopher Ludwig Feuerbach. After receiving his doctorate at age 22, he became a professor of mathematics at the Gymnasium at Erlangen...

 did not entirely discover the nine-point circle, but rather the six point circle, recognizing the significance of the midpoints of the three sides of the triangle and the feet of the altitudes of that triangle. (See Fig. 1, points D, E, F, G, H, and I.) (At a slightly earlier date, Charles Brianchon and Jean-Victor Poncelet

Jean-Victor Poncelet

Jean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...

 had stated and proven the same theorem.) But soon after Feuerbach, mathematician Olry Terquem

Olry Terquem

Olry Terquem was a French mathematician, best known for his work in geometry, where he proved Feuerbach's theorem about the nine-point circle of a triangle...

 himself proved the existence of the circle. He was the first to recognize the added significance of the three midpoints between the triangle's vertices and the orthocenter. (See Fig. 1, points J, K, and L.) Thus, Terquem was the first to use the name nine-point circle.

Tangent circles

In 1822 Karl Feuerbach discovered that any triangle's nine-point circle is externally tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

 to that triangle's three excircles and internally tangent to its incircle; this result is known as Feuerbach's theorem. He postulated that:

... the circle which passes through the feet of the altitudes of a triangle is tangent to all four circles which in turn are tangent to the three sides of the triangle...

The point at which the incircle and the nine-point circle touch is often referred to as the Feuerbach point.

Other interesting facts

• The radius of a triangle's circumcircle is twice the radius of that triangle's nine-point circle.

Figure 3

• A nine-point circle bisects a line segment going from the corresponding triangle's orthocenter to any point
  Point (geometry)
  In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
  
   on its circumcircle.

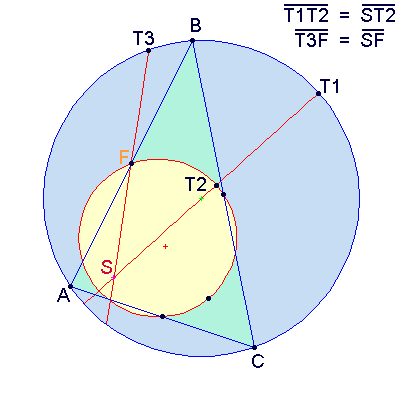
Figure 4

• The center of any nine-point circle (the nine-point center) lies on the corresponding triangle's Euler line
  Euler's line
  In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral; it passes through several important points determined from the triangle...
  
  , at the midpoint
  Midpoint
  The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
  
   between that triangle's orthocenter and circumcenter.

• The nine-point center lies at the centroid
  Centroid
  In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
  
   of four points comprising the triangle's three vertices and its orthocenter.

• Of the nine points, the three midpoints of line segments between the vertices and the orthocenter are reflections of the triangle's midpoints about its nine-point center.

• The center of all rectangular hyperbolas that pass through the vertices of a triangle lies on its nine-point circle. Examples include the well-known rectangular hyperbolas of Keipert, Jeřábek and Feuerbach. This fact is known as the Feuerbach conic theorem.

• If an orthocentric system
  Orthocentric system
  In geometry, an orthocentric system is a set of four points in the plane one of which is the orthocenter of the triangle formed by the other three....
  
   of four points
  Point (geometry)
  In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
  
   A, B, C and H is given, then the four triangle
  Triangle
  A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
  
  s formed by any combination of three distinct points
  Point (geometry)
  In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
  
   of that system all share the same nine-point circle. Consequently, these four triangles have circumcircles with identical radii. Let N represent the common nine-point center and P be an arbitrary point in the plane of the orthocentric system. Then NA²+NB²+NC²+NH² = 3R² where R is the common circumradius and if PA²+PB²+PC²+PH² = K², where K is kept constant, then the locus of P is a circle centered at N with a radius . As P approaches N the locus of P for the corresponding constant K, collapses onto N the nine-point center. Furthermore the nine-point circle is the locus of P such that PA²+PB²+PC²+PH² = 4R².

• The centers of the incircle and excircles of a triangle form an orthocentric system. The nine-point circle created for that orthocentric system is the circumcircle of the original triangle. The feet of the altitudes in the orthocentric system are the vertices of the original triangle.

• If four arbitrary points A, B, C, D are given that do not form an orthocentric system, then the nine-point circles of ABC, BCD, CDA and DAB concur at a point
  Point (geometry)
  In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
  
  . The remaining six intersection points of these nine-point circles each concur with the midpoints of the four triangles. Remarkably, there exists a unique nine-point conic, centered at the centroid of these four arbitrary points, that passes through all seven points of intersection of these nine-point circles. Furthermore because of the Feuerbach conic theorem mentioned above, there exists a unique rectangular circumconic, centered at the common intersection point of the four nine-point circles, that passes through the four original arbitrary points as well as the orthocenters of the four triangles.

• If four points A, B, C, D are given that form a cyclic quadrilateral
  Cyclic quadrilateral
  In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
  
  , then the nine-point circles of ABC, BCD, CDA and DAB concur at the anticenter of the cyclic quadrilateral. The nine-point circles are all congruent with a radius of half that of the cyclic quadrilateral's circumcircle. The nine-point circles form a set of four Johnson circles
  Johnson circles
  In geometry, a set of Johnson circles comprise three circles of equal radius r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections : the common point H that they all share, and for each of the three pairs of circles one more...
  
  . Consequently the four nine-point centers are cylic and lie on a circle congruent to the four nine-point circles that is centered at the anticenter of the cyclic quadrilateral. Furthermore the cyclic quadrilateral formed from the four nine-pont centers is homothetic to the reference cyclic quadrilateral ABCD by a factor of  −¹/₂  and its homothetic center (N) lies on the line connecting the circumcenter (O) to the anticenter (M) where ON = 2NM.

• The orthopole of lines passing through the circumcenter lie on the nine-point circle.

• Trilinear coordinates
  Trilinear coordinates
  In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
  
   for the nine-point center are cos (B − C) : cos (C − A) : cos (A − B)

• Trilinear coordinates
  Trilinear coordinates
  In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
  
   for the Feuerbach point are 1 − cos (B − C) : 1 − cos (C − A) : 1 − cos (A − B)

• Trilinear coordinates
  Trilinear coordinates
  In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
  
   for the center of the Kiepert hyperbola are (b² − c²)²/a : (c² − a²)²/b : (a² − b²)²/c

• Trilinear coordinates
  Trilinear coordinates
  In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
  
   for the center of the Jeřábek hyperbola are cos A sin²(B − C) : cos B sin²(C − A) : cos C sin²(A − B)

• Letting x : y : z be a variable point in trilinear coordinates
  Trilinear coordinates
  In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
  
  , an equation for the nine-point circle is

x²sin 2A + y²sin 2B + z²sin 2C − 2(yz sin A + zx sin B + xy sin C) = 0.

See also

• Nine-point hyperbola
  Nine-point hyperbola
  -Discovery:The nine-point hyperbola was first discovered by E.F. Allen and his work was published in a volume of The American Mathematical Monthly in December, 1941...
  
  
• Synthetic geometry
  Synthetic geometry
  Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
  
  
• Lester's theorem
  Lester's theorem
  In Euclidean plane geometry, Lester's theorem, named after June Lester, states that in any scalene triangle, the two Fermat points, the nine-point center, and the circumcenter are concyclic.- References :...
  
  
• Triangle center
  Triangle center
  In geometry a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions. Each of...
  
  

External links

• Encyclopedia of Triangles Centers by Clark Kimberling. The nine-point center is indexed as X(5), the Feuerbach point, as X(11), the center of the Kiepert hyperbola as X(115), and the center of the Jeřábek hyperbola as X(125).
• History about the nine-point circle based on J.S. MacKay's article from 1892: History of the Nine Point Circle
• Nine Point Circle in Java at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Feuerbach's Theorem: a Proof at cut-the-knot
  Cut-the-knot
  Cut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
  
  
• Special lines and circles in a triangle by Walter Fendt (requires Java)
• An interactive Java applet showing several triangle centers that lies on the Nine Point Circle.
• Interactive Nine Point Circle applet from the Wolfram Demonstrations Project
• Nine-point conic and Euler line generalization at Dynamic Geometry Sketches Generalizes nine-point circle to a nine-point conic with an associated generalization of the Euler line.