Newton's method in optimization
Encyclopedia
In mathematics
, Newton's method
is an iterative method
for finding roots of equation
s. More generally, Newton's method is used to find critical points
of differentiable function
s, which are the zeros of the derivative
function.
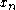from an initial guess 
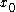that converges towards 
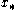such that 
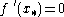. This 
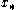is called a stationary point
of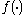
.
The second order Taylor expansion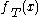
of function 
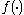around 
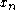(where 
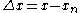) is:
,
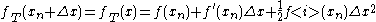attains its extremum when its derivative with respect to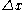
is equal to zero, i.e. when 
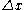solves the linear equation: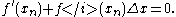
(Considering the right-hand side of the above equation as a quadratic in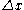
, with constant coefficients.)
Thus, provided that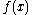
is a twice-differentiable function
well approximated by its second order Taylor expansion and the initial guess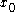
is chosen close enough to 
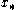, the sequence 
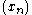defined by:
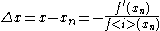
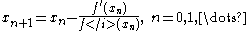
will converge towards a root of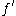
, i.e. 
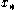for which 
.
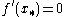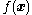by a quadratic function
around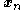
, and then takes a step towards the maximum/minimum of that quadratic function (in higher dimensions, this may also be a saddle point
). Note that if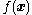
happens to be a quadratic function, then the exact extremum is found in one step.
can be generalized to several dimensions by replacing the derivative with the gradient
,
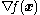, and the reciprocal
of the second derivative with the inverse of the Hessian matrix
,
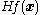. One obtains the iterative scheme
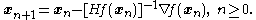
Usually Newton's method is modified to include a small step size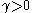
instead of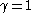 
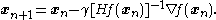
This is often done to ensure that the Wolfe conditions
are satisfied at each step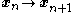
of the iteration.
Where applicable, Newton's method converges much faster towards a local maximum or minimum than gradient descent
. In fact, every local minimum has a neighborhood
such that, if we start with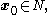 
Newton's method with step size 
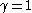converges quadratically
(if the Hessian is invertible and a Lipschitz continuous
function of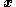
in that neighborhood).
Finding the inverse of the Hessian in high dimensions can be an expensive operation. In such cases, instead of directly inverting the Hessian it's better to calculate the vector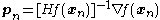
as the solution to the system of linear equations
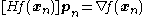
which may be solved by various factorizations or approximately (but to great accuracy) using iterative methods. Many of these methods are only applicable to certain types of equations, for example the Cholesky factorization and conjugate gradient
will only work if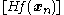
is a positive definite matrix. While this may seem like a limitation, it's often useful indicator of something gone wrong, for example if a minimization problem is being approached and 
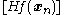is not positive definite, then the iterations are converging to a saddle point
and not a minimum.
On the other hand, if a constrained optimization is done (for example, with Lagrange multipliers
), the problem may become one of saddle point finding, in which case the Hessian will be symmetric indefinite and the solution of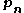
will need to be done with a method that will work for such, such as the LDLT variant of Cholesky factorization or the conjugate residual method
.
There also exist various quasi-Newton method
s, where an approximation for the Hessian (or its inverse directly) is built up from changes in the gradient.
If the Hessian is close to a non-invertible matrix, the inverted Hessian can be numerically unstable and the solution may diverge. In this case, certain workarounds have been tried in the past, which have varied success with certain problems. One can, for example, modify the Hessian by adding a correction matrix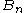
so as to make 
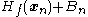positive definite. One approach is to diagonalize 
and choose 
so that 
has the same eigenvectors as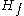 
, but with each negative eigenvalue replaced by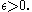 
An approach exploited in the Levenberg–Marquardt algorithm (which uses an approximate Hessian) is to add a scaled identity matrix to the Hessian,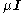
, with the scale adjusted at every iteration as needed. For large 
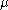and small Hessian, the iterations will behave like gradient descent
with step size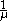
. This results in slower but more reliable convergence where the Hessian doesn't provide useful information.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
is an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for finding roots of equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
s. More generally, Newton's method is used to find critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
of differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s, which are the zeros of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
function.
Method
Newton's Method attempts to construct a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
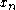from an initial guess 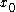that converges towards 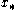such that 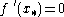. This 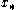is called a stationary pointStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
of
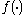.The second order Taylor expansion
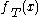of function 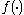around 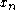(where 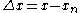) is: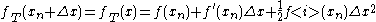,attains its extremum when its derivative with respect to
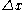is equal to zero, i.e. when 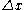solves the linear equation: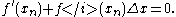(Considering the right-hand side of the above equation as a quadratic in
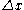, with constant coefficients.)Thus, provided that
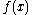is a twice-differentiable functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
well approximated by its second order Taylor expansion and the initial guess
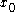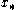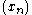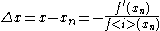
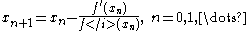
is chosen close enough to , the sequence defined by:will converge towards a root of
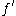, i.e. 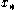for which 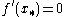.Geometric interpretation
The geometric interpretation of Newton's method is that at each iteration one approximates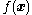 by a quadratic functionQuadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
around
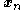, and then takes a step towards the maximum/minimum of that quadratic function (in higher dimensions, this may also be a saddle pointSaddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
). Note that if
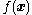happens to be a quadratic function, then the exact extremum is found in one step.Higher dimensions
The above iterative schemeIteration
Iteration means the act of repeating a process usually with the aim of approaching a desired goal or target or result. Each repetition of the process is also called an "iteration," and the results of one iteration are used as the starting point for the next iteration.-Mathematics:Iteration in...
can be generalized to several dimensions by replacing the derivative with the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
,
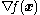, and the reciprocalMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the second derivative with the inverse of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
,
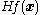. One obtains the iterative scheme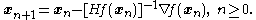Usually Newton's method is modified to include a small step size
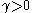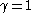
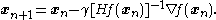
instead of This is often done to ensure that the Wolfe conditions
Wolfe conditions
In the unconstrained minimization problem, the Wolfe conditions are a set of inequalities for performing inexact line search, especially in quasi-Newton methods.In these methods the idea is to find\min_x f...
are satisfied at each step
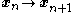of the iteration.Where applicable, Newton's method converges much faster towards a local maximum or minimum than gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
. In fact, every local minimum has a neighborhood
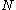such that, if we start with 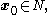Newton's method with step size 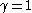converges quadraticallyRate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
(if the Hessian is invertible and a Lipschitz continuous
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
function of
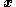in that neighborhood).Finding the inverse of the Hessian in high dimensions can be an expensive operation. In such cases, instead of directly inverting the Hessian it's better to calculate the vector
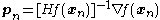as the solution to the system of linear equations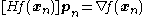which may be solved by various factorizations or approximately (but to great accuracy) using iterative methods. Many of these methods are only applicable to certain types of equations, for example the Cholesky factorization and conjugate gradient
Conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
will only work if
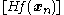is a positive definite matrix. While this may seem like a limitation, it's often useful indicator of something gone wrong, for example if a minimization problem is being approached and 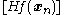is not positive definite, then the iterations are converging to a saddle pointSaddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
and not a minimum.
On the other hand, if a constrained optimization is done (for example, with Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
), the problem may become one of saddle point finding, in which case the Hessian will be symmetric indefinite and the solution of
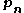will need to be done with a method that will work for such, such as the LDLT variant of Cholesky factorization or the conjugate residual methodConjugate residual method
The conjugate residual method is an iterative numeric method used for solving systems of linear equations. It's a Krylov subspace method very similar to the much more popular conjugate gradient method, with similar construction and convergence properties....
.
There also exist various quasi-Newton method
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
s, where an approximation for the Hessian (or its inverse directly) is built up from changes in the gradient.
If the Hessian is close to a non-invertible matrix, the inverted Hessian can be numerically unstable and the solution may diverge. In this case, certain workarounds have been tried in the past, which have varied success with certain problems. One can, for example, modify the Hessian by adding a correction matrix
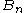so as to make 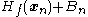positive definite. One approach is to diagonalize 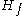and choose 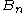so that 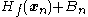has the same eigenvectors as 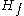, but with each negative eigenvalue replaced by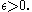 An approach exploited in the Levenberg–Marquardt algorithm (which uses an approximate Hessian) is to add a scaled identity matrix to the Hessian,
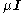, with the scale adjusted at every iteration as needed. For large 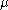and small Hessian, the iterations will behave like gradient descentGradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
with step size
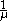. This results in slower but more reliable convergence where the Hessian doesn't provide useful information.Other approximations
Some functions are poorly approximated by quadratics, particularly when far from a maximum or minimum. In these cases, approximations other than quadratic may be more appropriate.See also
- Quasi-Newton methodQuasi-Newton methodIn optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
- Gradient descentGradient descentGradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
- Gauss–Newton algorithm
- Levenberg–Marquardt algorithm
- Trust regionTrust regionTrust region is a term used in mathematical optimization to denote the subset of the region of the objective function to be optimized that is approximated using a model function . If an adequate model of the objective function is found within the trust region then the region is expanded;...
- OptimizationOptimization (mathematics)In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....