Napier's bones
Encyclopedia
Napier's bones is an abacus
created by John Napier
for calculation
of products and quotients of numbers that was based on Arab mathematics and lattice multiplication used by Matrakci Nasuh
in the Umdet-ul Hisab and Fibonacci
writing in the Liber Abaci
. Also called Rabdology (from Greek [], "rod" and [], "study"). Napier published his version of rods in a work printed in Edinburgh
, Scotland
, at the end of 1617 entitled Rabdologiæ. Using the multiplication tables embedded in the rods, multiplication can be reduced to addition operations and division to subtractions. More advanced use of the rods can even extract square root
s. Note that Napier's bones are not the same as logarithm
s, with which Napier's name is also associated.
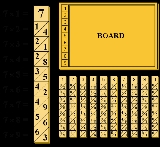
The abacus consists of a board with a rim; the user places Napier's rods in the rim to conduct multiplication or division. The board's left edge is divided into 9 squares, holding the numbers 1 to 9. The Napier's rods consist of strips of wood, metal or heavy cardboard. Napier's bones are three dimensional, square in cross section, with four different rods engraved on each one. A set of such bones might be enclosed in a convenient carrying case.
A rod's surface comprises 9 squares, and each square, except for the top one, comprises two halves divided by a diagonal line. The first square of each rod holds a single digit, and the other squares hold this number's double, triple, quadruple, quintuple, and so on until the last square contains nine times the number in the top square. The digits of each product are written one to each side of the diagonal; numbers less than 10 occupy the lower triangle, with a zero in the top half.
A set consists of 10 rods corresponding to digits 0 to 9. The rod 0, although it may look unnecessary, is obviously still needed for multipliers or multiplicands having 0 in them.
From right to left, we obtain the units place (3), the tens (6+3=9), the hundreds (6+1=7), etc. Note that in the hundred thousands place, where 5+9=14, we note '4' and carry '1' to the next addition (similarly with 4+8=12 in the ten millions place).
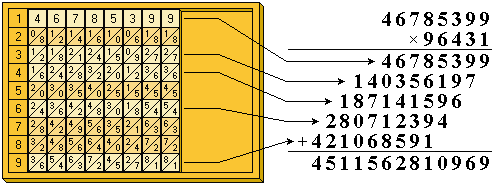
In cases where a digit of the multiplicand is 0, we leave a space between the rods corresponding to where a 0 rod would be. Let us suppose that we want to multiply the previous number by 96431; operating analogously to the previous case, we will calculate partial products of the number by multiplying 46785399 by 9, 6, 4, 3 and 1. Then we place these products in the appropriate positions, and add them using the simple pencil-and-paper method.
This method can also be used for multiplying decimals. For a decimal value multiplied by an integer (whole number) value ensure that the decimal number is written along the top of the grid. From this position the decimal point simply drops down the vertical line and 'falls' into the answer.
When multiplying two decimal numbers together, the decimal points travel horizontally and vertically until they 'meet' at a diagonal line, the point then travels out of the grid in the same method and again 'falls' into the answer.
The form of multiplication was also used in the 1202 Liber Abaci
and 800 AD Islamic mathematics and known under the name of lattice multiplication. "Crest of the Peacock", by G.G, Joseph, suggests that Napier learned the details of this method from "Treviso Arithmetic
", written in 1499....
number left is the remainder.

So in this example, we get a quotient of 485 with a remainder of 16364. We can just stop here and
use the fractional form of the answer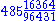 .
.
If you prefer, we can also find as many decimal points as we need by continuing the cycle as in
standard long division
. Mark a decimal point after the last digit of the quotient and append a zero
to the remainder so we now have 163640. Continue the cycle, but each time appending a zero to the
result after the subtraction.
Let's work through a couple of digits. The first digit after the decimal point is
1, because the biggest partial product less than 163640 is
96431, from row 1. Subtracting 96431 from 163640, we're left with 67209.
Appending a zero, we have 672090 to consider for the next cycle (with the partial result
485.1)
The second digit after the decimal point is 6, as the biggest partial product less
than 672090 is 578586 from row 6. The partial result is now 485.16, and so on.

different from the others as it has three columns on it. The first
column has the first nine squares 1, 4, 9, ... 64, 81, the second
column has the even numbers 2 through 18, and the last column just has
the numbers 1 through 9.
Let's find the square root of 46785399 with the bones.
First, group its digits in twos starting from the right so it looks
like this:
Start with the leftmost group 46. Pick the largest square on the
square root bone less than 46, which is 36 from the sixth row.
Because we picked the sixth row, the first digit of the solution is 6.
Now read the second column from the sixth row on the square root bone,
12, and set 12 on the board.
Then subtract the value in the first
column of the sixth row, 36, from 46.
Append to this the next group of
digits in the number 78, to get the remainder 1078.
At the end of this step, the board and intermediate calculations
should look like this:
Now, "read" the numbers in each row, ignoring the second and third columns
from the square root bone and record these. (For example, read the sixth
row as : 0/6 1/2 3/6 → 756)
Find the largest number less than the current remainder, 1078.
You should find that 1024 from the eighth row is the largest value
less than 1078.
As before, append 8 to get the next digit of the square root and
subtract the value of the eighth row 1024 from the current remainder
1078 to get 54. Read the second column of the eighth row on the square
root bone, 16, and set the number on the board as follows.
The current number on the board is 12. Add to it the first digit of
16, and append the second digit of 16 to the result. So you should set
the board to
The board and intermediate calculations now look like this.
Once again, find the row with the largest value less than the current
partial remainder 5453. This time, it is the third row with 4089.
The next digit of the square root is 3. Repeat the same steps as
before and subtract 4089 from the current remainder 5453 to get 1364
as the next remainder. When you rearrange the board, notice that the
second column of the square root bone is 6, a single digit. So just
append 6 to the current number on the board 136
to set 1366 on the board.
Repeat these operations once more. Now the largest value on the board
smaller than the current remainder 136499 is 123021 from the ninth
row.
In practice, you often don't need to find the value of every row to
get the answer. You may be able to guess which row has the answer by
looking at the number on the first few bones on the board and
comparing it with the first few digits of the remainder. But in these
diagrams, we show the values of all rows to make it easier to
understand.
As usual, append a 9 to the result and subtract 123021 from the
current remainder.
You've now "used up" all the digits of our number, and you still have
a remainder. This means you've got the integer portion of the square
root but there's some fractional bit still left.
Notice that if we've really got the integer part of the square root,
the current result squared (6839² = 46771921) must be the
largest perfect square smaller than 46785899. Why? The square root of
46785399 is going to be something like 6839.xxxx... This means
6839² is smaller than 46785399, but 6840² is
bigger than 46785399—the same thing as saying that 6839²
is the largest perfect square smaller than 46785399.
This idea is used later on to understand how the technique works, but
for now let's continue to generate more digits of the square root.
Similar to finding the fractional portion of the answer in
long division
, append two zeros to the remainder to get
the new remainder 1347800. The second column of the ninth row of the
square root bone is 18 and the current number on the board is 1366. So
compute
to set 13678 on the board.
The board and intermediate computations now look like this.
The ninth row with 1231101 is the largest value smaller than the
remainder, so the first digit of the fractional part of the square
root is 9.
Subtract the value of the ninth row from the remainder and append a
couple more zeros to get the new remainder 11669900. The second column
on the ninth row is 18 with 13678 on the board, so compute
and set 136798 on the board.
You can continue these steps to find as many digits as you need and
you stop when you have the precision you want, or if you find that the
reminder becomes zero which means you have the exact square root.
Having found the desired number of digits, you can easily determine whether or not you need to round up; i.e., increment the last digit. You don't need to find another digit to see if it is equal to or greater than five. Simply append 25 to the root and compare that to the remainder; if it is less than or equal to the remainder, then the next digit will be at least five and round up is needed. In the example above, we see that 6839925 is less than 11669900, so we need to round up the root to 6840.0.
There's only one more trick left to describe. If you want to find the
square root of a number that isn't an integer, say 54782.917.
Everything is the same, except you start out by grouping the digits
to the left and right of the decimal point in groups of two.
That is, group 54782.917 as
and proceed to extract the square root from these groups of digits.
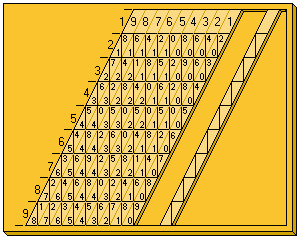
The rods were made such that the vertical and horizontal lines were more visible than the line where the rods touched, making the two components of each digit of the result much easier to read. Thus, in the picture it is immediately clear that:
The following example is calculating 52749 × 4 = 210996.
National Archaeological Museum
, in Madrid
.
The apparatus is a box of wood
with inlays of bone
. In the top section it contains the "bones" abacus, and in the bottom section is the card abacus. This card abacus consists of 300 stored cards in 30 drawers. One hundred of these cards are covered with numbers (referred to as the "number cards"). The remaining two hundred cards contain small triangular holes, which, when laid on top of the number cards, allow the user to see only certain numbers. By the capable positioning of these cards, multiplications can be made up to the limit of a number 100 digits in length, by another number 200 digits in length.
In addition, the doors of the box contain the first powers of the digits, the coefficients of the terms of the first powers of the binomial
and the numeric data of the regular polyhedra
.
It is not known who was the author of this piece, nor if it is of Spanish origin or came from a foreigner, although it is probable that it originally belonged to the Spanish Academy of Mathematics
(which was created by Philip II
) or was a gift from the Prince of Wales
. The only thing that is sure is that it was conserved in the Palace, of where it was passed to the National library
and later to the National Archaeological Museum, where it is still conserved.
In 1876, the Spanish government sent the apparatus to the exhibition of scientific instruments celebrated in Kensington
, where it received much attention, up to the point at which several societies consulted the Spanish representation about the origin and use of the apparatus. This motivated D. Felipe Picatoste to write a monograph, that was sent to all the nations, in which he expressed surprise about the fact that the abacus was only well-known in "England
, country of origin of its inventor" (though of course he originated in Scotland
).
Abacus
The abacus, also called a counting frame, is a calculating tool used primarily in parts of Asia for performing arithmetic processes. Today, abaci are often constructed as a bamboo frame with beads sliding on wires, but originally they were beans or stones moved in grooves in sand or on tablets of...
created by John Napier
John Napier
John Napier of Merchiston – also signed as Neper, Nepair – named Marvellous Merchiston, was a Scottish mathematician, physicist, astronomer & astrologer, and also the 8th Laird of Merchistoun. He was the son of Sir Archibald Napier of Merchiston. John Napier is most renowned as the discoverer...
for calculation
Calculation
A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...
of products and quotients of numbers that was based on Arab mathematics and lattice multiplication used by Matrakci Nasuh
Matrakçi Nasuh
Nasuh bin Karagöz bin Abdullah el-Bosnavî , commonly known as Matrakçı Nasuh for his competence in the game called Matrak was a 16th century Ottoman mathematician, teacher, historian, geographer, cartographer, swordmaster, and miniaturist of...
in the Umdet-ul Hisab and Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
writing in the Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
. Also called Rabdology (from Greek [], "rod" and [], "study"). Napier published his version of rods in a work printed in Edinburgh
Edinburgh
Edinburgh is the capital city of Scotland, the second largest city in Scotland, and the eighth most populous in the United Kingdom. The City of Edinburgh Council governs one of Scotland's 32 local government council areas. The council area includes urban Edinburgh and a rural area...
, Scotland
Scotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
, at the end of 1617 entitled Rabdologiæ. Using the multiplication tables embedded in the rods, multiplication can be reduced to addition operations and division to subtractions. More advanced use of the rods can even extract square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s. Note that Napier's bones are not the same as logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s, with which Napier's name is also associated.
The abacus consists of a board with a rim; the user places Napier's rods in the rim to conduct multiplication or division. The board's left edge is divided into 9 squares, holding the numbers 1 to 9. The Napier's rods consist of strips of wood, metal or heavy cardboard. Napier's bones are three dimensional, square in cross section, with four different rods engraved on each one. A set of such bones might be enclosed in a convenient carrying case.
A rod's surface comprises 9 squares, and each square, except for the top one, comprises two halves divided by a diagonal line. The first square of each rod holds a single digit, and the other squares hold this number's double, triple, quadruple, quintuple, and so on until the last square contains nine times the number in the top square. The digits of each product are written one to each side of the diagonal; numbers less than 10 occupy the lower triangle, with a zero in the top half.
A set consists of 10 rods corresponding to digits 0 to 9. The rod 0, although it may look unnecessary, is obviously still needed for multipliers or multiplicands having 0 in them.
Multiplication
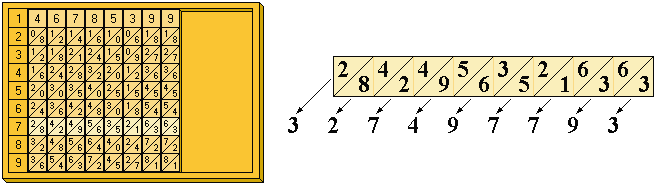
Given the described set of rods, suppose that we wish to calculate the product of 46785399 and 7. Place inside the board the rods corresponding to 46785399, as shown in the diagram, and read the result in the horizontal strip in row 7, as marked on the side of the board. To obtain the product, simply note, for each place from right to left, the numbers found by adding the digits within the diagonal sections of the strip (using carry-over where the sum is 10 or greater).
From right to left, we obtain the units place (3), the tens (6+3=9), the hundreds (6+1=7), etc. Note that in the hundred thousands place, where 5+9=14, we note '4' and carry '1' to the next addition (similarly with 4+8=12 in the ten millions place).
In cases where a digit of the multiplicand is 0, we leave a space between the rods corresponding to where a 0 rod would be. Let us suppose that we want to multiply the previous number by 96431; operating analogously to the previous case, we will calculate partial products of the number by multiplying 46785399 by 9, 6, 4, 3 and 1. Then we place these products in the appropriate positions, and add them using the simple pencil-and-paper method.

This method can also be used for multiplying decimals. For a decimal value multiplied by an integer (whole number) value ensure that the decimal number is written along the top of the grid. From this position the decimal point simply drops down the vertical line and 'falls' into the answer.
When multiplying two decimal numbers together, the decimal points travel horizontally and vertically until they 'meet' at a diagonal line, the point then travels out of the grid in the same method and again 'falls' into the answer.
The form of multiplication was also used in the 1202 Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
and 800 AD Islamic mathematics and known under the name of lattice multiplication. "Crest of the Peacock", by G.G, Joseph, suggests that Napier learned the details of this method from "Treviso Arithmetic
Treviso Arithmetic
The Treviso Arithmetic, or Arte dell'Abbaco, is an anonymous textbook in commercial arithmetic written in vernacular Venetian and published in Treviso, Italy in 1478.The author tells us the reason for writing this textbook:...
", written in 1499....
Division
Division can be performed in a similar fashion. Let's divide 46785399 by 96431, the two numbers we used in the earlier example. Put the bars for the divisor (96431) on the board, as shown in the graphic below. Using the abacus, find all the products of the divisor from 1 to 9 by reading the displayed numbers. Note that the dividend has eight digits, whereas the partial products (save for the first one) all have six. So you must temporarily ignore the final two digits of 46785399, namely the '99', leaving the number 467853. Next, look for the greatest partial product that is less than the truncated dividend. In this case, it's 385724. You must mark down two things, as seen in the diagram: since 385724 is in the '4' row of the abacus, mark down a '4' as the left-most digit of the quotient; also write the partial product, left-aligned, under the original dividend, and subtract the two terms. You get the difference as 8212999. Repeat the same steps as above: truncate the number to six digits, chose the partial product immediately less than the truncated number, write the row number as the next digit of the quotient, and subtract the partial product from the difference found in the first repetition. Following the diagram should clarify this. Repeat this cycle until the result of subtraction is less than the divisor. Thenumber left is the remainder.

So in this example, we get a quotient of 485 with a remainder of 16364. We can just stop here and
use the fractional form of the answer
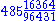 .
.If you prefer, we can also find as many decimal points as we need by continuing the cycle as in
standard long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
. Mark a decimal point after the last digit of the quotient and append a zero
to the remainder so we now have 163640. Continue the cycle, but each time appending a zero to the
result after the subtraction.
Let's work through a couple of digits. The first digit after the decimal point is
1, because the biggest partial product less than 163640 is
96431, from row 1. Subtracting 96431 from 163640, we're left with 67209.
Appending a zero, we have 672090 to consider for the next cycle (with the partial result
485.1)
The second digit after the decimal point is 6, as the biggest partial product less
than 672090 is 578586 from row 6. The partial result is now 485.16, and so on.

Extracting square roots
Extracting the square root uses an additional bone which looks a bitdifferent from the others as it has three columns on it. The first
column has the first nine squares 1, 4, 9, ... 64, 81, the second
column has the even numbers 2 through 18, and the last column just has
the numbers 1 through 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | ||
| 1 | 0/1 | 0/2 | 0/3 | 0/4 | 0/5 | 0/6 | 0/7 | 0/8 | 0/9 | 0/1 2 1 | |
| 2 | 0/2 | 0/4 | 0/6 | 0/8 | 1/0 | 1/2 | 1/4 | 1/6 | 1/8 | 0/4 4 2 | |
| 3 | 0/3 | 0/6 | 0/9 | 1/2 | 1/5 | 1/8 | 2/1 | 2/4 | 2/7 | 0/9 6 3 | |
| 4 | 0/4 | 0/8 | 1/2 | 1/6 | 2/0 | 2/4 | 2/8 | 3/2 | 3/6 | 1/6 8 4 | |
| 5 | 0/5 | 1/0 | 1/5 | 2/0 | 2/5 | 3/0 | 3/5 | 4/0 | 4/5 | 2/5 10 5 | |
| 6 | 0/6 | 1/2 | 1/8 | 2/4 | 3/0 | 3/6 | 4/2 | 4/8 | 5/4 | 3/6 12 6 | |
| 7 | 0/7 | 1/4 | 2/1 | 2/8 | 3/5 | 4/2 | 4/9 | 5/6 | 6/3 | 4/9 14 7 | |
| 8 | 0/8 | 1/6 | 2/4 | 3/2 | 4/0 | 4/8 | 5/6 | 6/4 | 7/2 | 6/4 16 8 | |
| 9 | 0/9 | 1/8 | 2/7 | 3/6 | 4/5 | 5/4 | 6/3 | 7/2 | 8/1 | 8/1 18 9 |
Let's find the square root of 46785399 with the bones.
First, group its digits in twos starting from the right so it looks
like this:
- 46 78 53 99
- Note: A number like 85399 would be grouped as 8 53 99
Start with the leftmost group 46. Pick the largest square on the
square root bone less than 46, which is 36 from the sixth row.
Because we picked the sixth row, the first digit of the solution is 6.
Now read the second column from the sixth row on the square root bone,
12, and set 12 on the board.
Then subtract the value in the first
column of the sixth row, 36, from 46.
Append to this the next group of
digits in the number 78, to get the remainder 1078.
At the end of this step, the board and intermediate calculations
should look like this:
EWLINE
|
_____________ √46 78 53 99 = 6 36—10 78 |
Now, "read" the numbers in each row, ignoring the second and third columns
from the square root bone and record these. (For example, read the sixth
row as : 0/6 1/2 3/6 → 756)
Find the largest number less than the current remainder, 1078.
You should find that 1024 from the eighth row is the largest value
less than 1078.
EWLINE
|
_____________ √46 78 53 99 = 68 36—10 78 10 24 ----- 54 |
As before, append 8 to get the next digit of the square root and
subtract the value of the eighth row 1024 from the current remainder
1078 to get 54. Read the second column of the eighth row on the square
root bone, 16, and set the number on the board as follows.
The current number on the board is 12. Add to it the first digit of
16, and append the second digit of 16 to the result. So you should set
the board to
- 12 + 1 = 13 → append 6 → 136
- Note: If the second column of the square root bone has only one digit, just append it to the current number on board.
The board and intermediate calculations now look like this.
EWLINE
|
_____________ √46 78 53 99 = 68 36—10 78 10 24 ----- 54 53 |
Once again, find the row with the largest value less than the current
partial remainder 5453. This time, it is the third row with 4089.
EWLINE
|
_____________ √46 78 53 99 = 683 36—10 78 10 24 ----- 54 53 40 89 ----- 13 64 |
The next digit of the square root is 3. Repeat the same steps as
before and subtract 4089 from the current remainder 5453 to get 1364
as the next remainder. When you rearrange the board, notice that the
second column of the square root bone is 6, a single digit. So just
append 6 to the current number on the board 136
- 136 → append 6 → 1366
to set 1366 on the board.
EWLINE
|
_____________ √46 78 53 99 = 683 36—10 78 10 24 ----- 54 53 40 89 ----- 13 64 99 |
Repeat these operations once more. Now the largest value on the board
smaller than the current remainder 136499 is 123021 from the ninth
row.
In practice, you often don't need to find the value of every row to
get the answer. You may be able to guess which row has the answer by
looking at the number on the first few bones on the board and
comparing it with the first few digits of the remainder. But in these
diagrams, we show the values of all rows to make it easier to
understand.
As usual, append a 9 to the result and subtract 123021 from the
current remainder.
EWLINE
|
_____________ √46 78 53 99 = 6839 36—10 78 10 24 ----- 54 53 40 89 ----- 13 64 99 12 30 21 -------- 1 34 78 |
You've now "used up" all the digits of our number, and you still have
a remainder. This means you've got the integer portion of the square
root but there's some fractional bit still left.
Notice that if we've really got the integer part of the square root,
the current result squared (6839² = 46771921) must be the
largest perfect square smaller than 46785899. Why? The square root of
46785399 is going to be something like 6839.xxxx... This means
6839² is smaller than 46785399, but 6840² is
bigger than 46785399—the same thing as saying that 6839²
is the largest perfect square smaller than 46785399.
This idea is used later on to understand how the technique works, but
for now let's continue to generate more digits of the square root.
Similar to finding the fractional portion of the answer in
long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
, append two zeros to the remainder to get
the new remainder 1347800. The second column of the ninth row of the
square root bone is 18 and the current number on the board is 1366. So
compute
- 1366 + 1 → 1367 → append 8 → 13678
to set 13678 on the board.
The board and intermediate computations now look like this.
EWLINE
|
_____________ √46 78 53 99 = 6839. 36—10 78 10 24 ----- 54 53 40 89 ----- 13 64 99 12 30 21 -------- 1 34 78 00 |
The ninth row with 1231101 is the largest value smaller than the
remainder, so the first digit of the fractional part of the square
root is 9.
EWLINE
|
_____________ √46 78 53 99 = 6839.9 36—10 78 10 24 ----- 54 53 40 89 ----- 13 64 99 12 30 21 -------- 1 34 78 00 1 23 11 01 ---------- 11 66 99 |
Subtract the value of the ninth row from the remainder and append a
couple more zeros to get the new remainder 11669900. The second column
on the ninth row is 18 with 13678 on the board, so compute
- 13678 + 1 → 13679 → append 8 → 136798
and set 136798 on the board.
EWLINE
|
_____________ √46 78 53 99 = 6839.9 36—10 78 10 24 ----- 54 53 40 89 ----- 13 64 99 12 30 21 -------- 1 34 78 00 1 23 11 01 ---------- 11 66 99 00 |
You can continue these steps to find as many digits as you need and
you stop when you have the precision you want, or if you find that the
reminder becomes zero which means you have the exact square root.
Having found the desired number of digits, you can easily determine whether or not you need to round up; i.e., increment the last digit. You don't need to find another digit to see if it is equal to or greater than five. Simply append 25 to the root and compare that to the remainder; if it is less than or equal to the remainder, then the next digit will be at least five and round up is needed. In the example above, we see that 6839925 is less than 11669900, so we need to round up the root to 6840.0.
There's only one more trick left to describe. If you want to find the
square root of a number that isn't an integer, say 54782.917.
Everything is the same, except you start out by grouping the digits
to the left and right of the decimal point in groups of two.
That is, group 54782.917 as
- 5 47 82 . 91 7
and proceed to extract the square root from these groups of digits.
Diagonal modification
During the 19th century, Napier's bones underwent a transformation to make them easier to read. The rods began to be made with an angle of about 65° so that the triangles that had to be added were aligned vertically. In this case, in each square of the rod the unit is to the right and the ten (or the zero) to the left.
The rods were made such that the vertical and horizontal lines were more visible than the line where the rods touched, making the two components of each digit of the result much easier to read. Thus, in the picture it is immediately clear that:
- 987654321 × 5 = 4938271605
Genaille–Lucas rulers
In 1891, Henri Genaille invented a variant of Napier's bones which became known as Genaille–Lucas rulers. By representing the carry graphically, the user can read off the results of simple multiplication problems directly, with no intermediate mental calculations.The following example is calculating 52749 × 4 = 210996.
Card abacus
In addition to the previously-described "bones" abacus, Napier also constructed a card abacus. Both devices are reunited in a piece held by the SpanishSpain
Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...
National Archaeological Museum
National Archaeological Museum of Spain
The National Archaeological Museum of Spain is a museum in Madrid, Spain, located beside the Plaza de Colón , sharing its building with the National Library....
, in Madrid
Madrid
Madrid is the capital and largest city of Spain. The population of the city is roughly 3.3 million and the entire population of the Madrid metropolitan area is calculated to be 6.271 million. It is the third largest city in the European Union, after London and Berlin, and its metropolitan...
.
The apparatus is a box of wood
Wood
Wood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression...
with inlays of bone
Bone
Bones are rigid organs that constitute part of the endoskeleton of vertebrates. They support, and protect the various organs of the body, produce red and white blood cells and store minerals. Bone tissue is a type of dense connective tissue...
. In the top section it contains the "bones" abacus, and in the bottom section is the card abacus. This card abacus consists of 300 stored cards in 30 drawers. One hundred of these cards are covered with numbers (referred to as the "number cards"). The remaining two hundred cards contain small triangular holes, which, when laid on top of the number cards, allow the user to see only certain numbers. By the capable positioning of these cards, multiplications can be made up to the limit of a number 100 digits in length, by another number 200 digits in length.
In addition, the doors of the box contain the first powers of the digits, the coefficients of the terms of the first powers of the binomial
Binomial
In algebra, a binomial is a polynomial with two terms —the sum of two monomials—often bound by parenthesis or brackets when operated upon...
and the numeric data of the regular polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
.
It is not known who was the author of this piece, nor if it is of Spanish origin or came from a foreigner, although it is probable that it originally belonged to the Spanish Academy of Mathematics
Spanish Royal Academy of Sciences
The Spanish Royal Academy of Sciences was founded in 1847.-History:...
(which was created by Philip II
Philip II of Spain
Philip II was King of Spain, Portugal, Naples, Sicily, and, while married to Mary I, King of England and Ireland. He was lord of the Seventeen Provinces from 1556 until 1581, holding various titles for the individual territories such as duke or count....
) or was a gift from the Prince of Wales
Prince of Wales
Prince of Wales is a title traditionally granted to the heir apparent to the reigning monarch of the United Kingdom of Great Britain and Northern Ireland and the 15 other independent Commonwealth realms...
. The only thing that is sure is that it was conserved in the Palace, of where it was passed to the National library
Biblioteca Nacional de España
The Biblioteca Nacional de España is a major public library, the largest in Spain.It is located in Madrid, on the Paseo de Recoletos.-History:...
and later to the National Archaeological Museum, where it is still conserved.
In 1876, the Spanish government sent the apparatus to the exhibition of scientific instruments celebrated in Kensington
Kensington
Kensington is a district of west and central London, England within the Royal Borough of Kensington and Chelsea. An affluent and densely-populated area, its commercial heart is Kensington High Street, and it contains the well-known museum district of South Kensington.To the north, Kensington is...
, where it received much attention, up to the point at which several societies consulted the Spanish representation about the origin and use of the apparatus. This motivated D. Felipe Picatoste to write a monograph, that was sent to all the nations, in which he expressed surprise about the fact that the abacus was only well-known in "England
England
England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...
, country of origin of its inventor" (though of course he originated in Scotland
Scotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
).
External links
- Java implementation of Napier bones in various number systems at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Napier and other bones and many calculators

