
Nambu-Goto action
Encyclopedia
The Nambu–Goto action is the simplest invariant action
in bosonic string theory
, and is also used in other theories that investigate string-like objects (for example, cosmic strings
). It is the starting point of the analysis of zero-thickness (infinitely thin) string behavior, using the principles of Lagrangian mechanics
. Just as the action for a free point particle is proportional to its proper time
—i.e., the "length" of its world-line—a relativistic string's action is proportional to the area of the sheet which the string traces as it travels through spacetime.
It is named after Japanese physicists Yoichiro Nambu
and Tetsuo Goto.
, a mathematical relationship which takes an entire path and produces a single number. The physical path, that which the object actually follows, is the path for which the action is "stationary": any small variation of the path from the physical one does not significantly change the action. (Often, this is equivalent to saying the physical path is the one for which the action is a minimum.) Actions are typically written using Lagrangians, formulas which depend upon the object's state at a particular point in space and/or time. In non-relativistic mechanics, for example, a point particle's Lagrangian is the difference between kinetic and potential energy: L = K − U. The action, often written S, is then the integral of this quantity from a starting time to an ending time:
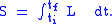
(Typically, when using Lagrangians, we assume we know the particle's starting and ending positions, and we concern ourselves with the path which the particle travels between those positions.)
This approach to mechanics has the advantage that it is easily extended and generalized. For example, we can write a Lagrangian for a relativistic
particle, which will be valid even if the particle is traveling close to the speed of light. To preserve Lorentz invariance, the action should only depend upon quantities that are the same for all Lorentz observers. The simplest such quantity is the proper time, the time measured by a clock carried by the particle. According to special relativity, all Lorentz observers watching a particle move will compute the same value for the quantity
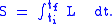
and ds/c is then an infinitesimal proper time. For a point particle not subject to external forces (i.e., one undergoing inertial motion), the relativistic action is
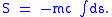
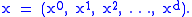
We describe a string using functions which map a position in the parameter space (τ, σ) to a point in spacetime. For each value of τ and σ, these functions specify a unique spacetime vector:
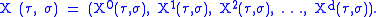
The functions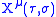 determine the shape which the world-sheet takes. Different Lorentz observers will disagree on the coordinates they assign to particular points on the world-sheet, but they must all agree on the total area which the world-sheet has. The Nambu–Goto action is chosen to be proportional to this total area.
determine the shape which the world-sheet takes. Different Lorentz observers will disagree on the coordinates they assign to particular points on the world-sheet, but they must all agree on the total area which the world-sheet has. The Nambu–Goto action is chosen to be proportional to this total area.
Let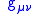 be the metric on the (d+1)-dimensional spacetime. Then,
be the metric on the (d+1)-dimensional spacetime. Then,
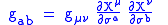
is the metric induced
on the string world-sheet.
The area
 of the world-sheet is given by:
of the world-sheet is given by:
where and
and 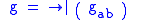
Using the notation that: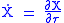
and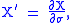
one can rewrite the metric
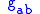 :
: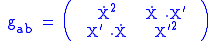

the Nambu–Goto action is defined as,
The factors before the integral give the action the correct units, energy multiplied by time. T0 is the tension in the string, and c is the speed of light. Typically, string theorists work in "natural units" where c is set to 1 (along with Planck's constant and Newton's constant G). Also, partly for historical reasons, they use the "slope parameter"
and Newton's constant G). Also, partly for historical reasons, they use the "slope parameter" 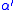 instead of T0. With these changes, the Nambu–Goto action becomes
instead of T0. With these changes, the Nambu–Goto action becomes
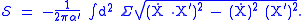
These two forms are, of course, entirely equivalent: choosing one over the other is a matter of convention and convenience.
Two further equivalent forms are
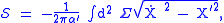
and
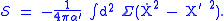
Typically, the Nambu–Goto action does not describe the correct quantum physics of strings. For this it must be modified
in a similar way as the action of a point particle. That is classically equal to minus mass times the invariant length in spacetime,
but must be replaced by a quadratic expression with the same classical value. Only then is the correct quantum physics obtained
.
For strings the analog correction is provided by the Polyakov action
, which is classically equivalent to the Nambu–Goto action, but gives the correct
quantum theory. It is, however, possible to develop a quantum theory from the Nambu-Goto action in the light-cone gauge.
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
in bosonic string theory
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
, and is also used in other theories that investigate string-like objects (for example, cosmic strings
Cosmic string
Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking is not simply connected. It is expected that at least one string...
). It is the starting point of the analysis of zero-thickness (infinitely thin) string behavior, using the principles of Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. Just as the action for a free point particle is proportional to its proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
—i.e., the "length" of its world-line—a relativistic string's action is proportional to the area of the sheet which the string traces as it travels through spacetime.
It is named after Japanese physicists Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
and Tetsuo Goto.
Relativistic Lagrangian mechanics
The basic principle of Lagrangian mechanics is that an object subjected to outside influences will "choose" a path which makes a certain quantity, the action, a minimum. The action is a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, a mathematical relationship which takes an entire path and produces a single number. The physical path, that which the object actually follows, is the path for which the action is "stationary": any small variation of the path from the physical one does not significantly change the action. (Often, this is equivalent to saying the physical path is the one for which the action is a minimum.) Actions are typically written using Lagrangians, formulas which depend upon the object's state at a particular point in space and/or time. In non-relativistic mechanics, for example, a point particle's Lagrangian is the difference between kinetic and potential energy: L = K − U. The action, often written S, is then the integral of this quantity from a starting time to an ending time:
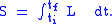
(Typically, when using Lagrangians, we assume we know the particle's starting and ending positions, and we concern ourselves with the path which the particle travels between those positions.)
This approach to mechanics has the advantage that it is easily extended and generalized. For example, we can write a Lagrangian for a relativistic
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
particle, which will be valid even if the particle is traveling close to the speed of light. To preserve Lorentz invariance, the action should only depend upon quantities that are the same for all Lorentz observers. The simplest such quantity is the proper time, the time measured by a clock carried by the particle. According to special relativity, all Lorentz observers watching a particle move will compute the same value for the quantity
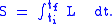
and ds/c is then an infinitesimal proper time. For a point particle not subject to external forces (i.e., one undergoing inertial motion), the relativistic action is
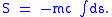
World-sheets
Just as a zero-dimensional point traces out a world-line on a spacetime diagram, a one-dimensional string is represented by a world-sheet. All world-sheets are two-dimensional surfaces, and we require two parameters to specify a point on the sheet. String theorists use the symbols τ and σ for these parameters. As it turns out, string theories involve higher-dimensional spaces than the 3D world with which we are familiar; bosonic string theory requires 25 spatial dimensions and one time axis. If d is the number of spatial dimensions, we can represent a point by the vector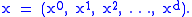
We describe a string using functions which map a position in the parameter space (τ, σ) to a point in spacetime. For each value of τ and σ, these functions specify a unique spacetime vector:
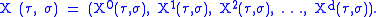
The functions
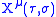 determine the shape which the world-sheet takes. Different Lorentz observers will disagree on the coordinates they assign to particular points on the world-sheet, but they must all agree on the total area which the world-sheet has. The Nambu–Goto action is chosen to be proportional to this total area.
determine the shape which the world-sheet takes. Different Lorentz observers will disagree on the coordinates they assign to particular points on the world-sheet, but they must all agree on the total area which the world-sheet has. The Nambu–Goto action is chosen to be proportional to this total area.Let
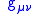 be the metric on the (d+1)-dimensional spacetime. Then,
be the metric on the (d+1)-dimensional spacetime. Then,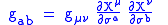
is the metric induced
Induced metric
In mathematics and theoretical physics, the induced metric is the metric tensor defined on a submanifold which is calculated from the metric tensor on a larger manifold into which the submanifold is embedded...
on the string world-sheet.
The area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
 of the world-sheet is given by:
of the world-sheet is given by:
where
 and
and 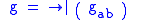
Using the notation that:
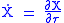
and
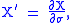
one can rewrite the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
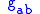 :
: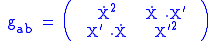

the Nambu–Goto action is defined as,
 |
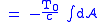 |
 |
 |
The factors before the integral give the action the correct units, energy multiplied by time. T0 is the tension in the string, and c is the speed of light. Typically, string theorists work in "natural units" where c is set to 1 (along with Planck's constant
 and Newton's constant G). Also, partly for historical reasons, they use the "slope parameter"
and Newton's constant G). Also, partly for historical reasons, they use the "slope parameter" 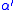 instead of T0. With these changes, the Nambu–Goto action becomes
instead of T0. With these changes, the Nambu–Goto action becomes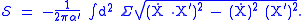
These two forms are, of course, entirely equivalent: choosing one over the other is a matter of convention and convenience.
Two further equivalent forms are
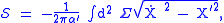
and
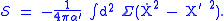
Typically, the Nambu–Goto action does not describe the correct quantum physics of strings. For this it must be modified
in a similar way as the action of a point particle. That is classically equal to minus mass times the invariant length in spacetime,
but must be replaced by a quadratic expression with the same classical value. Only then is the correct quantum physics obtained
.
For strings the analog correction is provided by the Polyakov action
Polyakov action
In physics, the Polyakov action is the two-dimensional action of a conformal field theory describing the worldsheet of a string in string theory...
, which is classically equivalent to the Nambu–Goto action, but gives the correct
quantum theory. It is, however, possible to develop a quantum theory from the Nambu-Goto action in the light-cone gauge.
Literature
- Zwiebach, Barton, A First Course in String Theory. Cambridge University Press (2004). ISBN 0-521-83143-1. Errata available online.
- Ortin, Thomas, Gravity and Strings, Cambridge Monographs, Cambridge University Press (2004).

