
Möbius plane
Encyclopedia
A Möbius plane or inversive plane is a particular kind of plane geometry
, built upon some affine planes by adding one point, called the ideal point or point at infinity. In a Möbius plane straight lines are a special case of circles; they are the circles that pass through the ideal point. Möbius planes have a simple axiomatization by incidence
properties. Thus a Möbius plane is analogous to a projective plane
(where an entire line at infinity is added to an affine plane) but the purpose is different. The Möbius plane provides a natural setting for inversive geometry of two dimensions and for properties shared by lines and circles in an affine plane such as the real or complex affine plane.
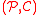 , and an incidence relation between them, satisfying the following four axioms. The elements of
, and an incidence relation between them, satisfying the following four axioms. The elements of  are called the points of M and the elements of
are called the points of M and the elements of  are the circles of M. If a point P and a circle C are incident we say "P is on C ", or "C is on P ". The intersection of two circles is the set of points on both. The axioms are: There exist four points not incident with any one circle. Any three points are incident with exactly one circle. Every circle is incident with at least three points. For any circle C, point P on C, and point Q not on C, there is a unique circle on both P and Q and having exactly one point of intersection with C.
are the circles of M. If a point P and a circle C are incident we say "P is on C ", or "C is on P ". The intersection of two circles is the set of points on both. The axioms are: There exist four points not incident with any one circle. Any three points are incident with exactly one circle. Every circle is incident with at least three points. For any circle C, point P on C, and point Q not on C, there is a unique circle on both P and Q and having exactly one point of intersection with C.
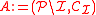 , where
, where 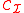 is the set of all circles on I. Then A is an affine plane in which a line is the set of nonideal points on a circle that contains I.
is the set of all circles on I. Then A is an affine plane in which a line is the set of nonideal points on a circle that contains I.
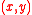 of a quadratic equation
of a quadratic equation 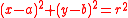 that has at least one solution. A characteristic of circles is that it takes three points to determine a circle, in contrast to the two points that determine a straight line. If we add one point I to A, which is on every straight line, and we call the extended lines "circles" along with the affine circles, then in the enlarged geometry it takes three points to determine any "circle", since two points of a line
that has at least one solution. A characteristic of circles is that it takes three points to determine a circle, in contrast to the two points that determine a straight line. If we add one point I to A, which is on every straight line, and we call the extended lines "circles" along with the affine circles, then in the enlarged geometry it takes three points to determine any "circle", since two points of a line 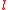 lie on many circles as well as on
lie on many circles as well as on 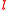 , so to single out
, so to single out 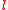 one must specify either a third affine point or the ideal point. Thus, the extended geometry is a Möbius plane, called the real or complex Möbius plane, M(R) or M(C).
one must specify either a third affine point or the ideal point. Thus, the extended geometry is a Möbius plane, called the real or complex Möbius plane, M(R) or M(C).
Conversely, given M(R) or M(C), by deleting any point P in it one gets the real or complex affine plane with its circle structure. Its lines are the circles of M that are on P (with P deleted) and its circles are the remaining circles of M. All such planes are isomorphic as incidence structures.
The real Möbius plane is one way of looking at the Riemann sphere
. Forgetting the complex structure of the Riemann sphere, rest the sphere on R2 so they are tangent at the south pole of the sphere and the origin of the plane. Under stereographic projection, the circles through the north pole correspond to straight lines and the other circles to plane circles. If we extend R2 by an ideal point to form a Möbius plane, the north pole projects to the ideal point, making the sphere a perfect model for M(R).
Not every Möbius plane is real or complex. Circles can be defined in the affine plane over any field and a Möbius plane constructed in an analogous manner.
Plane geometry
In mathematics, plane geometry may refer to:*Euclidean plane geometry, the geometry of plane figures,*geometry of a plane,or sometimes:*geometry of a projective plane, most commonly the real projective plane but possibly the complex projective plane, Fano plane or others;*geometry of the hyperbolic...
, built upon some affine planes by adding one point, called the ideal point or point at infinity. In a Möbius plane straight lines are a special case of circles; they are the circles that pass through the ideal point. Möbius planes have a simple axiomatization by incidence
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
properties. Thus a Möbius plane is analogous to a projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
(where an entire line at infinity is added to an affine plane) but the purpose is different. The Möbius plane provides a natural setting for inversive geometry of two dimensions and for properties shared by lines and circles in an affine plane such as the real or complex affine plane.
Abstract definition
A Möbius plane M is a pair of sets,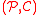 , and an incidence relation between them, satisfying the following four axioms. The elements of
, and an incidence relation between them, satisfying the following four axioms. The elements of  are called the points of M and the elements of
are called the points of M and the elements of  are the circles of M. If a point P and a circle C are incident we say "P is on C ", or "C is on P ". The intersection of two circles is the set of points on both. The axioms are: There exist four points not incident with any one circle. Any three points are incident with exactly one circle. Every circle is incident with at least three points. For any circle C, point P on C, and point Q not on C, there is a unique circle on both P and Q and having exactly one point of intersection with C.
are the circles of M. If a point P and a circle C are incident we say "P is on C ", or "C is on P ". The intersection of two circles is the set of points on both. The axioms are: There exist four points not incident with any one circle. Any three points are incident with exactly one circle. Every circle is incident with at least three points. For any circle C, point P on C, and point Q not on C, there is a unique circle on both P and Q and having exactly one point of intersection with C.Connection with affine planes
In an abstract Möbius plane M choose an arbitrary point I; call it the "ideal point". Let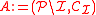 , where
, where 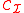 is the set of all circles on I. Then A is an affine plane in which a line is the set of nonideal points on a circle that contains I.
is the set of all circles on I. Then A is an affine plane in which a line is the set of nonideal points on a circle that contains I.Geometric constructions
In the real or complex affine plane, A = A(R) or A(C), a circle is the set of solutions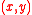 of a quadratic equation
of a quadratic equation 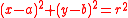 that has at least one solution. A characteristic of circles is that it takes three points to determine a circle, in contrast to the two points that determine a straight line. If we add one point I to A, which is on every straight line, and we call the extended lines "circles" along with the affine circles, then in the enlarged geometry it takes three points to determine any "circle", since two points of a line
that has at least one solution. A characteristic of circles is that it takes three points to determine a circle, in contrast to the two points that determine a straight line. If we add one point I to A, which is on every straight line, and we call the extended lines "circles" along with the affine circles, then in the enlarged geometry it takes three points to determine any "circle", since two points of a line 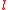 lie on many circles as well as on
lie on many circles as well as on 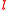 , so to single out
, so to single out 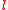 one must specify either a third affine point or the ideal point. Thus, the extended geometry is a Möbius plane, called the real or complex Möbius plane, M(R) or M(C).
one must specify either a third affine point or the ideal point. Thus, the extended geometry is a Möbius plane, called the real or complex Möbius plane, M(R) or M(C).Conversely, given M(R) or M(C), by deleting any point P in it one gets the real or complex affine plane with its circle structure. Its lines are the circles of M that are on P (with P deleted) and its circles are the remaining circles of M. All such planes are isomorphic as incidence structures.
The real Möbius plane is one way of looking at the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Forgetting the complex structure of the Riemann sphere, rest the sphere on R2 so they are tangent at the south pole of the sphere and the origin of the plane. Under stereographic projection, the circles through the north pole correspond to straight lines and the other circles to plane circles. If we extend R2 by an ideal point to form a Möbius plane, the north pole projects to the ideal point, making the sphere a perfect model for M(R).
Not every Möbius plane is real or complex. Circles can be defined in the affine plane over any field and a Möbius plane constructed in an analogous manner.
Inversion
Inversion in a circle of a Möbius plane M is the generalization of reflection in a straight line in an affine plane. This explains the name "inversive plane".External links
- Michiel Hazewinkel, editor, Encyclopaedia of Mathematics, article "Möbius plane". Springer-Verlag, Berlin–Heidelberg–New York. ISBN 1-4020-0609-8

