
Modes of convergence
Encyclopedia
In mathematics
, there are many senses in which a sequence or a series is said to be convergent. This article describes various modes (senses or species) of convergence in the settings where they are defined. For a list of modes of convergence, see Modes of convergence (annotated index)
Note that each of the following objects is a special case of the types preceding it: sets, topological spaces, uniform spaces, TAGs
(topological abelian groups), normed spaces
, Euclidean spaces, and the real/complex numbers. Also, note that any metric space
is a uniform space.
in first-countable space
s. Net
s are a generalization of sequences that is useful in spaces which are not first countable. Filter
s further generalize the concept of convergence.
In metric spaces, one can define Cauchy sequence
s. Cauchy nets and filters are generalizations to uniform space
s. Even more generally, Cauchy space
s are spaces in which Cauchy filters may be defined. Convergence implies "Cauchy-convergence", and Cauchy-convergence, together with the existence of a convergent subsequence implies convergence. The concept of completeness of metric spaces, and its generalizations is defined in terms of Cauchy sequences.
, convergence of a series
is defined as convergence of the sequence of partial sums. An important concept when considering series is unconditional convergence, which guarantees that the limit of the series is invariant under permutations of the summands.
In a normed vector space, one can define absolute convergence
as convergence of the series of norms (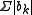 ). Absolute convergence implies Cauchy convergence of the sequence of partial sums (by the triangle inequality), which in turn implies absolute-convergence of some grouping (not reordering). The sequence of partial sums obtained by grouping is a subsequence of the partial sums of the original series. The norm convergence of absolutely convergent series is an equivalent condition for a normed linear space to be Banach
). Absolute convergence implies Cauchy convergence of the sequence of partial sums (by the triangle inequality), which in turn implies absolute-convergence of some grouping (not reordering). The sequence of partial sums obtained by grouping is a subsequence of the partial sums of the original series. The norm convergence of absolutely convergent series is an equivalent condition for a normed linear space to be Banach
(i.e.: complete).
Absolute convergence and convergence together imply unconditional convergence, but unconditional convergence does not imply absolute convergence in general, even if the space is Banach, although the implication holds in .
.
of the functions) is pointwise convergence
. It is defined as convergence of the sequence of values of the functions at every point. If the functions take their values in a uniform space, then one can define pointwise Cauchy convergence, uniform convergence, and uniform Cauchy convergence of the sequence.
Pointwise convergence implies pointwise Cauchy-convergence, and the converse holds if the space in which the functions take their values is complete. Uniform convergence implies pointwise convergence and uniform Cauchy convergence. Uniform Cauchy convergence and pointwise convergence of a subsequence imply uniform convergence of the sequence, and if the codomain is complete, then uniform Cauchy convergence implies uniform convergence.
If the domain of the functions is a topological space, local uniform convergence (i.e. uniform convergence on a neighborhood of each point) and compact (uniform) convergence
(i.e. uniform convergence on all compact subsets) may be defined. Note that "compact convergence" is always short for "compact uniform convergence," since "compact pointwise convergence" would mean the same thing as "pointwise convergence" (points are always compact).
Uniform convergence implies both local uniform convergence and compact convergence, since both are local notions while uniform convergence is global. If X is locally compact (even in the weakest sense: every point has compact neighborhood), then local uniform convergence is equivalent to compact (uniform) convergence. Roughly speaking, this is because "local" and "compact" connote the same thing.
For functions taking values in a normed linear space, absolute convergence refers to convergence of the series of positive, real-valued functions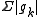 . "Pointwise absolute convergence" is then simply pointwise convergence of
. "Pointwise absolute convergence" is then simply pointwise convergence of 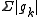 .
.
Normal convergence
http://eom.springer.de/N/n067430.htm is convergence of the series of non-negative real numbers obtained by taking the uniform (i.e. "sup") norm of each function in the series (uniform convergence of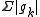 ). In Banach space
). In Banach space
s, pointwise absolute convergence implies pointwise convergence, and normal convergence implies uniform convergence.
For functions defined on a topological space, one can define (as above) local uniform convergence and compact (uniform) convergence
in terms of the partial sums of the series. If, in addition, the functions take values in a normed linear space, then local normal convergence (local, uniform, absolute convergence) and compact normal convergence (absolute convergence on compact sets).
Normal convergence implies both local normal convergence and compact normal convergence. And if the domain is locally compact (even in the weakest sense), then local normal convergence implies compact normal convergence.
s, then several modes of convergence that depend on measure-theoretic, rather than solely topological properties, arise. This includes pointwise convergence almost-everywhere, convergence in p-mean and convergence in measure. These are of particular interest in probability theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there are many senses in which a sequence or a series is said to be convergent. This article describes various modes (senses or species) of convergence in the settings where they are defined. For a list of modes of convergence, see Modes of convergence (annotated index)
Modes of convergence (annotated index)
The purpose of this article is to serve as an annotated index of various modes of convergence and their logical relationships. For an expository article, see Modes of convergence...
Note that each of the following objects is a special case of the types preceding it: sets, topological spaces, uniform spaces, TAGs
Topological abelian group
In mathematics, a topological abelian group, or TAG, is a topological group that is also an abelian group.That is, a TAG is both a group and a topological space, the group operations are continuous, and the group's binary operation is commutative....
(topological abelian groups), normed spaces
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
, Euclidean spaces, and the real/complex numbers. Also, note that any metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is a uniform space.
Elements of a topological space
Convergence can be defined in terms of sequencesLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
in first-countable space
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
s. Net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
s are a generalization of sequences that is useful in spaces which are not first countable. Filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
s further generalize the concept of convergence.
In metric spaces, one can define Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s. Cauchy nets and filters are generalizations to uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s. Even more generally, Cauchy space
Cauchy space
In general topology and analysis, a Cauchy space is a generalization of metric spaces and uniform spaces for which the notion of Cauchy convergence still makes sense. Cauchy spaces were introduced by H. H. Keller in 1968, as an axiomatic tool derived from the idea of a Cauchy filter, in order to...
s are spaces in which Cauchy filters may be defined. Convergence implies "Cauchy-convergence", and Cauchy-convergence, together with the existence of a convergent subsequence implies convergence. The concept of completeness of metric spaces, and its generalizations is defined in terms of Cauchy sequences.
Series of elements in a topological abelian group
In a topological abelian groupTopological abelian group
In mathematics, a topological abelian group, or TAG, is a topological group that is also an abelian group.That is, a TAG is both a group and a topological space, the group operations are continuous, and the group's binary operation is commutative....
, convergence of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
is defined as convergence of the sequence of partial sums. An important concept when considering series is unconditional convergence, which guarantees that the limit of the series is invariant under permutations of the summands.
In a normed vector space, one can define absolute convergence
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
as convergence of the series of norms (
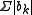 ). Absolute convergence implies Cauchy convergence of the sequence of partial sums (by the triangle inequality), which in turn implies absolute-convergence of some grouping (not reordering). The sequence of partial sums obtained by grouping is a subsequence of the partial sums of the original series. The norm convergence of absolutely convergent series is an equivalent condition for a normed linear space to be Banach
). Absolute convergence implies Cauchy convergence of the sequence of partial sums (by the triangle inequality), which in turn implies absolute-convergence of some grouping (not reordering). The sequence of partial sums obtained by grouping is a subsequence of the partial sums of the original series. The norm convergence of absolutely convergent series is an equivalent condition for a normed linear space to be BanachBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
(i.e.: complete).
Absolute convergence and convergence together imply unconditional convergence, but unconditional convergence does not imply absolute convergence in general, even if the space is Banach, although the implication holds in
 .
.Convergence of sequence of functions to a topological space
The most basic type of convergence for a sequence of functions (in particular, it does not assume any topological structure on the domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of the functions) is pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
. It is defined as convergence of the sequence of values of the functions at every point. If the functions take their values in a uniform space, then one can define pointwise Cauchy convergence, uniform convergence, and uniform Cauchy convergence of the sequence.
Pointwise convergence implies pointwise Cauchy-convergence, and the converse holds if the space in which the functions take their values is complete. Uniform convergence implies pointwise convergence and uniform Cauchy convergence. Uniform Cauchy convergence and pointwise convergence of a subsequence imply uniform convergence of the sequence, and if the codomain is complete, then uniform Cauchy convergence implies uniform convergence.
If the domain of the functions is a topological space, local uniform convergence (i.e. uniform convergence on a neighborhood of each point) and compact (uniform) convergence
Compact convergence
In mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
(i.e. uniform convergence on all compact subsets) may be defined. Note that "compact convergence" is always short for "compact uniform convergence," since "compact pointwise convergence" would mean the same thing as "pointwise convergence" (points are always compact).
Uniform convergence implies both local uniform convergence and compact convergence, since both are local notions while uniform convergence is global. If X is locally compact (even in the weakest sense: every point has compact neighborhood), then local uniform convergence is equivalent to compact (uniform) convergence. Roughly speaking, this is because "local" and "compact" connote the same thing.
Series of functions to a topological abelian group
Pointwise and uniform convergence of series of functions are defined in terms of convergence of the sequence of partial sums.For functions taking values in a normed linear space, absolute convergence refers to convergence of the series of positive, real-valued functions
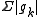 . "Pointwise absolute convergence" is then simply pointwise convergence of
. "Pointwise absolute convergence" is then simply pointwise convergence of 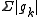 .
.Normal convergence
Normal convergence
In mathematics normal convergence is a type of convergence for series of functions. Like absolute-convergence, it has the useful property that it is preserved when the order of summation is changed.- History :...
http://eom.springer.de/N/n067430.htm is convergence of the series of non-negative real numbers obtained by taking the uniform (i.e. "sup") norm of each function in the series (uniform convergence of
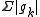 ). In Banach space
). In Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, pointwise absolute convergence implies pointwise convergence, and normal convergence implies uniform convergence.
For functions defined on a topological space, one can define (as above) local uniform convergence and compact (uniform) convergence
Compact convergence
In mathematics compact convergence is a type of convergence which generalizes the idea of uniform convergence. It is associated with the compact-open topology.-Definition:...
in terms of the partial sums of the series. If, in addition, the functions take values in a normed linear space, then local normal convergence (local, uniform, absolute convergence) and compact normal convergence (absolute convergence on compact sets).
Normal convergence implies both local normal convergence and compact normal convergence. And if the domain is locally compact (even in the weakest sense), then local normal convergence implies compact normal convergence.
Functions defined on a measure space
If one considers sequences of measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s, then several modes of convergence that depend on measure-theoretic, rather than solely topological properties, arise. This includes pointwise convergence almost-everywhere, convergence in p-mean and convergence in measure. These are of particular interest in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
.
See also
- Modes of convergence (annotated index)Modes of convergence (annotated index)The purpose of this article is to serve as an annotated index of various modes of convergence and their logical relationships. For an expository article, see Modes of convergence...
- Limit of a sequenceLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
- Net (mathematics)Net (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
- Filter (mathematics)Filter (mathematics)In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
- Convergence of random variablesConvergence of random variablesIn probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...

