Minkowski addition
Encyclopedia
In geometry
, the Minkowski sum (also known as dilation
) of two sets A and B in Euclidean space
is the result of adding every element of A to every element of B, i.e. the set
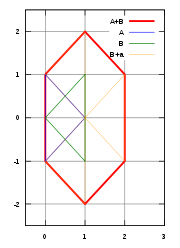
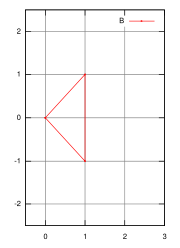
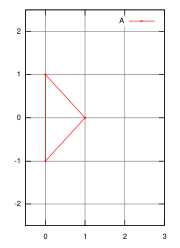
(triangle
s), with points represented by
and
then the Minkowski sum is
For Minkowski addition, the zero set, {0}, containing only the zero vector
, 0, has special importance
: For every non-empty subset, S, of a vector space
in algebraic terminology, the zero set, {0}, is the identity element
of Minkowski addition (on the collection of non-empty sets).
 In a real vector space, a non-empty
In a real vector space, a non-empty
set Q is defined to be convex
if, for each pair of its points, every point on the line segment
that joins them is a subset
of Q. For example, a solid disk, ●, is convex but a circle
, ○, is not, because it does not contain a line segment joining its points, ∅; the non-convex set of three integers, {0, 1, 2}, is contained in the interval, [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
shape, is non-convex. The empty set is convex, either by definition or vacuously
, depending on the author.
More formally, a set, Q, is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval
, [0, 1], the point
is a member of Q.
By mathematical induction
, a set, Q, is convex if and only if every convex combination
of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, …, vD} of a vector space is any weighted average, , for some indexed set of non-negative real numbers, {λd}, satisfying the equation = 1.
The definition of a convex set implies that the intersection
of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.
Minkowski addition behaves well with respect to the operation of taking convex hulls, as shown by the following proposition:
This result holds more generally for each finite collection of non-empty sets
In mathematical terminology, the operation
s of Minkowski summation and of forming convex hull
s are commuting
operations.
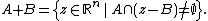
Thus, the essential Minkowski sum is defined by
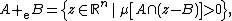
where μ denotes n-dimensional Lebesgue measure
. The reason for the term "essential" is the following property of indicator functions: while
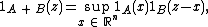
it can be seen that

where "ess sup" denotes the essential supremum.
. It arises in the brush-and-stroke paradigm of 2D computer graphics
(with various uses, notably by Donald E. Knuth in Metafont
), and as the solid sweep
operation of 3D computer graphics
.
of an object among obstacles. They are used for the computation of the configuration space
, which is the set of all admissible positions of the object. In the simple model of translational motion of an object in the plane, where the position of an object may be uniquely specified by the position of a fixed point of this object, the configuration space are the Minkowski sum of the set of obstacles and the movable object placed at the origin and rotated 180 degrees.
machining, the programming of the NC tool exploits the fact that the Minkowski sum of the cutting piece with its trajectory gives the shape of the cut in the material.
s P and Q in the plane with m and n vertices, their Minkowski sum is a convex polygon with at most m + n vertices and may be computed in time O (m + n) by a very simple procedure, which may be informally described as follows. Assume that the edges of a polygon are given and the direction, say, counterclockwise, along the polygon boundary. Then it is easily seen that these edges of the convex polygon are ordered by polar angle
. Let us merge the ordered sequences
of the directed edges from P and Q into a single ordered sequence S. Imagine that these edges are solid arrow
s which can be moved freely while keeping them parallel to their original direction. Assemble these arrows in the order of the sequence S by attaching the tail of the next arrow to the head of the previous arrow. It turns out that the resulting polygonal chain
will in fact be a convex polygon which is the Minkowski sum of P and Q.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Minkowski sum (also known as dilation
Dilation (morphology)
Dilation is one of the basic operations in mathematical morphology. Originally developed for binary images, it has been expanded first to grayscale images, and then to complete lattices...
) of two sets A and B in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is the result of adding every element of A to every element of B, i.e. the set



Example
For example, if we have two 2-simplicesSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
(triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s), with points represented by
- A = {(1, 0), (0, 1), (0, −1)}
and
- B = {(0, 0), (1, 1), (1, −1)},
then the Minkowski sum is
- A + B = {(1, 0), (2, 1), (2, −1), (0, 1), (1, 2), (1, 0), (0, −1), (1, 0), (1, −2)}, which looks like a hexagon, with three 'repeated' points at (1, 0).
For Minkowski addition, the zero set, {0}, containing only the zero vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
, 0, has special importance
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
: For every non-empty subset, S, of a vector space
- S + {0} = S;
in algebraic terminology, the zero set, {0}, is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of Minkowski addition (on the collection of non-empty sets).
Convex hulls of Minkowski sums

Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
set Q is defined to be convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
if, for each pair of its points, every point on the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
that joins them is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Q. For example, a solid disk, ●, is convex but a circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, ○, is not, because it does not contain a line segment joining its points, ∅; the non-convex set of three integers, {0, 1, 2}, is contained in the interval, [0, 2], which is convex. For example, a solid cube is convex; however, anything that is hollow or dented, for example, a crescent
Crescent
In art and symbolism, a crescent is generally the shape produced when a circular disk has a segment of another circle removed from its edge, so that what remains is a shape enclosed by two circular arcs of different diameters which intersect at two points .In astronomy, a crescent...
shape, is non-convex. The empty set is convex, either by definition or vacuously
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
, depending on the author.
More formally, a set, Q, is convex if, for all points v0 and v1 in Q and for every real number λ in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, [0, 1], the point
- (1 − λ) v0 + λv1
is a member of Q.
By mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, a set, Q, is convex if and only if every convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of members of Q also belongs to Q. By definition, a convex combination of an indexed subset {v0, v1, …, vD} of a vector space is any weighted average, , for some indexed set of non-negative real numbers, {λd}, satisfying the equation = 1.
The definition of a convex set implies that the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of two convex sets is a convex set. More generally, the intersection of a family of convex sets is a convex set. In particular, the intersection of two disjoint sets is the empty set, which is convex.
Minkowski addition behaves well with respect to the operation of taking convex hulls, as shown by the following proposition:
- For all subsets S1 and S2 of a real vector-space, the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of their Minkowski sum is the Minkowski sum of their convex hulls
- Conv(S1 + S2) = Conv(S1) + Conv(S2).
This result holds more generally for each finite collection of non-empty sets
- Conv(∑Sn) = ∑Conv(Sn).
In mathematical terminology, the operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s of Minkowski summation and of forming convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
s are commuting
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
operations.
Essential Minkowski sum
There is also a notion of the essential Minkowski sum +e of two subsets of Euclidean space. Note that the usual Minkowski sum can be written as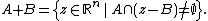
Thus, the essential Minkowski sum is defined by
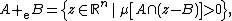
where μ denotes n-dimensional Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. The reason for the term "essential" is the following property of indicator functions: while
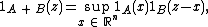
it can be seen that

where "ess sup" denotes the essential supremum.
Applications
Minkowski addition plays a central role in mathematical morphologyMathematical morphology
Mathematical morphology is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions...
. It arises in the brush-and-stroke paradigm of 2D computer graphics
2D computer graphics
2D computer graphics is the computer-based generation of digital images—mostly from two-dimensional models and by techniques specific to them...
(with various uses, notably by Donald E. Knuth in Metafont
METAFONT
Metafont is a programming language used to define vector fonts. It is also the name of the interpreter that executes Metafont code, generating the bitmap fonts that can be embedded into e.g. PostScript...
), and as the solid sweep
Solid sweep
The sweep Sw of a solid S is defined as the solid created when a motion M is applied to a given solid. The solid S should be considered to be a set of points in the Euclidean space R3. Then the solid Sw which is generated by sweeping S over M will contain all the points over which the points of S...
operation of 3D computer graphics
3D computer graphics
3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
.
Motion planning
Minkowski sums are used in motion planningMotion planning
Motion planning is a term used in robotics for the process of detailing a task into discrete motions....
of an object among obstacles. They are used for the computation of the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
, which is the set of all admissible positions of the object. In the simple model of translational motion of an object in the plane, where the position of an object may be uniquely specified by the position of a fixed point of this object, the configuration space are the Minkowski sum of the set of obstacles and the movable object placed at the origin and rotated 180 degrees.
Numerical control (NC) machining
In numerical controlNumerical control
Numerical control refers to the automation of machine tools that are operated by abstractly programmed commands encoded on a storage medium, as opposed to controlled manually via handwheels or levers, or mechanically automated via cams alone...
machining, the programming of the NC tool exploits the fact that the Minkowski sum of the cutting piece with its trajectory gives the shape of the cut in the material.
Algorithms for computing Minkowski sums
Two convex polygons in the plane
For two convex polygonConvex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
s P and Q in the plane with m and n vertices, their Minkowski sum is a convex polygon with at most m + n vertices and may be computed in time O (m + n) by a very simple procedure, which may be informally described as follows. Assume that the edges of a polygon are given and the direction, say, counterclockwise, along the polygon boundary. Then it is easily seen that these edges of the convex polygon are ordered by polar angle
Polar angle
In geometry, the polar angle may be* one of the two coordinates of a two-dimensional polar coordinate system;* one of the three coordinates of a three-dimensional spherical coordinate system; in this case it is also called the zenith....
. Let us merge the ordered sequences
Merge algorithm
Merge algorithms are a family of algorithms that run sequentially over multiple sorted lists, typically producing more sorted lists as output. This is well-suited for machines with tape drives...
of the directed edges from P and Q into a single ordered sequence S. Imagine that these edges are solid arrow
Arrow
An arrow is a shafted projectile that is shot with a bow. It predates recorded history and is common to most cultures.An arrow usually consists of a shaft with an arrowhead attached to the front end, with fletchings and a nock at the other.- History:...
s which can be moved freely while keeping them parallel to their original direction. Assemble these arrows in the order of the sequence S by attaching the tail of the next arrow to the head of the previous arrow. It turns out that the resulting polygonal chain
Polygonal chain
A polygonal chain, polygonal curve, polygonal path, or piecewise linear curve, is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points \scriptstyle called its vertices so that the curve consists of the line segments connecting the...
will in fact be a convex polygon which is the Minkowski sum of P and Q.
Other
If one polygon is convex and another one is not, the complexity of their Minkowski sum is O(nm). If both of them are nonconvex, their Minkowski sum complexity is O((mn)2).See also
- Interval arithmeticInterval arithmeticInterval arithmetic, interval mathematics, interval analysis, or interval computation, is a method developed by mathematicians since the 1950s and 1960s as an approach to putting bounds on rounding errors and measurement errors in mathematical computation and thus developing numerical methods that...
- Zonotope
- Parallel curve
- ErosionErosion (morphology)For use of "Erosion" in dermatopathology, see Erosion Erosion is one of two fundamental operations in Morphological image processing from which all other morphological operations are based...
- Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
External links
- Minkowski Sums, in Computational Geometry Algorithms Library
- The Minkowski Sum of Two Triangles and The Minkowski Sum of a Disk and a Polygon by George Beck, The Wolfram Demonstrations Project.
- Minkowski's addition of convex shapes by Alexander Bogomolny: an applet