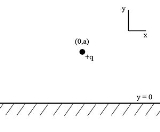
The method of image charges (also known as the method of images and method of mirror charges) is a basic problem-solving tool in electrostatics

Electrostatics

Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....

. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem (see Dirichlet boundary conditions or Neumann boundary conditions).
Any uniqueness theorem says that an object satisfying some set of given conditions or properties is the only such object that exists; it is uniquely determined by the specified conditions.

To illustrate, draw a closed loop to define a region inside and a surface on the line.