
Metabolic control analysis
Encyclopedia
Metabolic control analysis (MCA) is a mathematical framework for describing
metabolic
, signaling and genetic pathway
s. MCA quantifies how variables,
such as flux
es and species
concentrations, depend on network parameters.
In particular it is able to describe how network dependent properties,
called control coefficient
s, depend on local properties
called elasticities.
MCA was originally developed to describe the control in metabolic pathways
but was subsequently extended to describe signaling and genetic networks
. MCA has sometimes also been referred to as Metabolic Control Theory but this terminology was rather strongly opposed by Henrik Kacser
, one of the founders.
More recent work has shown that MCA can be mapped directly
on to classical control theory
and are as such equivalent.
Biochemical systems theory
is a similar formalism, though with a rather different objectives. Both are evolutions of an earlier theoretical analysis by Joseph Higgins.
change in a system variable, e.g. pathway flux (J) or metabolite concentration (S), in response to a relative change in a parameter
, e.g. enzyme activity
or the steady-state rate (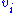 ) of step i. The two main control coefficients are the flux and concentration control coefficients. Flux control coefficients are defined by:
) of step i. The two main control coefficients are the flux and concentration control coefficients. Flux control coefficients are defined by:
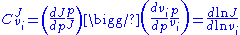
and concentration control coefficients by:
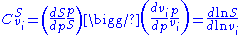
theorem was discovered independently by the Kacser/Burns group and the Heinrich/Rapoport group in the early 1970s and late 1960s. The flux control summation theorem implies that metabolic fluxes are systemic properties and that their control is shared by all reactions
in the system. When a single reaction changes its control of the flux this is compensated by changes in the control of the same flux by all other reactions.
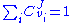
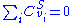
s.
theorems are specific relationships between elasticities and control coefficients. They are useful because they highlight the close relationship between the kinetic
properties of individual reactions and the system properties of a pathway. Two basic sets of theorems exists, one for flux and another for concentrations. The concentration connectivity theorems are divided again depending on whether the system species is different from the local species
is different from the local species 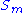 .
.
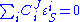
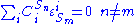

that relate the control coefficients to the elasticity coefficients. For example, consider the simplest non-trivial
pathway:
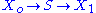
We assume that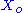 and
and 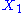 are fixed boundary species so that the pathway can reach a steady state. Let the first step have a rate
are fixed boundary species so that the pathway can reach a steady state. Let the first step have a rate 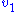 and the second step
and the second step 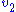 . Focusing on the flux control coefficients, we can write one summation and one connectivity theorem for this simple pathway:
. Focusing on the flux control coefficients, we can write one summation and one connectivity theorem for this simple pathway:
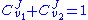

Using these two equations we can solve for the flux control coefficients to yield:
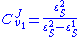
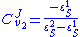
Using these equations we can look at some simple extreme behaviors. For example, let us assume that the first step is completely insensitive to its product (i.e. not reacting with it), S, then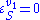 . In this case, the control coefficients reduce to:
. In this case, the control coefficients reduce to:
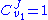
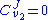
That is all the control (or sensitivity) is on the first step. This situation represents the classic rate-limiting step
that is frequently mentioned in text books. The flux through the pathway is completely dependent on the first step. Under these conditions, no other step in the pathway can affect the flux. The effect is however dependent on the complete insensitivity of the first step to its product. Such a situation is likely to be rare in real pathways. In fact the classic rate limiting step has almost never been observed experimentally. Instead, a range of limitingness is observed, with some steps having more limitingness (control) than others.
We can also derive the concentration control coefficients for the simple two step pathway:
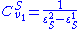
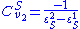
An alternative approach to deriving the control equations is to consider the perturbations
explicitly. Consider making a perturbation to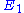 which changes the local rate
which changes the local rate 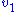 . The effect on the steady-state to a small change in
. The effect on the steady-state to a small change in 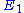 is to increase the flux and concentration of S. We can express these changes locally by describing the change in
is to increase the flux and concentration of S. We can express these changes locally by describing the change in 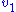 and
and 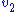 using the expressions:
using the expressions:

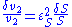
The local changes in rates are equal to the global changes in flux, J. In addition if we assume that the enzyme
elasticity of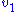 with respect to
with respect to 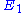 is unity, then
is unity, then
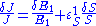
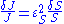
Dividing both sides by the fractional change in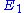 and taking the limit
and taking the limit
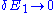 yields:
yields:
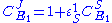
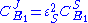
From these equations we can choose either to eliminate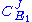 or
or 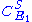 to yield the control equations given earlier. We can do the same kind of analysis for the second step to obtain the flux control coefficient for
to yield the control equations given earlier. We can do the same kind of analysis for the second step to obtain the flux control coefficient for 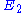 . Note that we have expressed the control coefficients relative to
. Note that we have expressed the control coefficients relative to  and
and 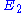 but if we assume that
but if we assume that 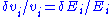 then the control coefficients can be written with respect to
then the control coefficients can be written with respect to 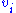 as before.
as before.

where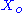 and
and 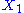 are fixed boundary species, the control equations for this pathway can be derived in a similar manner to the simple two step pathway although it is somewhat more tedious.
are fixed boundary species, the control equations for this pathway can be derived in a similar manner to the simple two step pathway although it is somewhat more tedious.
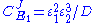
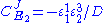
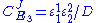
where D the denominator is given by:
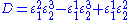
Note that every term in the numerator appears in the denominator, this ensures that the flux control coefficient summation theorem is satisfied.
Likewise the concentration control coefficients can also be derived, for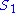
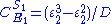
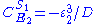
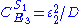
And for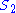
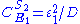

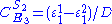
Note that the denominators remain the same as before and behave as a normalizing
factor.
metabolic
Metabolic pathway
In biochemistry, metabolic pathways are series of chemical reactions occurring within a cell. In each pathway, a principal chemical is modified by a series of chemical reactions. Enzymes catalyze these reactions, and often require dietary minerals, vitamins, and other cofactors in order to function...
, signaling and genetic pathway
Genetic pathway
A genetic pathway is the set of interactions occurring between a group of genes who depend on each other's individual functions in order to make the aggregate function of the network available to the cell...
s. MCA quantifies how variables,
such as flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es and species
Chemical species
Chemical species are atoms, molecules, molecular fragments, ions, etc., being subjected to a chemical process or to a measurement. Generally, a chemical species can be defined as an ensemble of chemically identical molecular entities that can explore the same set of molecular energy levels on a...
concentrations, depend on network parameters.
In particular it is able to describe how network dependent properties,
called control coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s, depend on local properties
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
called elasticities.
MCA was originally developed to describe the control in metabolic pathways
but was subsequently extended to describe signaling and genetic networks
Gene regulatory network
A gene regulatory network or genetic regulatory network is a collection of DNA segments in a cell whichinteract with each other indirectly and with other substances in the cell, thereby governing the rates at which genes in the network are transcribed into mRNA.In general, each mRNA molecule goes...
. MCA has sometimes also been referred to as Metabolic Control Theory but this terminology was rather strongly opposed by Henrik Kacser
Henrik Kacser
Henrik Kacser was an influential biochemist and geneticist. Henrik's achievements have been recognized by his election to the Royal Society of Edinburgh in 1990, by an Honorary Doctorate of the University of Bordeaux II in 1993.-Early life:Henrik Kacser was born in Romania in 1918 of...
, one of the founders.
More recent work has shown that MCA can be mapped directly
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
on to classical control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
and are as such equivalent.
Biochemical systems theory
Biochemical systems theory
Biochemical systems theory is a mathematical modelling framework for biochemical systems, based on ordinary differential equations , in which biochemical processes are represented using power-law expansions in the variables of the system....
is a similar formalism, though with a rather different objectives. Both are evolutions of an earlier theoretical analysis by Joseph Higgins.
Control Coefficients
A control coefficient measures the relative steady stateSteady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
change in a system variable, e.g. pathway flux (J) or metabolite concentration (S), in response to a relative change in a parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
, e.g. enzyme activity
Enzyme kinetics
Enzyme kinetics is the study of the chemical reactions that are catalysed by enzymes. In enzyme kinetics, the reaction rate is measured and the effects of varying the conditions of the reaction investigated...
or the steady-state rate (
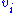 ) of step i. The two main control coefficients are the flux and concentration control coefficients. Flux control coefficients are defined by:
) of step i. The two main control coefficients are the flux and concentration control coefficients. Flux control coefficients are defined by: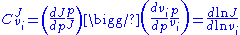
and concentration control coefficients by:
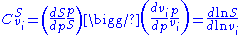
Summation Theorems
The flux control summationSummation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
theorem was discovered independently by the Kacser/Burns group and the Heinrich/Rapoport group in the early 1970s and late 1960s. The flux control summation theorem implies that metabolic fluxes are systemic properties and that their control is shared by all reactions
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
in the system. When a single reaction changes its control of the flux this is compensated by changes in the control of the same flux by all other reactions.
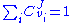
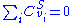
Elasticity Coefficients
The elasticity coefficient measures the local response of an enzyme or other chemical reaction to changes in its environment. Such changes include factors such as substrates, products or effector concentrations. For further information please refer to the dedicated page at Elasticity CoefficientElasticity Coefficient
Elasticity Coefficients are used in Physics, Economics, Chemistry, or more generally in mathematics as a definition of point elasticity: the article below applies to Chemical/Biochemical Elasticity Coefficients....
s.
Connectivity Theorems
The connectivityConnectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
theorems are specific relationships between elasticities and control coefficients. They are useful because they highlight the close relationship between the kinetic
Chemical kinetics
Chemical kinetics, also known as reaction kinetics, is the study of rates of chemical processes. Chemical kinetics includes investigations of how different experimental conditions can influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition...
properties of individual reactions and the system properties of a pathway. Two basic sets of theorems exists, one for flux and another for concentrations. The concentration connectivity theorems are divided again depending on whether the system species
 is different from the local species
is different from the local species  .
.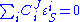
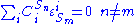

Control Equations
It is possible to combine the summation with the connectivity theorems to obtain closed expressionsClosed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
that relate the control coefficients to the elasticity coefficients. For example, consider the simplest non-trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
pathway:
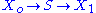
We assume that
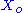 and
and 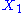 are fixed boundary species so that the pathway can reach a steady state. Let the first step have a rate
are fixed boundary species so that the pathway can reach a steady state. Let the first step have a rate 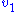 and the second step
and the second step 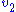 . Focusing on the flux control coefficients, we can write one summation and one connectivity theorem for this simple pathway:
. Focusing on the flux control coefficients, we can write one summation and one connectivity theorem for this simple pathway: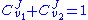

Using these two equations we can solve for the flux control coefficients to yield:
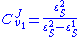
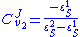
Using these equations we can look at some simple extreme behaviors. For example, let us assume that the first step is completely insensitive to its product (i.e. not reacting with it), S, then
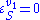 . In this case, the control coefficients reduce to:
. In this case, the control coefficients reduce to: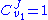
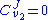
That is all the control (or sensitivity) is on the first step. This situation represents the classic rate-limiting step
Rate-determining step
The rate-determining step is a chemistry term for the slowest step in a chemical reaction. The rate-determining step is often compared to the neck of a funnel; the rate at which water flows through the funnel is determined by the width of the neck, not by the speed at which water is poured in. In...
that is frequently mentioned in text books. The flux through the pathway is completely dependent on the first step. Under these conditions, no other step in the pathway can affect the flux. The effect is however dependent on the complete insensitivity of the first step to its product. Such a situation is likely to be rare in real pathways. In fact the classic rate limiting step has almost never been observed experimentally. Instead, a range of limitingness is observed, with some steps having more limitingness (control) than others.
We can also derive the concentration control coefficients for the simple two step pathway:
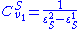
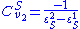
An alternative approach to deriving the control equations is to consider the perturbations
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
explicitly. Consider making a perturbation to
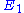 which changes the local rate
which changes the local rate 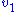 . The effect on the steady-state to a small change in
. The effect on the steady-state to a small change in 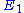 is to increase the flux and concentration of S. We can express these changes locally by describing the change in
is to increase the flux and concentration of S. We can express these changes locally by describing the change in 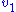 and
and 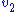 using the expressions:
using the expressions:
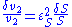
The local changes in rates are equal to the global changes in flux, J. In addition if we assume that the enzyme
Enzyme
Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...
elasticity of
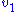 with respect to
with respect to 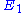 is unity, then
is unity, then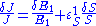
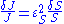
Dividing both sides by the fractional change in
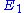 and taking the limit
and taking the limitLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
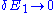 yields:
yields: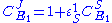
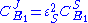
From these equations we can choose either to eliminate
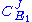 or
or 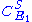 to yield the control equations given earlier. We can do the same kind of analysis for the second step to obtain the flux control coefficient for
to yield the control equations given earlier. We can do the same kind of analysis for the second step to obtain the flux control coefficient for 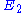 . Note that we have expressed the control coefficients relative to
. Note that we have expressed the control coefficients relative to  and
and 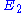 but if we assume that
but if we assume that 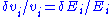 then the control coefficients can be written with respect to
then the control coefficients can be written with respect to 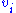 as before.
as before.Three Step Pathway
Consider the simple three step pathway:
where
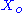 and
and 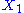 are fixed boundary species, the control equations for this pathway can be derived in a similar manner to the simple two step pathway although it is somewhat more tedious.
are fixed boundary species, the control equations for this pathway can be derived in a similar manner to the simple two step pathway although it is somewhat more tedious.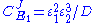
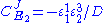
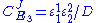
where D the denominator is given by:
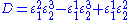
Note that every term in the numerator appears in the denominator, this ensures that the flux control coefficient summation theorem is satisfied.
Likewise the concentration control coefficients can also be derived, for
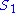
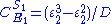
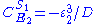
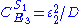
And for
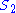
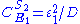

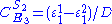
Note that the denominators remain the same as before and behave as a normalizing
Normalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
factor.

