
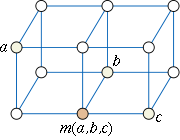
Median graph
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more specifically graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a median graph is an undirected graph in which any three vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
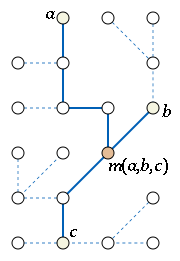
a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest paths between any two of a, b, and c.
The concept of median graphs has long been studied, for instance by or (more explicitly) by , but the first paper to call them "median graphs" appears to be . As Chung
Fan Chung
Fan Rong K Chung Graham , known professionally as Fan Chung, is a mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular...
, Graham
Ronald Graham
Ronald Lewis Graham is a mathematician credited by the American Mathematical Society as being "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years"...
, and Saks write, "median graphs arise naturally in the study of ordered sets and discrete distributive lattices, and have an extensive literature". In phylogenetics
Phylogenetics
In biology, phylogenetics is the study of evolutionary relatedness among groups of organisms , which is discovered through molecular sequencing data and morphological data matrices...
, the Buneman graph representing all maximum parsimony
Maximum parsimony
Parsimony is a non-parametric statistical method commonly used in computational phylogenetics for estimating phylogenies. Under parsimony, the preferred phylogenetic tree is the tree that requires the least evolutionary change to explain some observed data....
evolutionary trees
Phylogenetic tree
A phylogenetic tree or evolutionary tree is a branching diagram or "tree" showing the inferred evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical and/or genetic characteristics...
is a median graph. Median graphs also arise in social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
: if a set of alternatives has the structure of a median graph, it is possible to derive in an unambiguous way a majority preference among them.
Additional surveys of median graphs are given by , , and .
Examples
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
is a median graph. To see this, observe that in a tree, the union of the three shortest paths between any three vertices a, b, and c is either itself a path, or a subtree formed by three paths meeting at a single central node with degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
three. If the union of the three paths is itself a path, the median m(a,b,c) is equal to one of a, b, or c, whichever of these three vertices is between the other two in the path. If the subtree formed by the union of the three paths is not a path, the median of the three vertices is the central degree-three node of the subtree.
Additional examples of median graphs are provided by the grid graphs. In a grid graph, the coordinates of the median m(a,b,c) can be found as the median of the coordinates of a, b, and c. Conversely, it turns out that, in any median graph, one may label the vertices by points in an integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
in such a way that medians can be calculated coordinatewise in this way.
Squaregraph
In graph theory, a branch of mathematics, a squaregraph is a type of undirected graph that can be drawn in the plane in such a way that every bounded face is a quadrilateral and every vertex with three or fewer neighbors is incident to an unbounded face....
s, planar graphs in which all interior faces are quadrilaterals and all interior vertices have four or more incident edges, are another subclass of the median graphs. A polyomino
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
is a special case of a squaregraph and therefore also forms a median graph.
The simplex graph
Simplex graph
In graph theory, a branch of mathematics, the simplex graph κ of an undirected graph G is itself a graph, with one node for each clique in G...
κ(G) of any undirected graph G has a node for every clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
(complete subgraph) of G; two nodes are linked by an edge if the corresponding cliques differ by one vertex. The median of any three cliques may be formed by using the majority rule
Majority function
In Boolean logic, the majority function is a function from n inputs to one output. The value of the operation is false when n/2 or more arguments are false, and true otherwise....
to determine which vertices of the cliques to include; the simplex graph is a median graph in which this rule determines the median of any three vertices.
No cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
of length other than four can be a median graph, because any such cycle has three vertices a, b, and c such that the three shortest paths wrap all the way around the cycle without having a common intersection. For such a triple of vertices, there can be no median.
Equivalent definitions
In any graph, for any two vertices a and b, define the interval of vertices that lie on shortest paths- I(a,b) = {v | d(a,b) = d(a,v) + d(v,b)}.
A median graph is defined by the property that, for any three vertices a, b, and c, these intervals intersect in a single point:
- For all a, b, and c, |I(a,b) ∩ I(a,c) ∩ I(b,c)| = 1.
Equivalently, for every three vertices a, b, and c one can find a vertex m(a,b,c) such that the unweighted distances in the graph satisfy the equalities
- d(a,b) = d(a,m(a,b,c)) + d(m(a,b,c),b)
- d(a,c) = d(a,m(a,b,c)) + d(m(a,b,c),c)
- d(b,c) = d(b,m(a,b,c)) + d(m(a,b,c),c)
and m(a,b,c) is the only vertex for which this is true.
It is also possible to define median graphs as the solution sets of 2-satisfiability problems, as the retracts of hypercubes, as the graphs of finite median algebras, as the Buneman graphs of Helly split systems, and as the graphs of windex 2; see the sections below.
Distributive lattices and median algebras

Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
has a vertex for each lattice element and an edge for each pair of elements in the covering relation
Covering relation
In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours...
of the lattice. Lattices are commonly presented visually via Hasse diagram
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
s, which are drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
s of graphs of lattices. These graphs, especially in the case of distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s, turn out to be closely related to median graphs.
In a distributive lattice, Birkhoff's
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
self-dual ternary
Ternary operation
In mathematics, a ternary operation is an n-ary operation with n = 3. A ternary operation on a set A takes any given three elements of A and combines them to form a single element of A. An example of a ternary operation is the product in a heap....
median operation
- m(a,b,c) = (a ∧ b) ∨ (a ∧ c) ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c) ∧ (b ∨ c),
satisfies certain key axioms, which it shares with the usual median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of numbers in the range from 0 to 1 and with median algebra
Median algebra
In mathematics, a median algebra is a set with a ternary operation < x,y,z > satisfying a set of axioms which generalise the notion of median or majority function, as a Boolean function.The axioms are# < x,y,y > = y...
s more generally:
- IdempotenceIdempotenceIdempotence is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application...
: m(a,a,b) = a for any a and b. - CommutativityCommutativityIn mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
: m(a,b,c) = m(a,c,b) = m(b,a,c) = m(b,c,a) = m(c,a,b) = m(c,b,a) for any a, b, and c. - DistributivityDistributivityIn mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
: m(a,m(b,c,d),e) = m(m(a,b,e),c,m(a,d,e)) for all a, b, c, d, and e. - Identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
s: m(0,a,1) = a for all a.
The distributive law may be replaced by an associative law:
- AssociativityAssociativityIn mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
: m(x,w,m(y,w,z)) = m(m(x,w,y),w,z)
The median operation may also be used to define a notion of intervals for distributive lattices:
- I(a,b) = {x | m(a,x,b) = x} = {x | a ∧ b ≤ x ≤ a ∨ b}.
The graph of a finite distributive lattice has an edge between any two vertices a and b whenever I(a,b) = {a,b}. For any two vertices a and b of this graph, the interval I(a,b) defined in lattice-theoretic terms above consists of the vertices on shortest paths from a to b, and thus coincides with the graph-theoretic intervals defined earlier. For any a, b, and c, m(a,b,c) is the unique intersection of the three intervals I(a,b), I(a,c), and I(b,c). Therefore, the graph of any finite distributive lattice is a median graph. Conversely, if a median graph G contains two vertices 0 and 1 such that every other vertex lies on a shortest path between the two (equivalently, m(0,a,1) = a for all a), then we may define a distributive lattice in which a ∧ b = m(a,0,b) and a ∨ b = m(a,1,b), and G will be the graph of this lattice.
characterize graphs of distributive lattices directly as diameter-preserving retracts of hypercubes. More generally, any median graph gives rise to a ternary operation m satisfying idempotence, commutativity, and distributivity, but possibly without the identity elements of a distributive lattice. Any ternary operation on a finite set that satisfies these three properties (but that does not necessarily have 0 and 1 elements) gives rise in the same way to a median graph.
Convex sets and Helly families
In a median graph, a set S of vertices is said to be convex if, for every two vertices a and b belonging to S, the whole interval I(a,b) is a subset of S. Equivalently, given the two definitions of intervals above, S is convex if it contains every shortest path between two of its vertices, or if it contains the median of any three points at least two of which are from S. Observe that the intersection of any two convex sets is itself convex.The convex sets in a median graph have the Helly property: if F is any family of pairwise-intersecting convex sets, then all sets in F have a common intersection. For, if F has only three convex sets S, T, and U in it, with a in the intersection of the pair S and T, b in the intersection of the pair T and U, and c in the intersection of the pair S and U, then any shortest path from a to b must lie within T by convexity, and similarly any shortest path between the other two pairs of vertices must lie within the other two sets; but m(a,b,c) belongs to paths between all three pairs of vertices, so it lies within all three sets, and forms part of their common intersection. If F has more than three convex sets in it, the result follows by induction on the number of sets, for one may replace any two of the sets in F by their intersection, using the result for triples of sets to show that the replaced family is still pairwise intersecting.
A particularly important family of convex sets in a median graph, playing a role similar to that of halfspaces in Euclidean space, are the sets
- Wuv = {w | d(w,u) < d(w,v)}
defined for any edge uv of the graph. In words, Wuv consists of the vertices closer to u than to v, or equivalently the vertices w such that some shortest path from v to w goes through u.
To show that Wuv is convex, let w1w2...wk be any shortest path that starts and ends within Wuv; then w2 must also lie within Wuv, for otherwise the two points m1 = m(u,w1,wk) and m2 = m(m1,w2...wk) could be shown (by considering the possible distances between the vertices) to be distinct medians of u, w1, and wk, contradicting the definition of a median graph which requires medians to be unique. Thus, each successive vertex on a shortest path between two vertices of Wuv also lies within Wuv, so Wuv contains all shortest paths between its nodes, one of the definitions of convexity.
The Helly property for the sets Wuv plays a key role in the characterization of median graphs as the solution of 2-satisfiability instances, below.
2-satisfiability
Median graphs have a close connection to the solution sets of 2-satisfiability2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
problems that can be used both to characterize these graphs and to relate them to adjacency-preserving maps of hypercubes.
A 2-satisfiability instance consists of a collection of Boolean variables and a collection of clauses, constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
on certain pairs of variables requiring those two variables to avoid certain combinations of values. Usually such problems are expressed in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
, in which each clause is expressed as a disjunction and the whole set of constraints is expressed as a conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of clauses, such as
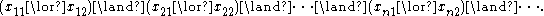
A solution to such an instance is an assignment of truth values to the variables that satisfies all the clauses, or equivalently that causes the conjunctive normal form expression for the instance to become true when the variable values are substituted into it. The family of all solutions has a natural structure as a median algebra, where the median of three solutions is formed by choosing each truth value to be the majority function
Majority function
In Boolean logic, the majority function is a function from n inputs to one output. The value of the operation is false when n/2 or more arguments are false, and true otherwise....
of the values in the three solutions; it is straightforward to verify that this median solution cannot violate any of the clauses. Thus, these solutions form a median graph, in which the neighbor of any solution is formed by negating a set of variables that are all constrained to be equal or unequal to each other.
Conversely, any median graph G may be represented in this way as the solution set to a 2-satisfiability instance. To find such a representation, create a 2-satisfiability instance in which each variable describes the orientation of one of the edges in the graph (an assignment of a direction to the edge causing the graph to become directed
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
rather than undirected) and each constraint allows two edges to share a pair of orientations only when there exists a vertex v such that both orientations lie along shortest paths from other vertices to v. Each vertex v of G corresponds to a solution to this 2-satisfiability instance in which all edges are directed towards v. Any
solution to the instance must come from some vertex v in this way, where v is the common intersection of the sets Wuw for edges directed from w to u; this common intersection exists due to the Helly property of the sets Wuw. Therefore, the solutions to this 2-satisfiability instance correspond one-for-one with the vertices of G.
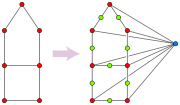
Retracts of hypercubes
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
φ from G to itself such that φ(v) = v for any vertex v in the subgraph φ(G). The image of the retraction is called a retract of G.
Retractions are examples of metric maps: the distance between φ(v) and φ(w), for any v and w, is at most equal to the distance between v and w, and is equal whenever v and w both belong to φ(G). Therefore, a retract must be an isometric subgraph of G: distances in the retract equal those in G.
If G is a median graph, and a, b, and c are any three vertices of a retract φ(G), then φ(m(a,b,c)) must be a median of a, b, and c, and so must equal m(a,b,c). Therefore, φ(G) contains medians of any triples of its vertices, and must also be a median graph. In other words, the family of median graphs is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the retraction operation.
A hypercube graph, in which the vertices correspond to all possible k-bit bitvectors and in which two vertices are adjacent when the corresponding bitvectors differ in only a single bit, is a special case of a k-dimensional grid graph and is therefore a median graph. The median of any three bitvectors a, b, and c may be calculated by computing, in each bit position, the majority function
Majority function
In Boolean logic, the majority function is a function from n inputs to one output. The value of the operation is false when n/2 or more arguments are false, and true otherwise....
of the bits of a, b, and c. Since median graphs are closed under retraction, and include the hypercubes, every retract of a hypercube is a median graph.
Conversely, every median graph must be the retract of a hypercube. This may be seen from the connection, described above, between median graphs and 2-satisfiability: let G be the graph of solutions to a 2-satisfiability instance; without loss of generality this instance can be formulated in such a way that no two variables are always equal or always unequal in every solution. Then the space of all truth assignments to the variables of this instance forms a hypercube. For each clause, formed as the disjunction of two variables or their complements, in the 2-satisfiability instance, one can form a retraction of the hypercube in which truth assignments violating this clause are mapped to truth assignments in which both variables satisfy the clause, without changing the other variables in the truth assignment. The composition of the retractions formed in this way for each of the clauses gives a retraction of the hypercube onto the solution space of the instance, and therefore gives a representation of G as the retract of a hypercube. In particular, median graphs are isometric subgraphs of hypercubes, and are therefore partial cube
Partial cube
In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube...
s. However, not all partial cubes are median graphs; for instance, a six-vertex cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
is a partial cube but is not a median graph.
As describe, an isometric embedding of a median graph into a hypercube may be constructed in time O(m log n), where n and m are the numbers of vertices and edges of the graph respectively.
Triangle-free graphs and recognition algorithms
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
, both had been well studied when observed that, in some sense, they are computationally equivalent. Therefore, the best known time bound for testing whether a graph is triangle-free, O(m1.41), applies as well to testing whether a graph is a median graph, and any improvement in median graph testing algorithms would also lead to an improvement in algorithms for detecting triangles in graphs.
In one direction, suppose one is given as input a graph G, and must test whether G is triangle-free. From G, construct a new graph H having as vertices each set of zero, one, or two adjacent vertices of G. Two such sets are adjacent in H when they differ by exactly one vertex. An equivalent description of H is that it is formed by splitting each edge of G into a path of two edges, and adding a new vertex connected to all the original vertices of G. This graph H is by construction a partial cube, but it is a median graph only when G is triangle-free: if a, b, and c form a triangle in G, then {a,b}, {a,c}, and {b,c} have no median in H, for such a median would have to correspond to the set {a,b,c}, but sets of three or more vertices of G do not form vertices in H. Therefore, G is triangle-free if and only if H is a median graph. In the case that G is triangle-free, H is its simplex graph
Simplex graph
In graph theory, a branch of mathematics, the simplex graph κ of an undirected graph G is itself a graph, with one node for each clique in G...
. An algorithm to test efficiently whether H is a median graph could by this construction also be used to test whether G is triangle-free. This transformation preserves the computational complexity of the problem, for the size of H is proportional to that of G.
The reduction in the other direction, from triangle detection to median graph testing, is more involved and depends on the previous median graph recognition algorithm of , which tests several necessary conditions for median graphs in near-linear time. The key new step involves using a breadth first search to partition the graph into levels according to their distances from some arbitrarily chosen root vertex, forming a graph in each level in which two vertices are adjacent if they share a common neighbor in the previous level, and searching for triangles in these graphs. The median of any such triangle must be a common neighbor of the three triangle vertices; if this common neighbor does not exist, the graph is not a median graph. If all triangles found in this way have medians, and the previous algorithm finds that the graph satisfies all the other conditions for being a median graph, then it must actually be a median graph. Note that this algorithm requires, not just the ability to test whether a triangle exists, but a list of all triangles in the level graph. In arbitrary graphs, listing all triangles sometimes requires Ω(m3/2) time, as some graphs have that many triangles, however Hagauer et al. show that the number of triangles arising in the level graphs of their reduction is near-linear, allowing the Alon et al. fast matrix multiplication based technique for finding triangles to be used.
Evolutionary trees, Buneman graphs, and Helly split systems
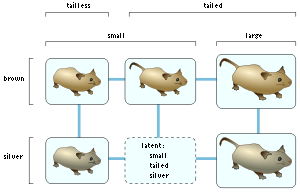
Species
In biology, a species is one of the basic units of biological classification and a taxonomic rank. A species is often defined as a group of organisms capable of interbreeding and producing fertile offspring. While in many cases this definition is adequate, more precise or differing measures are...
; such a tree must place the species at distinct vertices, and may have additional latent vertices, but the latent vertices are required to have three or more incident edges and must also be labeled with characteristics. A characteristic is binary when it has only two possible values, and a set of species and their characteristics exhibit perfect phylogeny
Perfect phylogeny
Perfect phylogeny is a term used in computational phylogenetics to denote a phylogenetic tree in which all internal nodes may be labeled as such that all characters evolve down the tree without homoplasy. That is, characteristics do not hold to evolutionary convergence, and do not have analogous...
when there exists an evolutionary tree in which the vertices (species and latent vertices) labeled with any particular characteristic value form a contiguous subtree. If a tree with perfect phylogeny is not possible, it is often desired to find one exhibiting maximum parsimony
Maximum parsimony
Parsimony is a non-parametric statistical method commonly used in computational phylogenetics for estimating phylogenies. Under parsimony, the preferred phylogenetic tree is the tree that requires the least evolutionary change to explain some observed data....
, or equivalently, minimizing the number of times the endpoints of a tree edge have different values for one of the characteristics, summed over all edges and all characteristics.
described a method for inferring perfect phylogenies for binary characteristics, when they exist. His method generalizes naturally to the construction of a median graph for any set of species and binary characteristics, which has been called the median network or Buneman graph and is a type of phylogenetic network
Phylogenetic network
A phylogenetic network is any graph used to visualize evolutionary relationships between nucleotide sequences, genes, chromosomes, genomes, or species . They are employed when reticulate events such as hybridization, horizontal gene transfer, recombination, or gene duplication and loss are...
s. Any maximum parsimony evolutionary tree embeds into the Buneman graph, in the sense that tree edges follow paths in the graph and the number of characteristic value changes on the tree edge is the same as the number in the corresponding path. The Buneman graph will be a tree if and only if a perfect phylogeny exists; this happens when there are no two incompatible characteristics for which all four combinations of characteristic values are observed.
To form the Buneman graph for a set of species and characteristics, first, eliminate redundant species that are indistinguishable from some other species and redundant characteristics that are always the same as some other characteristic. Then, form a latent vertex for every combination of characteristic values such that every two of the values exist in some known species. In the example shown, there are small brown tailless mice, small silver tailless mice, small brown tailed mice, large brown tailed mice, and large silver tailed mice; the Buneman graph method would form a latent vertex corresponding to an unknown species of small silver tailed mice, because every pairwise combination (small and silver, small and tailed, and silver and tailed) is observed in some other known species. However, the method would not infer the existence of large brown tailless mice, because no mice are known to have both the large and tailless traits. Once the latent vertices are determined, form an edge between every pair of species or latent vertices that differ in a single characteristic.
One can equivalently describe a collection of binary characteristics as a split system, a family of sets
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
having the property that the complement set of any set in the family is also in the family. This split system has a set for each characteristic value, consisting of the species that have that value. When the latent vertices are included, the resulting split system has the Helly property: any pairwise intersecting family of sets has a common intersection. In some sense median graphs are characterized as coming from Helly split systems: the pairs (Wuv, Wvu) defined for each edge uv of a median graph form a Helly split system, so if one applies the Buneman graph construction to this system no latent vertices will be needed and the result will be the same as the starting graph.
and describe techniques for simplified hand calculation of the Buneman graph, and use this construction to visualize human genetic relationships.
Additional properties
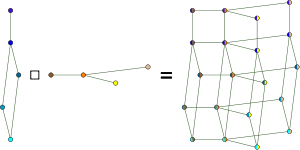
- The Cartesian productCartesian product of graphsIn graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
of any two median graphs is another median graph. Medians in the product graph may be computed by independently finding the medians in the two factors, just as medians in grid graphs may be computed by independently finding the median in each linear dimension.
- The windex of a graph measures the amount of lookaheadLookaheadLookahead is a tool in algorithms for looking ahead a few more input items before making a cost effective decision at one stage of the algorithm.- Lookahead in search problems :...
needed to optimally solve a problem in which one is given a sequence of graph vertices si, and must find as output another sequence of vertices ti minimizing the sum of the distances d(si,ti) and d(ti − 1,ti). Median graphs are exactly the graphs that have windex 2. In a median graph, the optimal choice is to set ti = m(ti − 1,si,si + 1).
- The property of having a unique median is also called the unique Steiner point property. An optimal Steiner treeSteiner treeThe Steiner tree problem, or the minimum Steiner tree problem, named after Jakob Steiner, is a problem in combinatorial optimization, which may be formulated in a number of settings, with the common part being that it is required to find the shortest interconnect for a given set of objects.The...
for any three vertices a, b, and c in a median graph may be found as the union of three shortest paths, from a, b, and c to m(a,b,c). study more generally the problem of finding the vertex minimizing the sum of distancesGeometric medianThe geometric median of a discrete set of sample points in a Euclidean space is the point minimizing the sum of distances to the sample points. This generalizes the median, which has the property of minimizing the sum of distances for one-dimensional data, and provides a central tendency in higher...
to each of a given set of vertices, and show that it has a unique solution for any odd number of vertices in a median graph. They also show that this median of a set S of vertices in a median graph satisfies the Condorcet criterionCondorcet criterionThe Condorcet candidate or Condorcet winner of an election is the candidate who, when compared with every other candidate, is preferred by more voters. Informally, the Condorcet winner is the person who would win a two-candidate election against each of the other candidates...
for the winner of an electionElectionAn election is a formal decision-making process by which a population chooses an individual to hold public office. Elections have been the usual mechanism by which modern representative democracy operates since the 17th century. Elections may fill offices in the legislature, sometimes in the...
: compared to any other vertex, it is closer to a majority of the vertices in S.
- As with partial cubes more generally, any median graph with n vertices has at most (n/2) log2 n edges. However, the number of edges cannot be too small: prove that in any median graph the inequality 2n − m − k ≤ 2 holds, where m is the number of edges and k is the dimension of the hypercube that the graph is a retract of. This inequality is an equality if and only if the median graph contains no cubes. This is a consequence of another identity for median graphs: the Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
Σ (-1)dim(Q) is always equal to one, where the sum is taken over all hypercube subgraphs Q of the given median graph.
- The only regularRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
median graphs are the hypercubes.
External links
- Median graphs, Information System for Graph Class Inclusions.
- Network, Free Phylogenetic Network Software. Network generates evolutionary trees and networks from genetic, linguistic, and other data.
- PhyloMurka, open-source software for median network computations from biological data.

