Mathematical finance
Encyclopedia
Mathematical finance is a field of applied mathematics
, concerned with financial markets. The subject has a close relationship with the discipline of financial economics
, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical
or numerical
models suggested by financial economics. Thus, for example, while a financial economist might study the structural reasons why a company may have a certain share price
, a financial mathematician may take the share price as a given, and attempt to use stochastic calculus
to obtain the fair value of derivative
s of the stock
(see: Valuation of options
).
In terms of practice, mathematical finance also overlaps heavily with the field of computational finance
(also known as financial engineering). Arguably, these are largely synonymous, although the latter focuses on application, while the former focuses on modeling and derivation (see: Quantitative analyst
), often by help of stochastic asset models. The fundamental theorem of arbitrage-free pricing
is one of the key theorems in mathematical finance. Many universities around the world now offer degree and research programs in mathematical finance; see Master of Mathematical Finance.
Once a fair price has been determined, the sell-side trader can make a market on the security. Therefore, derivatives pricing is a complex "extrapolation" exercise to define the current market value of a security, which is then used by the sell-side community.
Quantitative derivatives pricing was initiated by Louis Bachelier
in The Theory of Speculation (published 1900), with the introduction of the most basic and most influential of processes, the Brownian motion
, and its applications to the pricing of options. However, Bachelier's work hardly caught any attention outside academia.
The theory remained dormant until Fischer Black
and Myron Scholes
, along with fundamental contributions by Robert C. Merton
, applied the second most influential process, the geometric Brownian motion
, to option pricing. For this M. Scholes and R. Merton were awarded the 1997 Nobel Memorial Prize in Economic Sciences. Black was ineligible for the prize because of his death in 1995.
The next important step was the fundamental theorem of asset pricing by Harrison and Pliska (1981), according to which the suitably normalized current price P0 of a security is arbitrage-free, and thus truly fair, only if there exists a stochastic process Pt with constant expected value which describes its future evolution:
A process satisfying is called a "martingale". A martingale does not reward risk. Thus the probability of the normalized security price process is called "risk-neutral" and is typically denoted by the blackboard font
letter "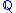
".
The relationship must hold for all times t: therefore the processes used for derivatives pricing are naturally set in continuous time.
The quants
who operate in the Q world of derivatives pricing are specialists with deep knowledge of the specific products they model.
Securities are priced individually, and thus the problems in the Q world are low-dimensional in nature.
Calibration is one of the main challenges of the Q world: once a continuous-time parametric process has been calibrated to a set of traded securities through a relationship such as (1), a similar relationship is used to define the price of new derivatives.
The main quantitative tools necessary to handle continuous-time Q-processes are Ito’s stochastic calculus
and partial differential equations (PDE’s).
This "real" probability distribution of the market prices is typically denoted by the blackboard font letter "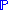
", as opposed to the "risk-neutral" probability "
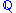" used in derivatives pricing.
Based on the P distribution, the buy-side community takes decisions on which securities to purchase in order to improve the prospective profit-and-loss profile of their positions considered as a portfolio.
The quantitative theory of risk and portfolio management started with the mean-variance framework
of Harry Markowitz
(1952), who caused a shift away from the concept of trying to identify the best individual stock for investment. Using a linear regression
strategy to understand and quantify the risk
(i.e. variance) and return
(i.e. mean) of an entire portfolio of stocks
, bonds
, and other securities, an optimization strategy was used to choose a portfolio with largest mean return subject to acceptable levels of variance in the return.
Next, breakthrough advances were made with the Capital Asset Pricing Model (CAPM) and the Arbitrage
Pricing Theory (APT) developed by Treynor (1962), Mossin (1966), William Sharpe
(1964), Lintner (1965) and Ross (1976).
For their pioneering work, Markowitz and Sharpe, along with Merton Miller, shared the 1990 Nobel Memorial Prize in Economic Sciences
, for the first time ever awarded for a work in finance.
The portfolio-selection work of Markowitz and Sharpe introduced mathematics to the “black art” of investment management.
With time, the mathematics has become more sophisticated. Thanks to Robert Merton and Paul Samuelson, one-period models were replaced by continuous time, Brownian-motion models
, and the quadratic utility function implicit in mean–variance optimization was replaced by more general increasing, concave utility functions.
Furthermore, in more recent years the focus shifted toward estimation risk, i.e., the dangers of incorrectly assuming that advanced time series analysis alone can provide completely accurate estimates of the market parameters
Contemporary practice of mathematical finance has been subjected to criticism from figures within the field notably by Nassim Nicholas Taleb in his book The Black Swan and Paul Wilmott
. Taleb claims that the prices of financial assets cannot be characterized by the simple models currently in use, rendering much of current practice at best irrelevant, and, at worst, dangerously misleading. Wilmott and Emanuel Derman
published the Financial Modelers' Manifesto in January 2008 which addresses some of the most serious concerns.
Bodies such as the Institute for New Economic Thinking
are now attempting to establish more effective theories and methods.
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, concerned with financial markets. The subject has a close relationship with the discipline of financial economics
Financial economics
Financial Economics is the branch of economics concerned with "the allocation and deployment of economic resources, both spatially and across time, in an uncertain environment"....
, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
or numerical
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
models suggested by financial economics. Thus, for example, while a financial economist might study the structural reasons why a company may have a certain share price
Share price
A share price is the price of a single share of a number of saleable stocks of a company. Once the stock is purchased, the owner becomes a shareholder of the company that issued the share.-Behavior of share prices:...
, a financial mathematician may take the share price as a given, and attempt to use stochastic calculus
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
to obtain the fair value of derivative
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
s of the stock
Stock
The capital stock of a business entity represents the original capital paid into or invested in the business by its founders. It serves as a security for the creditors of a business since it cannot be withdrawn to the detriment of the creditors...
(see: Valuation of options
Valuation of options
In finance, a price is paid or received for purchasing or selling options. This price can be split into two components.These are:* Intrinsic Value* Time Value-Intrinsic Value:...
).
In terms of practice, mathematical finance also overlaps heavily with the field of computational finance
Computational finance
Computational finance, also called financial engineering, is a cross-disciplinary field which relies on computational intelligence, mathematical finance, numerical methods and computer simulations to make trading, hedging and investment decisions, as well as facilitating the risk management of...
(also known as financial engineering). Arguably, these are largely synonymous, although the latter focuses on application, while the former focuses on modeling and derivation (see: Quantitative analyst
Quantitative analyst
A quantitative analyst is a person who works in finance using numerical or quantitative techniques. Similar work is done in most other modern industries, but the work is not always called quantitative analysis...
), often by help of stochastic asset models. The fundamental theorem of arbitrage-free pricing
Fundamental theorem of arbitrage-free pricing
The fundamental theorems of arbitrage/finance provide necessary and sufficient conditions for a market to be arbitrage free and for a market to be complete. An arbitrage opportunity is a way of making money with no initial investment without any possibility of loss...
is one of the key theorems in mathematical finance. Many universities around the world now offer degree and research programs in mathematical finance; see Master of Mathematical Finance.
History: Q versus P
There exist two separate branches of finance that require advanced quantitative techniques: derivatives pricing on the one hand, and risk and portfolio management on the other hand. One of the main differences is that they use different probabilities, namely the risk-neutral probability, denoted by "Q", and the actual probability, denoted by "P".Derivatives pricing: the Q world
The goal of derivatives pricing is to determine the fair price of a given security in terms of more liquid securities whose price is determined by the law of supply and demand. Examples of securities being priced are plain vanilla and exotic options, convertible bonds, etc.Once a fair price has been determined, the sell-side trader can make a market on the security. Therefore, derivatives pricing is a complex "extrapolation" exercise to define the current market value of a security, which is then used by the sell-side community.
| Goal | "extrapolate the present" |
| Environment | risk-neutral probability  |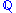
| Processes | continuous-time martingales |
| Dimension | low |
| Tools | Ito calculus, PDE’s |
| Challenges | calibration |
| Business | sell-side |
Quantitative derivatives pricing was initiated by Louis Bachelier
Louis Bachelier
-External links:** Louis Bachelier webpage at the Université de Franche-Comté, Besançon / France. Text in French.** also from Index Funds Advisors, this discussion of...
in The Theory of Speculation (published 1900), with the introduction of the most basic and most influential of processes, the Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, and its applications to the pricing of options. However, Bachelier's work hardly caught any attention outside academia.
The theory remained dormant until Fischer Black
Fischer Black
Fischer Sheffey Black was an American economist, best known as one of the authors of the famous Black–Scholes equation.-Background:...
and Myron Scholes
Myron Scholes
Myron Samuel Scholes is a Canadian-born American financial economist who is best known as one of the authors of the Black–Scholes equation. In 1997 he was awarded the Nobel Memorial Prize in Economic Sciences for a method to determine the value of derivatives...
, along with fundamental contributions by Robert C. Merton
Robert C. Merton
Robert Carhart Merton is an American economist, Nobel laureate in Economics, and professor at the MIT Sloan School of Management.-Biography:...
, applied the second most influential process, the geometric Brownian motion
Geometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
, to option pricing. For this M. Scholes and R. Merton were awarded the 1997 Nobel Memorial Prize in Economic Sciences. Black was ineligible for the prize because of his death in 1995.
The next important step was the fundamental theorem of asset pricing by Harrison and Pliska (1981), according to which the suitably normalized current price P0 of a security is arbitrage-free, and thus truly fair, only if there exists a stochastic process Pt with constant expected value which describes its future evolution:
A process satisfying is called a "martingale". A martingale does not reward risk. Thus the probability of the normalized security price process is called "risk-neutral" and is typically denoted by the blackboard font
Blackboard bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
letter "
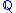". The relationship must hold for all times t: therefore the processes used for derivatives pricing are naturally set in continuous time.
The quants
Quantitative analyst
A quantitative analyst is a person who works in finance using numerical or quantitative techniques. Similar work is done in most other modern industries, but the work is not always called quantitative analysis...
who operate in the Q world of derivatives pricing are specialists with deep knowledge of the specific products they model.
Securities are priced individually, and thus the problems in the Q world are low-dimensional in nature.
Calibration is one of the main challenges of the Q world: once a continuous-time parametric process has been calibrated to a set of traded securities through a relationship such as (1), a similar relationship is used to define the price of new derivatives.
The main quantitative tools necessary to handle continuous-time Q-processes are Ito’s stochastic calculus
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
and partial differential equations (PDE’s).
Risk and portfolio management: the P world
Risk and portfolio management aims at modelling the probability distribution of the market prices of all the securities at a given future investment horizon.This "real" probability distribution of the market prices is typically denoted by the blackboard font letter "
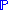", as opposed to the "risk-neutral" probability "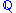" used in derivatives pricing.Based on the P distribution, the buy-side community takes decisions on which securities to purchase in order to improve the prospective profit-and-loss profile of their positions considered as a portfolio.
| Goal | "model the future" |
| Environment | real probability  |
| Processes | discrete-time series |
| Dimension | large |
| Tools | multivariate statistics |
| Challenges | estimation |
| Business | buy-side |
The quantitative theory of risk and portfolio management started with the mean-variance framework
Modern portfolio theory
Modern portfolio theory is a theory of investment which attempts to maximize portfolio expected return for a given amount of portfolio risk, or equivalently minimize risk for a given level of expected return, by carefully choosing the proportions of various assets...
of Harry Markowitz
Harry Markowitz
Harry Max Markowitz is an American economist and a recipient of the John von Neumann Theory Prize and the Nobel Memorial Prize in Economic Sciences....
(1952), who caused a shift away from the concept of trying to identify the best individual stock for investment. Using a linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
strategy to understand and quantify the risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
(i.e. variance) and return
Return
-In business, economics, and finance:* Rate of return, the financial term for the profit or loss derived from an investment* Tax return , various meanings relating to taxation...
(i.e. mean) of an entire portfolio of stocks
Stocks
Stocks are devices used in the medieval and colonial American times as a form of physical punishment involving public humiliation. The stocks partially immobilized its victims and they were often exposed in a public place such as the site of a market to the scorn of those who passed by...
, bonds
Bond (finance)
In finance, a bond is a debt security, in which the authorized issuer owes the holders a debt and, depending on the terms of the bond, is obliged to pay interest to use and/or to repay the principal at a later date, termed maturity...
, and other securities, an optimization strategy was used to choose a portfolio with largest mean return subject to acceptable levels of variance in the return.
Next, breakthrough advances were made with the Capital Asset Pricing Model (CAPM) and the Arbitrage
Pricing Theory (APT) developed by Treynor (1962), Mossin (1966), William Sharpe
William Forsyth Sharpe
William Forsyth Sharpe is the STANCO 25 Professor of Finance, Emeritus at Stanford University's Graduate School of Business and the winner of the 1990 Nobel Memorial Prize in Economic Sciences....
(1964), Lintner (1965) and Ross (1976).
For their pioneering work, Markowitz and Sharpe, along with Merton Miller, shared the 1990 Nobel Memorial Prize in Economic Sciences
Nobel Memorial Prize in Economic Sciences
The Nobel Memorial Prize in Economic Sciences, commonly referred to as the Nobel Prize in Economics, but officially the Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel , is an award for outstanding contributions to the field of economics, generally regarded as one of the...
, for the first time ever awarded for a work in finance.
The portfolio-selection work of Markowitz and Sharpe introduced mathematics to the “black art” of investment management.
With time, the mathematics has become more sophisticated. Thanks to Robert Merton and Paul Samuelson, one-period models were replaced by continuous time, Brownian-motion models
Brownian Model of Financial Markets
The Brownian motion models for financial markets are based on the work of Robert C. Merton and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William Sharpe, and are concerned with defining the concepts of financial assets and markets, portfolios, gains and...
, and the quadratic utility function implicit in mean–variance optimization was replaced by more general increasing, concave utility functions.
Furthermore, in more recent years the focus shifted toward estimation risk, i.e., the dangers of incorrectly assuming that advanced time series analysis alone can provide completely accurate estimates of the market parameters
Criticism
More sophisticated mathematical models and derivative pricing strategies were then developed but their credibility was damaged by the financial crisis of 2007–2010.Contemporary practice of mathematical finance has been subjected to criticism from figures within the field notably by Nassim Nicholas Taleb in his book The Black Swan and Paul Wilmott
Paul Wilmott
Paul Wilmott is a researcher, consultant and lecturer in quantitative finance. He is best known as the author of various academic and practitioner texts on risk and derivatives, and for Wilmott magazine and Wilmott.com , a quantitative finance portal....
. Taleb claims that the prices of financial assets cannot be characterized by the simple models currently in use, rendering much of current practice at best irrelevant, and, at worst, dangerously misleading. Wilmott and Emanuel Derman
Emanuel Derman
Emanuel Derman is a South African-born academic, businessman and writer. He is best known as a quantitative analyst, and author of the book My Life as A Quant: Reflections on Physics and Finance....
published the Financial Modelers' Manifesto in January 2008 which addresses some of the most serious concerns.
Bodies such as the Institute for New Economic Thinking
Institute for New Economic Thinking
The Institute for New Economic Thinking is a New York City-based nonprofit think tank founded in October 2009 with a $50 million pledge by George Soros as a result of the Financial crisis of 2007-2010.It has nobel laureates George Akerlof, Sir James Mirrlees, A...
are now attempting to establish more effective theories and methods.
See also
- Computational financeComputational financeComputational finance, also called financial engineering, is a cross-disciplinary field which relies on computational intelligence, mathematical finance, numerical methods and computer simulations to make trading, hedging and investment decisions, as well as facilitating the risk management of...
- Quantitative Behavioral FinanceQuantitative behavioral financeQuantitative behavioral finance is a new discipline that uses mathematical and statistical methodology to understand behavioral biases in conjunction with valuation. Some of this endeavor has been led by Gunduz Caginalp and collaborators including Vernon L...
- Derivative (finance)Derivative (finance)A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
, list of derivatives topics - Modeling and analysis of financial markets
- International Swaps and Derivatives AssociationInternational Swaps and Derivatives AssociationThe International Swaps and Derivatives Association is a trade organization of participants in the market for over-the-counter derivatives....
- Fundamental financial concepts - topics
- Model (economics)Model (economics)In economics, a model is a theoretical construct that represents economic processes by a set of variables and a set of logical and/or quantitative relationships between them. The economic model is a simplified framework designed to illustrate complex processes, often but not always using...
- List of finance topics
- List of economics topics, List of economists
- List of accounting topics
- Statistical FinanceStatistical financeStatistical finance, sometimes called econophysics, is an empirical attempt to shift finance from its normative roots to a positivist framework using exemplars from statistical physics with an emphasis on emergent or collective properties of financial markets...
- Brownian model of financial marketsBrownian Model of Financial MarketsThe Brownian motion models for financial markets are based on the work of Robert C. Merton and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William Sharpe, and are concerned with defining the concepts of financial assets and markets, portfolios, gains and...
- Master of Mathematical Finance