
Möbius strip
Encyclopedia

Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
. It can be realized as a ruled surface
Ruled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
. It was discovered independently by the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
and Johann Benedict Listing
Johann Benedict Listing
Johann Benedict Listing was a German mathematician.J. B. Listing was born in Frankfurt and died in Göttingen. He first introduced the term "topology", in a famous article published in 1847, although he had used the term in correspondence some years earlier...
in 1858.
A model can easily be created by taking a paper strip and giving it a half-twist, and then joining the ends of the strip together to form a loop. In Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
there are in fact two types of Möbius strips depending on the direction of the half-twist: clockwise and counterclockwise
Clockwise
Circular motion can occur in two possible directions. A clockwise motion is one that proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back to the top...
. That is to say, it is a chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
object with "handedness" (right-handed or left-handed).
It is straightforward to find algebraic equations
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
the solutions of which have the topology of a Möbius strip, but in general these equations do not describe the same geometric shape that one gets from the twisted paper model described above. In particular, the twisted paper model is a developable surface
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...
(it has zero Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
).
A system of differential-algebraic equations that describes models of this type
was published in 2007 together with its numerical solution.
The Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the Möbius strip is zero.
Properties
The Möbius strip has several curious properties. A line drawn starting from the seam down the middle will meet back at the seam but at the "other side". If continued the line will meet the starting point and will be double the length of the original strip. This single continuous curve demonstrates that the Möbius strip has only one boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
.
Cutting a Möbius strip along the center line yields one long strip with two full twists in it, rather than two separate strips; the result is not a Möbius strip. This happens because the original strip only has one edge which is twice as long as the original strip. Cutting creates a second independent edge, half of which was on each side of the scissors. Cutting this new, longer, strip down the middle creates two strips wound around each other, each with two full twists.
If the strip is cut along about a third of the way in from the edge, it creates two strips: One is a thinner Möbius strip — it is the center third of the original strip, comprising 1/3 of the width and the same length as the original strip. The other is a longer but thin strip with two full twists in it — this is a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of the edge of the original strip, and it comprises 1/3 of the width and twice the length of the original strip.
Other analogous strips can be obtained by similarly joining strips with two or more half-twists in them instead of one. For example, a strip with three half-twists, when divided lengthwise, becomes a strip tied in a trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
. (If this knot is unravelled, the strip is made with eight half-twists in addition to an overhand knot
Overhand knot
The overhand knot is one of the most fundamental knots and forms the basis of many others including the simple noose, overhand loop, angler's loop, reef knot, fisherman's knot and water knot. The overhand knot is very secure, to the point of jamming badly. It should be used if the knot is...
.) The equation for the number of half-twists after cutting a Mobius strip is 2N+2=M, where N is the number of half-twists before and M, the number after cutting a Möbius strip, giving it extra twists, and reconnecting the ends produces figures called paradromic rings.
A strip with an odd-number of half-twists, such as the Möbius strip, will have only one surface and one boundary. A strip twisted an even number of times will have two surfaces and two boundaries.
If a strip with an odd number of half-twists is cut in half along its length, it will result in a longer strip, with the same number of loops as there are half-twists in the original. Alternatively, if a strip with an even number of half-twists is cut in half along its length, it will result in two conjoined strips, each with the same number of twists as the original.
Geometry and topology
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is using the parametrization:


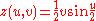
where and . This creates a Möbius strip of width 1 whose center circle has radius 1, lies in the xy plane and is centered at . The parameter u runs around the strip while v moves from one edge to the other.
In cylindrical polar coordinates , an unbounded version of the Möbius strip can be represented by the equation:
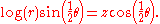
Topologically
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
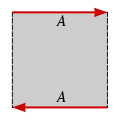
, the Möbius strip can be defined as the square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
with its top and bottom sides identified
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
by the relation for as in the diagram on the right.
A less used presentation of the Möbius strip is as the orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
quotient of a torus. A torus can be constructed as the square with the edges identified as (glue left to right) and (glue bottom to top). If one then also identified , then one obtains the Möbius strip. The diagonal of the square (the points (x,x) where both coordinates agree) becomes the boundary of the Möbius strip, and carries an orbifold structure, which geometrically corresponds to "reflection" – geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s (straight lines) in the Möbius strip reflect off the edge back into the strip. Notationally, this is written as T2/S2 – the 2-torus quotiented by the group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on two letters (switching coordinates), and it can be thought of as the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of two unordered points on the circle, possibly the same (the edge corresponds to the points being the same), with the torus corresponding to two ordered points on the circle.
The Möbius strip is a two-dimensional compact manifold (i.e. a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
) with boundary. It is a standard example of a surface which is not orientable. The Möbius strip is also a standard example used to illustrate the mathematical concept of a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
. Specifically, it is a nontrivial bundle over the circle S1 with a fiber the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
, I = [0,1]. Looking only at the edge of the Möbius strip gives a nontrivial two point (or Z2) bundle over S1.
A simple construction of the Möbius strip which can be used to portray it in computer graphics or modeling packages is as follows :
- Take a rectangular strip. Rotate it around a fixed point not in its plane. At every step also rotate the strip along a line in its plane (the line which divides the strip in two) and perpendicular to the main orbital radius. The surface generated on one complete revolution is the Möbius strip.
- Take a Möbius strip and cut it along the middle of the strip. This will form a new strip, which is a rectangle joined by rotating one end a whole turn. By cutting it down the middle again, this forms two interlocking whole-turn strips.
The open Möbius band
The open Möbius band is formed by deleting the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of the standard Möbius band. It is constructed from the set } by identifying (glueing) the points (0,y) and (1,1−y) for all
Occurrence and use in mathematics
The space of unoriented lines in the plane is diffeomorphic to the open Möbius band.To see why, notice that each line in the plane has an equation for fixed constants a, b and c. We can identify the equation with the point (a,b,c). However, the line given by is also given by for all .
These equations, which give the same line, are identified with the points (λa,λb,λc). Thus, the space of lines in the plane is a (proper) subset of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
; where the equation corresponds to the point (a:b:c) in homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. It is only a subset because some equations of the form do not give lines. We need to disallow to be sure that the equation does indeed give a line. The space of unoriented lines in the plane is given by deleting the point from the real projective plane. This space is exactly the open Möbius band.
Möbius band with flat edge
The edge of a Möbius strip is topologically equivalent to the circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. Under the usual embeddings of the strip in Euclidean space, as above, this edge is not an ordinary (flat) circle. It is possible to embed
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
a Möbius strip in three dimensions so that the edge is a circle. One way to think of this is to begin with a minimal Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
immersed in the 3-sphere and take half of it, which is an embedded Möbius band in 4-space; this figure M has been called the "Sudanese Möbius Band". (The name comes from a combination of the names of two topologists, Sue Goodman and Daniel Asimov). Applying stereographic projection to M puts it in 3-dimensional space, as can be seen here as well as in the pictures below. (Some have incorrectly labeled the stereographic image in 3-space "Sudanese", but this is rather an image of the actual Sudanese one, which has a high degree of symmetry as a Riemannian surface: its isometry group contains SO(2). A well-known parametrization of it follows.)
To see this, first consider such an embedding into the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
S3 regarded as a subset of R4. A parametrization for this embedding is given by {(z1(η,φ), z2(η,φ))}, where


Here we have used complex notation and regarded R4 as C2. The parameter η runs from 0 to π and φ runs from 0 to 2π. Since | z1 |2 + | z2 |2 = 1 the embedded surface lies entirely on S3. The boundary of the strip is given by | z2 | = 1 (corresponding to η = 0, π), which is clearly a circle on the 3-sphere.
To obtain an embedding of the Möbius strip in R3 one maps S3 to R3 via a stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. The projection point can be any point on S3 which does not lie on the embedded Möbius strip (this rules out all the usual projection points). Stereographic projections map circles to circles and will preserve the circular boundary of the strip. The result is a smooth embedding of the Möbius strip into R3 with a circular edge and no self-intersections.
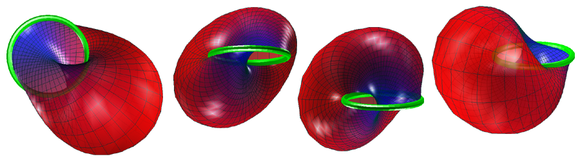
Related objects
A closely related 'strange' geometrical object is the Klein bottleKlein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
. A Klein bottle can be produced by gluing two Möbius strips together along their edges; this cannot be done in ordinary three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
without creating self-intersections.
Another closely related manifold is the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. If a circular disk is cut out of the real projective plane, what is left is a Möbius strip. Going in the other direction, if one glues a disk to a Möbius strip by identifying their boundaries, the result is the projective plane. In order to visualize this, it is helpful to deform the Möbius strip so that its boundary is an ordinary circle (see above). The real projective plane, like the Klein bottle, cannot be embedded in three-dimensions without self-intersections.
In graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Möbius ladder
Möbius ladder
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle...
is a cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
closely related to the Möbius strip.
Applications

Conveyor belt
A conveyor belt consists of two or more pulleys, with a continuous loop of material - the conveyor belt - that rotates about them. One or both of the pulleys are powered, moving the belt and the material on the belt forward. The powered pulley is called the drive pulley while the unpowered pulley...
s that last longer because the entire surface area of the belt gets the same amount of wear, and as continuous-loop recording tapes (to double the playing time). Möbius strips are common in the manufacture of fabric computer printer and typewriter ribbon
Typewriter ribbon
A typewriter ribbon is an expendable module serving the function of transferring pigment to paper in various devices for impact printing. Such ribbons were part of standard designs for hand- or motor-driven typewriters, teleprinters, stenotype machines, computer-driven printers and many mechanical...
s, as they allow the ribbon to be twice as wide as the print head while using both half-edges evenly.
A device called a Möbius resistor
Möbius resistor
A Möbius resistor is an electrical component made up of two conductive surfaces separated by a dielectric material, twisted 180° and connected to form a Möbius strip...
is an electronic circuit element that has the property of canceling its own inductive reactance. Nikola Tesla
Nikola Tesla
Nikola Tesla was a Serbian-American inventor, mechanical engineer, and electrical engineer...
patented similar technology in the early 1900s: "Coil for Electro Magnets" was intended for use with his system of global transmission of electricity without wires.
The Möbius strip is the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of two unordered points on a circle. Consequently, in music theory
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
, the space of all two note chords, known as dyads
Dyad (music)
In music, a dyad is a set of two notes or pitches. Although most chords have three or more notes, in certain contexts a dyad may be considered to be a chord. The most common two-note chord is made from the interval of a perfect fifth, which may be suggestive of music of the Medieval or Renaissance...
, takes the shape of a Möbius strip; this and generalizations to more points is a significant application of orbifolds to music theory.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
/electro-technology:
- as compact resonator with the resonance frequency which is half that of identically constructed linear coils
- as inductionless resistance
- as superconductors with high transition temperature
In chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
/nano-technology:
- as molecular knotMolecular knotIn chemistry, a molecular knot, or knotane, is a mechanically-interlocked molecular architecture that is analogous to a macroscopic knot. A molecular knot in a trefoil knot configuration is chiral, having at least two enantiomers. Examples of naturally formed knotanes are DNA and certain proteins....
s with special characteristics (Knotane [2], Chirality) - as molecular engines
- as graphene volume (nano-graphite) with new electronic characteristics, like helical magnetism
- in a special type of aromaticity: Möbius aromaticityMöbius aromaticityIn organic chemistry, Möbius aromaticity is a special type of aromaticity believed to exist in a number of organic molecules. In terms of MO theory these compounds have in common a monocyclic array of molecular orbitals in which there is an odd number of out-of-phase overlaps which reveals the...
- charged particles, which were caught in the magnetic field of the earth, can move on a Möbius band
- the cyclotide (cyclic protein) Kalata B1, active substance of the plant Oldenlandia affinis, contains Möbius topology for the peptide backbone.
External links
- Möbius Strip Video
- A virtual walk in the solar wind
- Animation of a rotating Sudanese Möbius band
- h2g2 - The Amazing Möbius Strip
- Johann Benedict Listing
- Knitted version
- Möbius Strip Music Box
- Möbius strip at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Science News 7/28/07: A Twist on the Möbius Band: Researchers work out the shape of a paper strip
- The Möbius Gear — A functional planetary gear model in which one gear is a Möbius strip
- Visualization of J. S. Bach's crab canon on a Möbius strip
- The protein with a topological twist
- Tridimensional and rotational möbius strip
- Huckel spectra of Mobius pi systems
- Beyond the Mobius Strip

